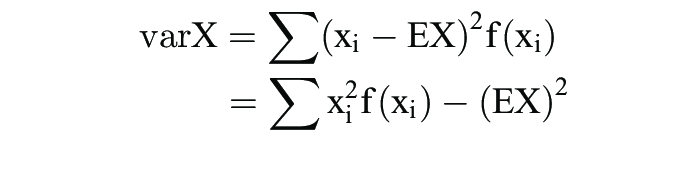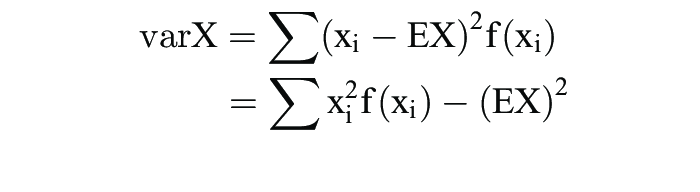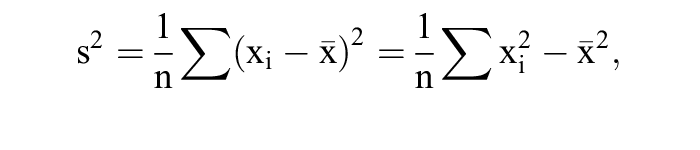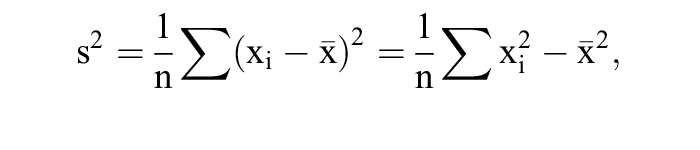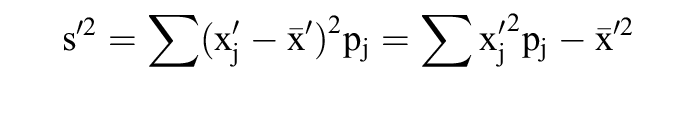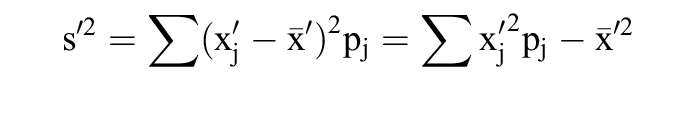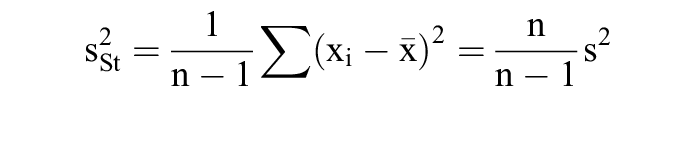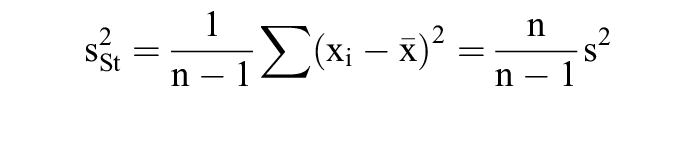Varianz

gebräuchlichste Maßzahl zur Charakterisierung der Streuung einer theoretischen oder empirischen Verteilung. Die Varianz ist ein nicht relativiertes Streuungsmaß.

1. Ist X eine Zufallsvariable, so bezeichnet

varX = E(X - EX)² = EX² - (EX)²

deren Varianz. Bei einer diskreten Zufallsvariablen mit den Ausprägungen x_i, der Wahrscheinlichkeitsfunktion f(x) und dem Erwartungswert EX ist die Varianz gemäß

zu ermitteln; analog ist bei stetigen Zufallsvariablen mittels Integration zu verfahren.

2. Liegen n Ausprägungen x_i eines metrischen Merkmals vor, so ist deren Varianz, berechnet aus den Urwerten,

wobei den Durchschnitt bezeichnet (arithmetisches Mittel).

3. Ist eine klassierte Verteilung gegeben, dann ist die Varianz exakt als Summe der internen Varianz (Binnenklassenvarianz) und der externen Varianz (Zwischenklassenvarianz) zu bestimmen (Varianzzerlegung). Stehen die interne und externe Varianz nicht zur Verfügung, so wird die Varianz oft unter Verwendung der Klassenmitten x'_j und der relativen Häufigkeiten p_j gemäß

approximativ bestimmt, wobei ' der analoge Näherungswert für das arithmetische Mittel ist. Diese Näherung tendiert zu einem zu niedrigen Ausweis der Varianz, da die interne Varianz mit 0 unterstellt wird.

4. Liegt ein Befund aus einem uneingeschränkten Zufallsstichprobenverfahren vor, dann wird die Stichproben-Varianz

als Schätzwert für die Varianz der Grundgesamtheit verwendet, weil sie bessere Schätzeigenschaften als s² aufweist (bes. Erwartungstreue). Zur einfacheren Berechnung der Varianz wird der Verschiebungssatz angewendet, der oben jeweils die zweite Formel ergibt.