Volatility Cone

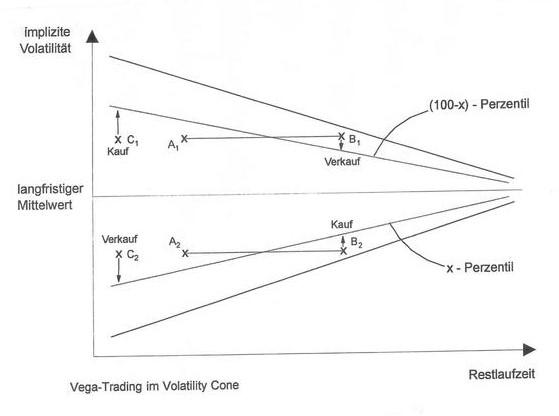
1. Begriff: kegelförmige Struktur der historischen Minima und Maxima der (tatsächlichen oder) impliziten Volatilität in Abhängigkeit von der Restlaufzeit der jeweiligen Optionen. Die Abbildung auf der nächsten Seite zeigt einen schematisierten Cone; zur angedeuteten Volatilitätsstrategie vgl. dortselbst, Ziff. 4.c).

Bild in Originalgröße zeigen

2. Erklärungsansätze: Nach h.M. kann ein Cone grundsätzlich in unmittelbarer Analogie zur Erwartungstheorie der Zinsstruktur erklärt werden: Ist die aktuelle kurzfristige implizite Volatilität hoch, wird im Sinne der (generell festzustellenden) Mean Reversion der Volatilität deren Rückgang in der Zukunft erwartet und als implizite Forward-Volatilität bereits heute in den längerfristigen impliziten Volatilitäten sichtbar und umgekehrt; dabei steigt die Wahrscheinlichkeit einer Mean Reversion mit zunehmendem Zeithorizont, der mit der Restlaufzeit der Optionen korrespondiert. Dies lässt sich inhaltlich darauf zurückführen, dass neue volatilitätsrelevante Informationen (Volatilitätsinnovationen) auf hinreichend informationseffizienten (gerade: Options-)Märkten kurzfristig verarbeitet werden und sich damit in der impliziten Volatilität von Kurzläufern relativ stärker niederschlagen als in der von Langläufern; während deren Restlaufzeit drängen nämlich erfahrungsgemäß immer wieder neue Informationen an den Markt. Plausibilisieren lässt sich dies damit, dass eine implizite Volatilität von At-the-Money (ATM)-Optionen exakt, ansonsten approximativ in der erwarteten Durchschnittsvolatilität über die Restlaufzeit besteht. Aus dem gleichen Grund ist die implizite Volatilität von Kurzläufern volatiler als die von Langläufern. Bei alldem ist keinerlei Aussage über die Prognosequalität der impliziten Forward-Volatilitäten für die zukünftige tatsächliche Volatilität getroffen, sondern bestenfalls über die Prognosequalität der ATM-Forward-Volatilität für die zukünftige implizite ATM-Volatilität.

Zudem müssen die Mean-Reversion-Erwartungen auch marktwirksam werden, um der Erwartungstheorie Geltung zu verschaffen. Hierzu werden ggf. erhältliche Forward Start Optionen (mit Laufzeitbeginn und Festlegung des Basispreises nach vereinbarter Moneyness, i.d.R. ATM, erst in der Zukunft), aber i.d.R. deren synthetisches Pendant eingesetzt; letzteres stellt sich als Time Spread dar, also als Verkauf eines Langläufers und Kauf eines Kurzläufers bei einer für überhöht gehaltenen Forward-Volatilität und umgekehrt; durch den ergänzenden Einsatz von Butterfly Spreads kann dies auch cashflow-neutral ausgestaltet werden.

3. Mean Reversion welcher Volatilität? Zumeist wird vernachlässigt, ob sich die Mean-Reversion-Erwartungen auf die tatsächliche oder auf die implizite Volatilität beziehen. Daneben steht sogar noch eine mutmaßliche Mean-Reversion-Erwartung (drift-korrigiert) für das Underlying im Raum, die in realwirtschaftliches oder währungspolitisches Terrain einmündet (vgl. auch Volatility Skew, Ziff. 4.c). Die Frage, auf welche Volatilität sich die Mean-Reversion-Erwartung bezieht, dürfte nur unter Berücksichtigung der unterschiedlichen Populationen der Marktteilnehmer je nach Restlaufzeit beantwortet werden können (vgl. Vega-Trading, Ziff. 2): "Am kurzen Ende" befinden sich Gamma-Trader und (oft unwillkürlich) ins direkte Gamma-Hedging gezungenen Stillhalter und richten ihre Markthandlungen an der tatsächlichen Volatilität aus, während "am langen Ende" die Vega-Trader idealtypisch gar nicht an der tatsächlichen Volatilität interessiert sind, sondern nur daran, wie die anderen Marktteilnehmer deren Entwicklung sehen. Die Person des "intelligenten Market Makers" verknüpft die beiden Bereiche; dennoch ist die Analogie zur Marktsegmentierungstheorie der Zinsstruktur unübersehbar.

Schließlich lässt sich die Frage auch in einer analogen Anwendung der Liquiditätsprämientheorie der Zinsstruktur beleuchten: Die Anbieter von Gamma, genauer: Speed (vgl. Volatility Smile), und Vega, genauer: Vega/Vanna/Volga (vgl. Skew-Risiko, Ziff. 3), könnten für die zu tragenden Volatilitäts- als Hedgerisiken Volatilitätsrisikoprämien i.w.S. verlangen. Dabei deutet das typischerweise zu beobachtende Abflachen von Volatility Smile und Volatility Skew bei längerer Restlaufzeit darauf hin, dass Gamma und Vanna, die in Kurzläufern gehandelt werden, teurer sind als Vega und Volga, die zentraler Marktgegenstand am langen Ende des Marktes sind. Implizite Volatilitäten von Kurzläufern dürften jedenfalls eher die "am Markt" erwartete zukünftige tatsächliche Volatilität und die von Langläufern eher die "am Markt " erwartete zukünftige implizite Volatilität widerspiegeln; im mittleren Laufzeitenbereich könnte eine gemischte Schätzung zu verorten sein.