Kaldors Wachstumsmodell

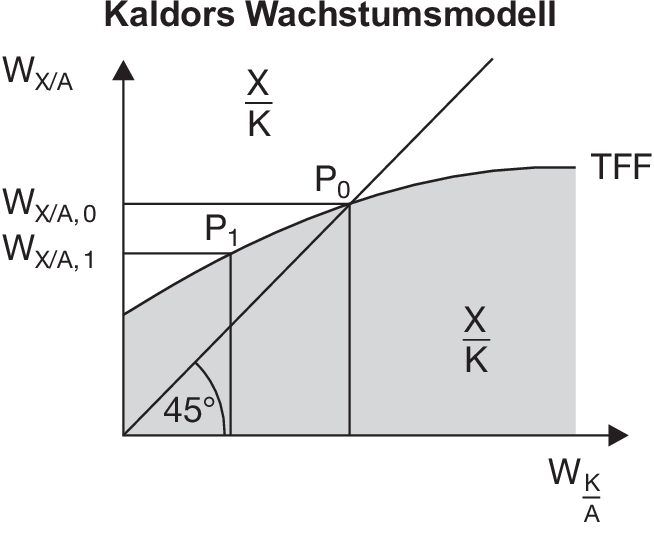
Wachstumsmodell (postkeynesianische Wachstumstheorie) von Kaldor mit den entscheidenden Größen technischer Fortschritt und Profitrate: (1) Technische Fortschrittsfunktion (TFF): Mithilfe der TFF gelingt es Kaldor, den positiven Einfluss eines autonomen und induzierten technischen Fortschritts auf die Höhe der gleichgewichtigen Wachstumsrate der Pro-Kopf-Produktion abzubilden. Die TFF basiert auf einer neoklassischen Produktionsfunktion , die für die Produktionsfaktoren Arbeit, Kapital und technischer Fortschritt sinkende Grenzerträge aufweist. Kaldor endogenisiert und erklärt damit einen Teil des technischen Fortschritts durch die Hypothese, dass mit der Kapitalintensivierung der Produktion weiterer technischer Fortschritt induziert wird. Davon zu unterscheiden ist der autonome technische Fortschritt (F^aut), der unabhängig von der Kapitalintensivierung ist. N. Kaldors TFF beschreibt nun den Einfluss der zunehmenden Kapitalintensivierung T (Erhöhung des Kapitaleinsatzes (K) je Arbeitskraft (A)) und des technischen Fortschritts auf das intensive Wachstum, d.h. auf die Entwicklung des Nationaleinkommens (X) je Arbeitskraft (A):

Der Parameter ist die Summe aus der direkten Produktionselastizität des Kapitals (n) und einem Faktor (a), der angibt, in welchem Ausmaß durch die zunehmende Kapitalintensivierung (positives w_K/A) technischer Fortschritt induziert wird. Diese Gleichung lässt sich auch in der neoklassischen Produktionstheorie ableiten, solange konstant bleibt. Kaldor behauptet jedoch, werde bei rascherer Kapitalintensivierung kleiner. Er begründet dies u.a. damit, dass zunächst die profitabelsten Neuerungen und später die weniger profitablen durchgeführt werden. Ein weiterer Grund liege darin, dass die Lerneffekte, die durch den Umgang mit neuen Maschinen erzielt werden, zunächst stark sind und dann immer mehr abnehmen. Dank des im nächsten Abschnitt erläuterten Stabilisierungsmechanismus wird der Wachstumsprozess immer wieder auf den langfristigen Gleichgewichtspfad zurückgeführt, auf dem Nationaleinkommen und Kapitalbestand mit gleicher Rate wachsen. Die Höhe dieser Rate wird allein von der Lage der TFF bestimmt. Dies zeigt die Gleichsetzung von w_X und w_K in Gleichung (1), die zur Gleichung  (2) führt:

Das Tempo des autonomen und induzierten technischen Fortschritts bestimmt die gleichgewichtige Wachstumsrate der Pro-Kopf-Produktion. Die Durchsetzung des technischen Fortschritts betrachtet Kaldor unter gesellschaftlichem Aspekt und spricht von der technischen Dynamik einer Volkswirtschaft, d.h. von ihrer Bereitschaft, neue Techniken anzuwenden und deren Folgen zu akzeptieren.
(2) Profitratenabhängige Investitionen: Die Unternehmer orientieren sich bei ihrer Investitionsentscheidung an der erwarteten Nachfrageänderung und der erwarteten Änderung der Profitrate bzw. der Verzinsung des eingesetzten Kapitals (G/K); wobei: G = Gewinn = Umsatz - Kosten. Die von Nachfrageänderungen induzierten Investitionen lassen sich aus der TFF ableiten (für w_A = 0):

Festzulegen bleibt, welche Nachfrageänderung (DN) die Unternehmer erwarten. Hier wählt Kaldor die folgenreiche Annahme, die erwartete Nachfrageänderung entspräche stets der Wachstumsrate des Nationaleinkommens der Vorperiode. Dadurch werden destabilisierenden Erwartungsfehler, die im Harrod-Domar-Modell eine entscheidende Rolle spielen, ausgeschlossen. Bei den profitratenabhängigen Investitionen nimmt Kaldor an, dass sich die Unternehmen an der Änderung der Kapitalproduktivität der Vorperiode orientieren. Diese Annahme stützt auf die definitorische Beziehung G/K = X/K · G/X, wonach ein positiver Zusammenhang zwischen der Profitrate G/K und der Kapitalproduktivität X/K besteht, bes. wenn die Gewinnquote (G/X), wie Kaldor annimmt, konstant ist. Daraus folgt für die profitratenabhängigen Investitionen (wobei die Stärke des Einflusses angibt):

Für den gleichgewichtigen Wachstumspfad nimmt Kaldor wie Harrod und Domar Periodengleichgewicht an. Damit gilt auch hier:

Wenn s und konstant sind, befindet sich die mit dieser Rate wachsende Volkswirtschaft im dynamischen Gleichgewicht. Da s annahmegemäß konstant ist, beschränkt sich die Gleichgewichtsbedingung auf die Relation von K und X. Diese darf sich im Zeitablauf nicht verändern, denn nur dann ist konstant. Durch die Annahme N. Kaldors, die nachfrageinduzierten Investitionen orientierten sich an der realisierten Wachstumsrate der Vorperiode, würde in jeder Periode die Wachstumsrate der Vorperiode reproduziert, sofern es nur diese Investitionen gäbe. Da aber zusätzlich zur Nachfrage auch die Profitratenerwartung relevant ist, gibt es nur eine einzige stabile gleichgewichtige Wachstumsrate. Bei dieser ist die Kapitalproduktivität konstant. In der Abbildung „Kaldors Wachstumsmodell” ist sie mit P₀ gekennzeichnet. Solange das reale Inlandsprodukt und der Kapitalbestand mit unterschiedlichen Raten wachsen, ändert sich dagegen mit der Kapitalproduktivität die Profitratenerwartung so, dass die Akkumulationsrate des Kapitals sich der gleichgewichtigen Wachstumsrate annähert. Hinter diesem Stabilisierungsmechanismus steht die Annahme des sinkenden Grenzertrages des Sachkapitals, und zwar trotz des induzierten technischen Fortschritts. Wenn also z.B. in der Abbildung „Kaldors Wachstumsmodell” links von P₀ das Nationaleinkommen rascher wächst als der Kapitalbestand, steigt zwar die Kapitalproduktivität, aber dieser Anstieg ist nicht von Dauer. Vielmehr nähern sich beide Wachstumsraten wegen der zusätzlichen, profitratenabhängigen Investitionen einander an. Im Gleichgewicht ist die Kapitalproduktivität konstant, die Unternehmer rechnen mit einer konstanten Profitrate, und es werden keine profitratenabhängigen Investitionen mehr induziert.

Bild in Originalgröße zeigen

(3) Modifikation: Der Zusammenhang zwischen Profitrate und Kapitalproduktivität ist nicht mehr so eng, wenn die Annahme der konstanten Einkommensverteilung (G/X) fallen gelassen wird, wie die definitorische Beziehung G/K = G/X · X/K zeigt. Es wäre denkbar, dass eine sinkende Gewinnquote die steigende Kapitalproduktivität teilweise oder vollständig kompensiert. Der Stabilisierungsmechanismus ist damit außer Kraft gesetzt. Dass dieser Fall nicht völlig abwegig ist, zeigt die intensivere Auseinandersetzung mit N. Kaldors Verteilungstheorie (Keynes-Kaldor-Verteilungstheorie). Die stabilisierende Wirkung einer variablen Kapitalproduktivität hat Kaldor mit der neoklassischen Wachstumstheorie gemein. Dennoch steuert der Unternehmer durch seine Investitionsentscheidungen den Akkumulationsprozess. In der neoklassischen Wachstumstheorie dagegen passen sich die Unternehmer an Faktorpreisveränderungen an, die mit der variablen Kapitalproduktivität einhergehen.