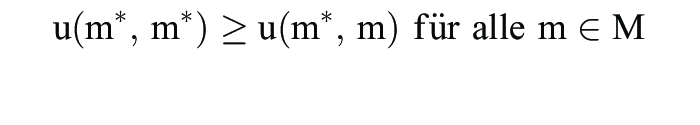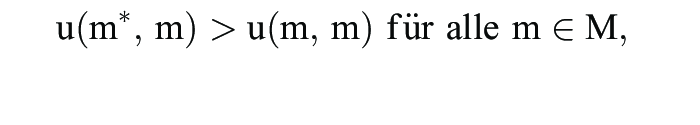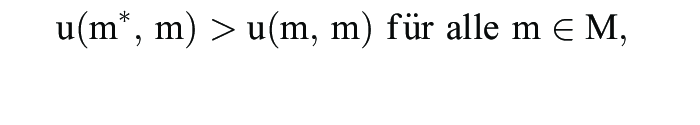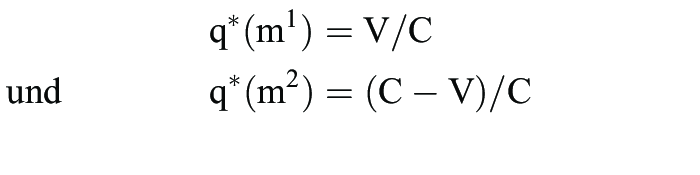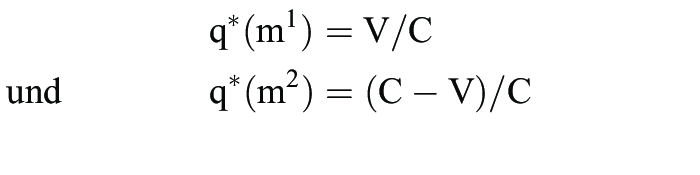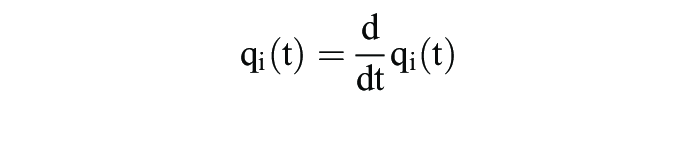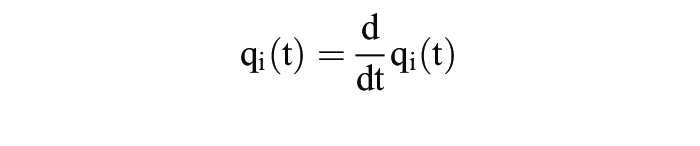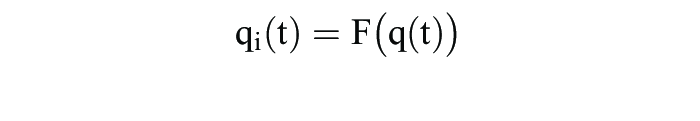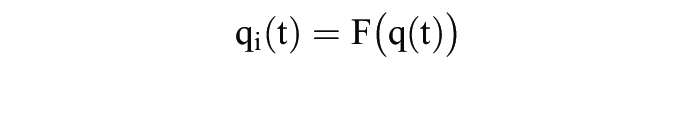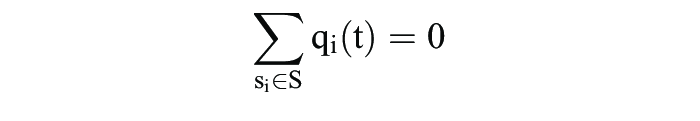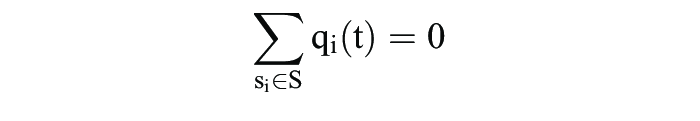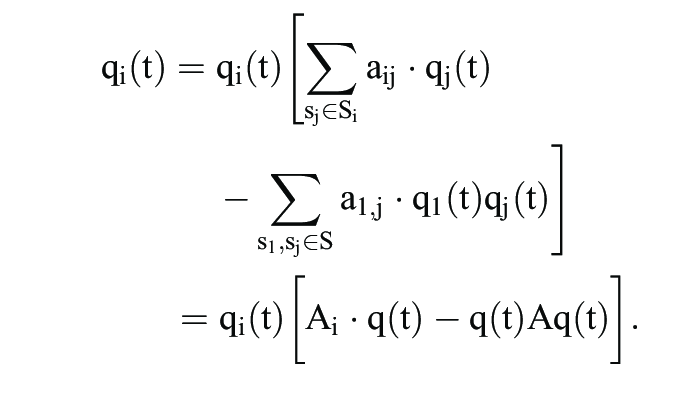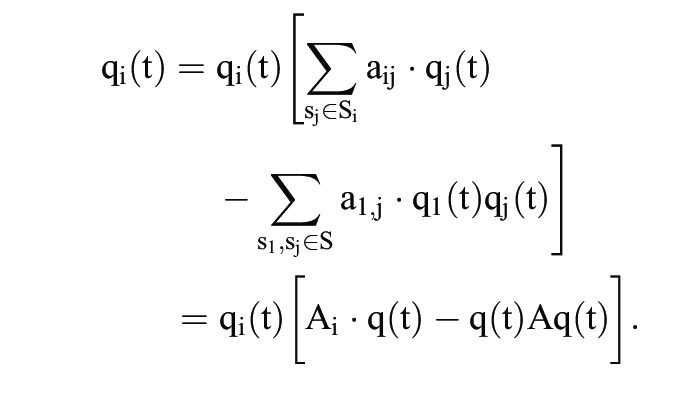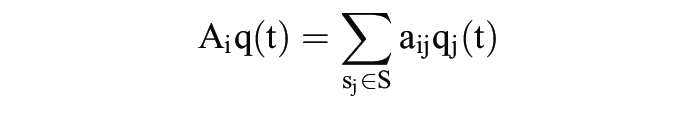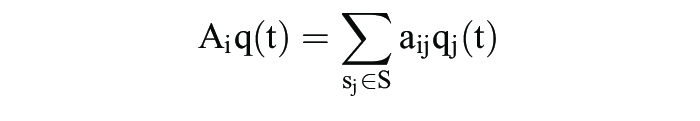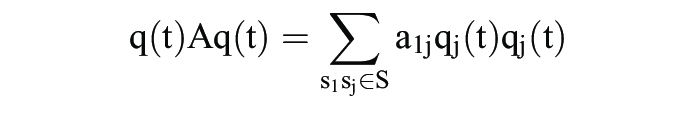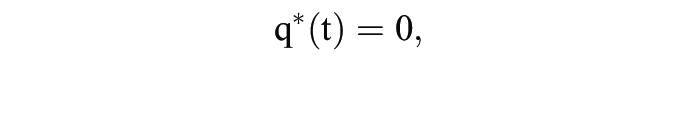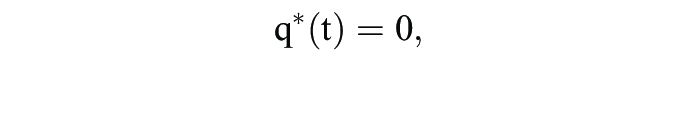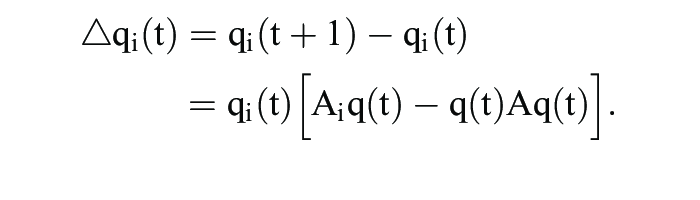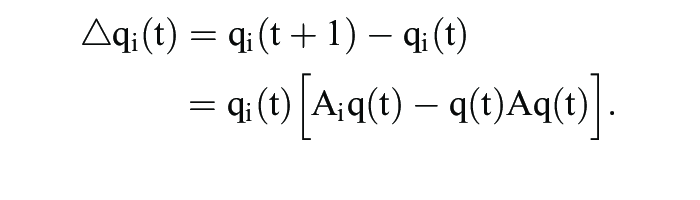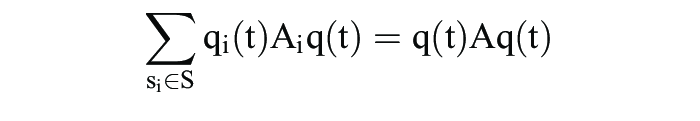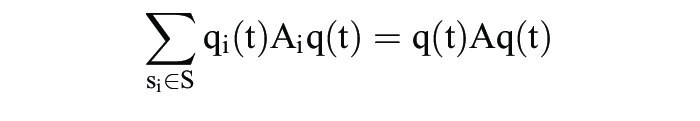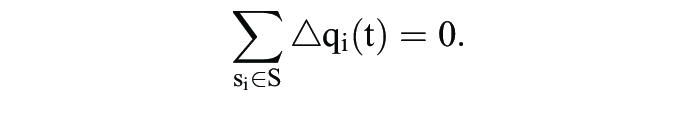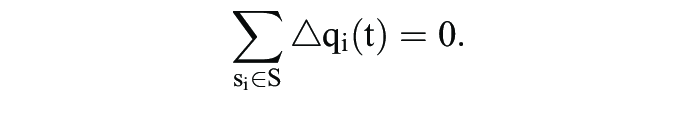Zitierfähige Version
- Revision von evolutionäre Spieltheorie vom 19.02.2018 - 16:04
- Revision von evolutionäre Spieltheorie vom 20.02.2013 - 18:03
- Revision von evolutionäre Spieltheorie vom 16.11.2009 - 15:41
- Revision von evolutionäre Spieltheorie vom 02.10.2009 - 13:13
- Revision von evolutionäre Spieltheorie vom 05.06.2009 - 13:36
evolutionäre Spieltheorie
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
zuletzt besuchte Definitionen...
Von evolutionärer Spieltheorie spricht man meist dann, wenn das Verhalten der Spieler nicht durch rationale Entscheidungskalküle abgeleitet wird, sondern als Ergebnis von kulturellen oder genetischen Evolutionsprozessen begründet wird. Oft kann man die stabilen Ergebnisse solcher Prozesse auch durch statische Stabilitätskonzepte charakterisieren. Ein derartiges Konzept ist die evolutionär stabile Strategie (ESS).
Wie in der Evolutionsbiologie üblich sei von einem symmetrischen 2-Personen-Spiel ausgegangen, das sich durch den für beide Spieler gemeinsamen Strategieraum S1 = S2 = M = {m1, m2, ...} sowie durch die Auszahlungsfunktion bzw. Fitness u(m, ) des Spielers 1 für alle Paare m,
M beschreiben lässt. Eine Strategie m*
M heißt evolutionär stabil, falls die Bedingungen (i)
und (ii)
mit u(m*, m*) = u(m, m*), erfüllt sind. Gemäß der Bedingung (i) erweist sich die Strategiekombination (m*, m*) als symmetrisches Gleichgewicht. Evolutionstheoretisch besagt (i) natürlich, dass nur die am besten angepasste Strategie bzw. Mutante überleben kann (Survial of the Fittest). Durch (ii) wird sichergestellt, dass eine alternative beste Antwort m auf m* sich in einer m*-monomorphen Population nicht ausbreiten kann: Sobald dies der Fall wäre, würde man mit positiver Wahrscheinlichkeit auf m-Gegenspieler treffen, gegen die m* erfolgreicher als m abschneidet. Der Anteil an m-Spielern würde also wieder zurückgedrängt.
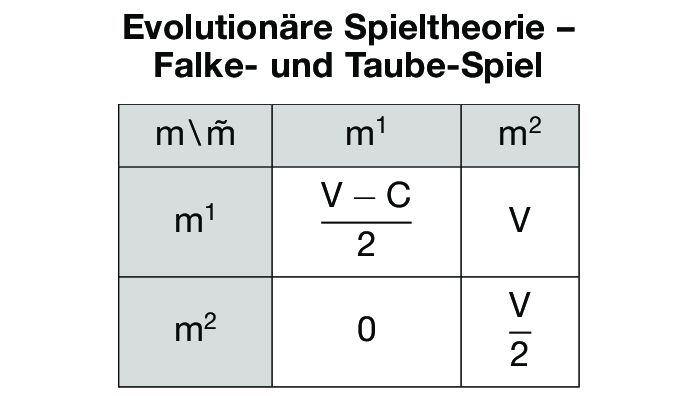
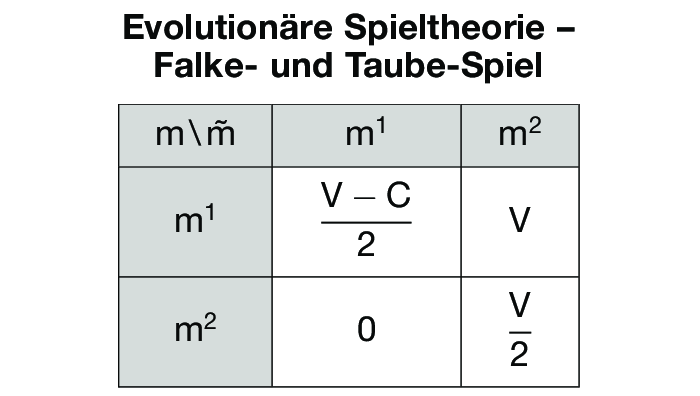
Im Falke- und Taube-Spiel der Abbildung „Evolutionäre Spieltheorie
Falke- und Taube-Spiel” ist nur m* evolutionär stabil, falls V > C > 0, während sich für C > V > 0 nur eine vollständig gemischte Strategie q* mit
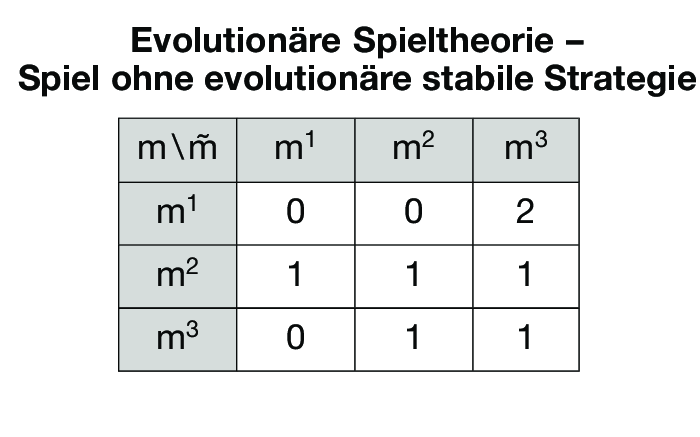
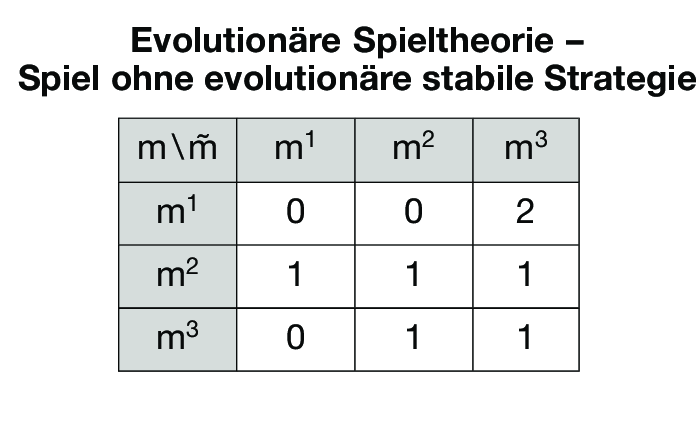
als evolutionär stabil erweist. Im letzteren Fall gilt natürlich u(q, q*) = u(q*, q*) für alle gemischten Strategien q, so dass die Bedingung u(q*, q) > u(q, q) für alle q ≠ q* nachgewiesen werden muss. In der Abbildung „Evolutionäre Speiltheorie - Spiel ohne evolutionäre stabile Strategie” ist keine Strategie m = m1, m2, m3 evolutionär stabil, da m1 und m3 die Bedingung (i) verletzten, während m2 instabil ist, da m3 eine alternative beste Antwort auf m2 darstellt und u(m2, m3) = u(m3, m3) gilt, d.h. m2 ist nur neutral stabil. m2 kann auch als limes evolutionär stabil nachgewiesen werden. Neutral stabile und limes evolutionär stabile Strategien vergröbern das Konzept evolutionär stabiler Strategien, um die Existenz zu gewährleisten. Häufig benutzt man das Konzept evolutionär stabiler Strategien oder analoge Stabilitätsbedingungen für explizit dynamische Beschreibungen der Evolutions- bzw. Lernprozesse. Dynamische Anpassungsprozesse kann man als kontinuierliche oder diskrete Veränderungen modellieren. Bei stetiger Zeit und sehr großer Population lassen sich die Änderungen
der verschiedenen Populationsanteile qi(t) der verschiedenen Strategien si S eines symmetrischen G = (S; A) mit der Auszahltungsmatrix
A = (aij)si,sj S
durch die Differenzialgleichungen der Form
beschreiben, wobei natürlich
gelten muss. Das auch in der Evolutionsbiologie prominenteste Beispiel eines solchen Adaptionsprozesses ist die Replikatordynamik:
Hier bezeichnet Ai die i-te Zeile der Matrix A, d.h.
misst den Erfolg der Strategie si S in einer q(t)-Population. Analog wird durch
der durchschnittliche Erfolg aller Strategien in einer q(t)-Population erfasst. Gemäß der Replikatordynamik erhöt sich damit der Populationsanteil einer Strategie si S dann, wenn sie besser als der Durchschnitt in der durch q(t) beschriebenen Population abschneidet. Offensichtlich ist jeder Gleichgewichtspunkt q* von G = (S; A) ein Ruhepunkt der Replikatordynamik, d.h.
da sich alle Strategien si S mit qi* > 0 als beste Antworten auf q* erweisen. Für diskrete Zeit ergibt sich die Replikatordynamik gemäß
Wegen
gilt die Bedingung
Vgl. auch Spieltheorie.

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon