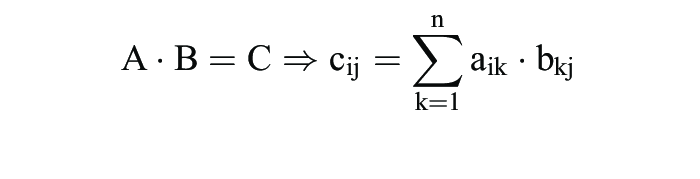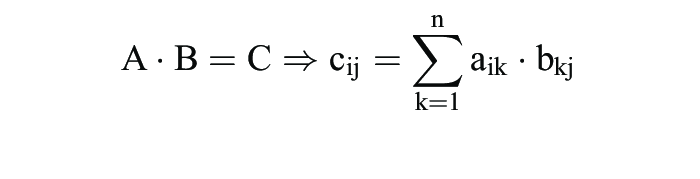Matrizenoperationen

Folgende Matrizenoperationen werden für das Rechnen mit Matrizen (Matrix) benötigt:

(1) Gleichheit von Matrizen:

A = B, wenn alle a_ij = b_ij;

(2) Transponieren (Vertauschen von Zeilen und Spalten):

A A^T a_ij a_ji, für alle i und j;

(3) Addition (nur bei derselben Spalten- und Zeilenzahl):

A + B a_ij + b_ij, für alle i und j;

(4) Multiplikation einer Matrix mit einem Skalar (reelle Zahl):

c · A c · a_ij, für alle i und j;

(5) Skalarprodukt von Vektoren (a' Zeilenvektor, b Spaltenvektor):

a'·b = a₁·b₁ + a₂·b₂ + a₃·b₃ + ... + a_n·b_n ∑ R;

(6) Multiplikation von Matrizen (Spaltenzahl der ersten muss mit der Zeilenzahl der zweiten Matrix übereinstimmen):

Bild in Originalgröße zeigen

oder c_ij: Skalarprodukt der i-ten Zeile von A „mal” der j-ten Spalte von B;

(7) Invertieren: Inverse.