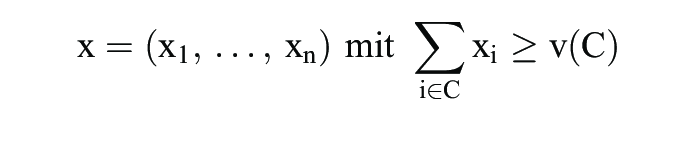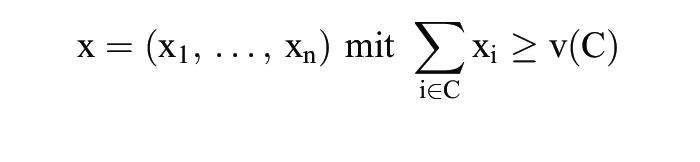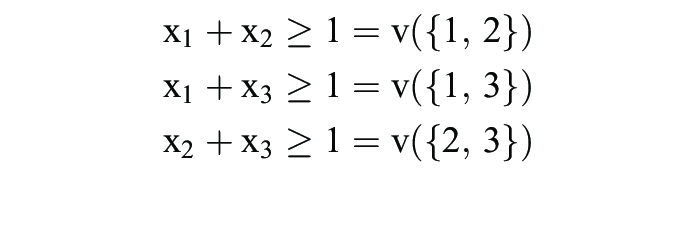kooperative Spieltheorie

häufig von beeindruckender mathematischer Eleganz gekennzeichnet, hat aber in den Wirtschafts- und Sozialwissenschaften wenig Anklang gefunden - Ausnahmen sind die Theorie der Konkurrenzökonomie sowie die experimentelle Wirtschaftsforschung. Ebenso können nichtkooperative Spiele in extensiver Form oder (Agentennormalform) Normalform kooperatives Verhalten abbilden. In der kooperativen Spieltheorie wird dies vorausgesetzt, während es in der nichtkooperativen Theorie durch individuelle Entscheidungen begründet werden muss. Nur die nichtkooperative Theorie kann daher Aussagen über die Bedingungen treffen, die für Kooperation erforderlich sind.

Bezeichnet N die Spielermenge und v(C) den maximalen Gewinn der Mitglieder der Koalition C  N, so ist das wichtige Konzept des Kerns durch die Menge der Auszahlungsvektoren

Bild in Originalgröße zeigen

für C N mit Gleichheit für C = N bestimmt. Gemäß dem mengenwertigen Kern-Konzept verlangt jede Koalition für ihre Mitglieder so viel, wie sie sich selbst sichern kann. Allerdings kann der Kern leer sein, z.B. für N = {1, 2, 3}, v(C) = 1, falls C mindestens zwei Mitglieder enthält, und v(C) = 0 sonst. Da

Bild in Originalgröße zeigen

folgt

2 (x₁ + x₂ + x₃)  3

und damit ein Widerspruch zu

x₁ + x₂ + x₃ = 1.

Andere mengenwertige Lösungskonzepte sind die stabilen Mengen, die Verhandlungsmengen, sowie der Kernel, die zum Teil stets nicht-leer sind. Bes. durch die frühe Anwendung von Edgeworth (1881) hat sich der Kern trotz seiner gelegentlichen Leere als für die Wirtschaftstheorie bedeutsames Lösungskonzept erwiesen. Außer den mengenwertigen Lösungen gibt es die sog. Wertkonzepte der kooperativen Spieltheorie: V.a. die kooperative Verhandlungslösung von Nash (1953), der Wert von Shapley (1953) sowie der von Schmeidler (1969) vorgeschlagene Nucleolus. Die größtenteils axiomatisch begründbaren Konzepte beschreiben Auszahlungsaufteilungen, die gewissen intuitiven Anforderungen entsprechen. Die Wertkonzepte bieten daher Ansatzpunkte, eine willkürfreie Kostenträgerrechnung zu entwickeln.

Vgl. auch Spieltheorie.