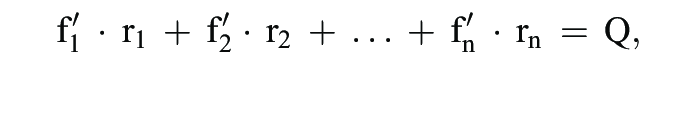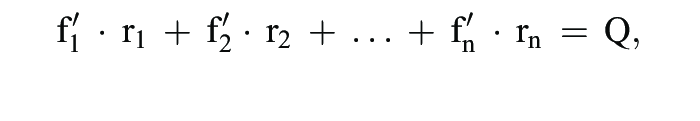Zitierfähige Version
- Revision von Eulersches Theorem vom 19.02.2018 - 15:20
- Revision von Eulersches Theorem vom 28.06.2017 - 14:06
- Revision von Eulersches Theorem vom 03.03.2010 - 13:39
- Revision von Eulersches Theorem vom 17.11.2009 - 16:22
- Revision von Euler'sches Theorem vom 09.10.2009 - 17:00
- Revision von Euler'sches Theorem vom 17.09.2009 - 13:27
- Revision von Euler'sches Theorem vom 05.06.2009 - 13:40
Euler'sches Theorem
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
zuletzt besuchte Definitionen...
Euler-Theorem, Ausschöpfungstheorem, Adding-up-Theorem. Bei linear-homogenen Produktionsfunktionen (vgl. auch Linearhomogenität) gilt:
wobei: f'i = partielle Grenzproduktivität des Faktors i, ri = gesamte Einsatzmenge des Faktors i, Q = Output.
Bei vollständiger Konkurrenz ist das Wertgrenzprodukt p · f'i als Produkt aus Güterpreis p und partieller Grenzproduktivität gleich dem Faktorpreis qi. Multiplikation der obigen Relation mit dem Produktpreis P ergibt daher:
q1 r1 + q2 r2 + ... + qn rn = Q · P.
Die Summe der Kosten für die Produktionsfaktoren zehrt den gesamten Erlös auf, es bleibt kein Gewinn.
Vgl. auch Wicksell-Cobb-Douglas-Produktionsfunktion.

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon