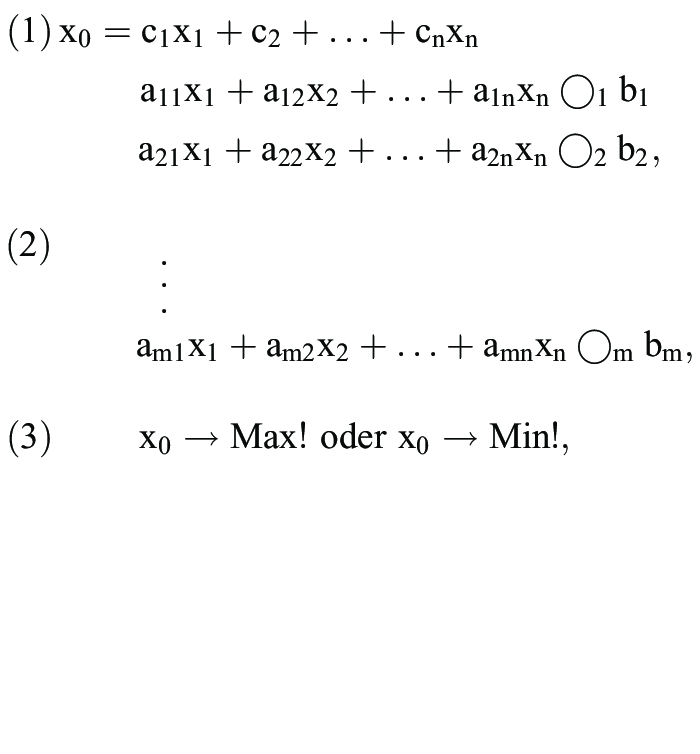Zitierfähige Version
- Revision von lineare Optimierung vom 16.02.2018 - 15:58
- Revision von lineare Optimierung vom 02.02.2018 - 10:13
- Revision von lineare Optimierung vom 20.02.2013 - 17:22
- Revision von lineare Optimierung vom 06.08.2012 - 09:36
- Revision von lineare Optimierung vom 05.05.2010 - 13:24
- Revision von lineare Optimierung vom 24.02.2010 - 14:02
- Revision von lineare Optimierung vom 26.11.2009 - 15:46
- Revision von lineare Optimierung vom 06.10.2009 - 11:39
- Revision von lineare Optimierung vom 17.09.2009 - 13:36
lineare Optimierung
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
zuletzt besuchte Definitionen...
Inhaltsverzeichnis
- Allgemein
- Grundlegende Fragestellungen
- Spezielle Strukturen
- Erweiterungen
- Ökonomische Anwendung
- Neuere Entwicklungen
lineare Planungsrechnung, lineare Programmierung, Linear Programming.
Allgemein
1. Begriff: Teilgebiet des Operations Research (OR), das sich im Wesentlichen mit dem theoretischen Hintergrund von mathematischen Optimierungssystemen der Form
mit zugehörigen Rechenverfahren sowie mit dem Einsatz derartiger Systeme zur Unterstützung ökonomischer Entscheidungsprozesse befasst. In dem System ((1), (2)), das man auch (allg.) lineares Optimierungssystem nennt, steht dabei c1, c2, ... ,cn, a11, a12, ... , amn, b1, b2, ... , bm, für gewisse Konstanten und x1, x2, ..., xn für gewisse reellwertige Variablen, die stets so zu wählen sind, dass sämtliche Restriktionen von (2) erfüllt sind, d.h., das Restriktionssystem (2) beschreibt eine gewisse Lösungsmenge.
Jeder Lösung aus dieser Lösungsmenge ist durch die Funktion (1) (Zielfunktion) eine Zahl x0 (Zielwert) zugeordnet, die in Verbindung mit einer der Vorschriften von (3) (Zielvorschrift) eine Beurteilung der Güte der betreffenden Lösung erlaubt. Die Zielvorschrift x0 → Max! besagt dabei, dass eine Lösung mit einem größeren Zielwert besser ist als jede andere Lösung mit einem kleineren (größeren) Zielwert.
Die Charakterisierung von Systemen des Typs ((1), (2)) als linear erklärt sich insofern, dass die Zielfunktion (1) und sämtliche Restriktionen (2) linear sind (lineare Zielfunktion, lineare Restriktion).
Grundlegende Fragestellungen
1. Optimale Lösung: Im Zusammenhang mit linearen Optimierungssystemen drängt sich die Frage auf, welche Lösung von (2) den durch (1) definierten Zielwert x0 maximiert (oder minimiert) bzw. wie man ggf. erkennt, dass eine solche optimale Lösung nicht existiert. Zur Beantwortung derartiger Fragen wurden eine ganze Reihe von Verfahren (Simplexmethoden) entwickelt und in entsprechende Standardsoftware eingebettet, die geeignet ist, auch sehr große Probleme der Praxis (d.h. Probleme mit vielen Variablen und Restriktionen) zu lösen.
2. Beim Einsatz linearer Optimierungssysteme in der Praxis besteht häufig Ungewissheit über die tatsächlichen numerischen Werte der Koeffizienten c1, ..., cn, a11, ..., amn, b1, ..., bm; z.T. ist sogar unklar, ob bestimmte Restriktionen von (2) überhaupt auftreten. Wie man im Hinblick auf derartige Situationen - ausgehend von einer ersten optimalen Lösung - auf einem möglichst einfachen Wege Alternativrechnungen (postoptimale Rechnungen) durchführen kann, ist eine weitere Problemstellung.
3. Vor dem gleichen Hintergrund untersucht man im Rahmen von Sensitivitätsanalysen, wie sich bestimmte Koeffizienten (v.a. die Koeffizienten c1, ..., cn der Zielfunktion (1) bzw. die rechten Seiten b1, ..., bm der Restriktionen (2)) ändern dürfen, ohne dass eine gefundene optimale Lösung (bzw. eine gefundene kanonische Form des Optimierungssystems) die Eigenschaft der Optimalität verliert.
4. Die parametrische lineare Optimierung befasst sich mit der noch erweiterten Fragestellung, welche optimalen Lösungen sich jeweils ergeben, wenn gewisse Koeffizienten (Koeffizienten der Zielfunktion und/oder die rechten Seiten der Restriktionen) in Abhängigkeit von einem oder mehreren Parametern schwanken können.
5. Die Dualitätstheorie der linearen Optimierung untersucht den Zusammenhang zwischen gewissen Paaren von linearen Optimierungssystemen. Ihre Erkenntnisse sind für die Entwicklung von Rechenverfahren von Bedeutung.
6. Die bei Anwendung in der Praxis vorkommenden linearen Optimierungssysteme sind i.d.R. sehr groß (viele Variablen, viele Restriktionen), so dass die Bestimmung einer optimalen Lösung mit herkömmlichen Lösungsverfahren sehr viel Rechenzeit und Speicherplatz beanspruchen kann. Es lässt sich jedoch oft beobachten, dass die jeweiligen Koeffizientenmatrizen nur wenige von Null verschiedene Koeffizienten a11, ..., amn (dünn besetzte Matrix) aufweisen. Fragen im Zusammenhang mit deren Ausnutzung stellen sich im Hinblick auf die Entwicklung schnellerer, weniger speicherplatzintensiver Lösungsverfahren.
Spezielle Strukturen
Optimierungssysteme der Praxis zeichnen sich i.d.R. nicht nur durch dünn besetzte Koeffizientenmatrizen aus, die von Null verschiedenen Koeffizienten sind außerdem oft nach einem gewissen Schema angeordnet. Derartige speziell strukturierte Systeme ergeben sich etwa bei der mathematischen Formulierung von Transportproblemen und Zuordnungsproblemen, von Wege- und Flussproblemen in Graphen (Netzplantechnik). Sie lassen sich mit traditionellen Simplexmethoden lösen, daneben gibt es aber Lösungsverfahren, die durch eine Ausnutzung der jeweiligen speziellen Koeffizientenstruktur erhebliche Vorteile in Bezug auf Rechenzeit und Speicherbedarf erzielen.
Erweiterungen
Durch bestimmte Umformungen und Techniken lassen sich die Methoden der linearen Optimierung z.T. auch zur Untersuchung von Fragen über solche Optimierungssysteme einsetzen, deren Struktur nur unvollständig mit der des Systems ((1), (2)) übereinstimmt: 1. Gewisse (d.h. mind. eine, möglicherweise aber auch alle) Variablen dürfen nur ganze Zahlen (ganzzahliges Optimierungsproblem) bzw. nur die Werte Null oder Eins annehmen (binäres Optimierungsproblem).
2. Gewisse Probleme der nicht-linearen Optimierung lassen sich ebenfalls mit linearen bzw. geringfügig modifizierten linearen Methoden lösen. Hierzu gehört u.a. die Bestimmung von optimalen Lösungen für quadratische Optimierungsprobleme und bestimmte separable Optimierungsprobleme.
3. Im Rahmen der linearen Optimierung bei mehrfacher Zielsetzung stehen solche linearen Optimierungssysteme im Mittelpunkt, bei denen den Lösungen des Restriktionssystems (2) anhand verschiedener Zielfunktionen gleichzeitig mehrere Zielwerte zugeordnet sind. Nur in ganz seltenen Ausnahmefällen existiert jetzt noch eine Lösung, die im Hinblick auf alle Zielfunktionen und -vorschriften gleichzeitig optimal ist. Die für diese Optimierungssysteme entwickelten Verfahren bezwecken deshalb nicht die Ableitung einer in diesem Sinn idealen Lösung, sondern es geht vielmehr um die Ableitung von allen oder einigen effizienten Lösungen bzw. bei interaktiven Verfahren um die Ermittlung einer für den Entscheidungsträger akzeptablen Kompromisslösung.
Ökonomische Anwendung
Von allen Methoden des Operations Research haben diejenigen der linearen Optimierung (neben denen der Netzplantechnik) die weiteste Verbreitung in der ökonomischen Praxis gefunden und sich bewährt. Empirischen Untersuchungen zufolge liegen ihre Einsatzschwerpunkte in der Grundstoff-, der Chemischen, der Eisen- und Stahl- sowie der Nahrungs- und Genussmittelindustrie. Bez. der betrieblichen Funktionsbereiche sind in erster Linie Anwendungen im Produktionsbereich (zur Lösung von Problemen der Produktionsprogrammplanung, Produktionssteuerung und Zuschnittplanung), im Absatzbereich (Transportproblem), in der Lagerhaltung (Bestimmung optimaler Lagerbestände) sowie im Beschaffungsbereich (Transportproblem, Mischungsproblem, Bestellmengenproblem) anzuführen.
In stärkerem Maße setzen sich schließlich auch integrierte Modelle zur simultanen Planung verschiedener Funktionsbereiche (Produktions- und Absatzbereichs) durch.
Neuere Entwicklungen
Theoretische, am Worst-Case-Verhalten von Algorithmen orientierte Überlegungen haben Zweifel an der rechentechnischen Vorteilhaftigkeit der (in der Praxis gewährten) Simplexmethoden entstehen lassen. Dieser Umstand führte zur Entwicklung des zwar theoretisch günstigeren Ellipsoid-Verfahrens, das sich bei konkreten Vergleichsrechnungen aber (mit Ausnahmen einiger künstlich konstruierter Sonderfälle) als praktisch schlechter erwies.

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon