Erwartungswert-Varianz-Prinzip

1. Darstellung: Entscheidungsprinzip bei Risiko, kurz (μ,σ)-Prinzip genannt. Bei Anwendung des (μ,σ)-Prinzips ist die Präferenzfunktion über den Erwartungswert μ und die Varianz (σ²) bzw. Standardabweichung σ des Ergebnisses definiert. Die Präferenzfunktion ist entsprechend zu konkretisieren, d.h. der Entscheider muss spezifizieren, wie μ und σ in die Präferenzfunktion eingehen.

Für den Erwartungswert, die Varianz und die Standardabweichung des unsicheren Ergebnisses x_a einer Alternative A_a gilt:

Der Präferenzwert einer Alternative ist durch

gegeben, und die Entscheidungsregel lautet

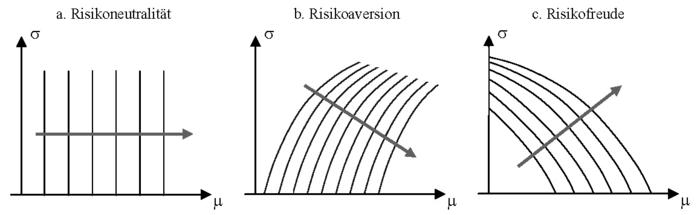
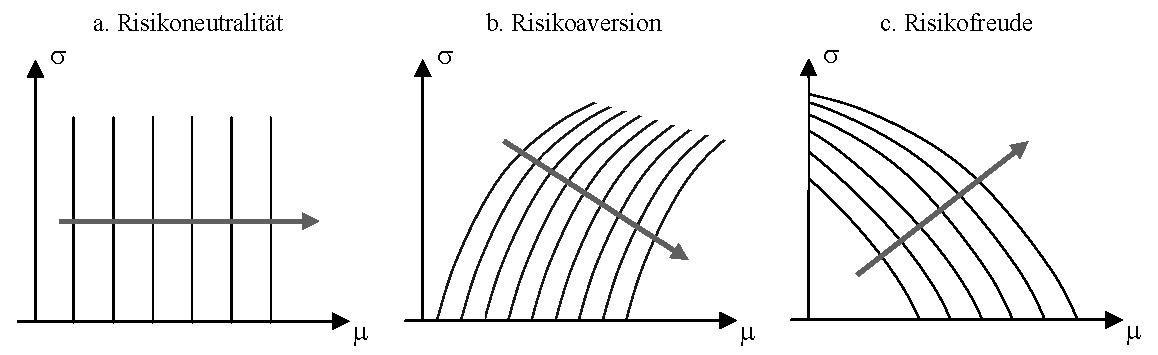
2. Anwendung: Das (μ,σ)-Prinzip erlaubt es einem Entscheider auf einfache Weise, das Risiko einer Alternative bei der Bewertung zu berücksichtigen. Ist der Entscheider risikoavers, so geht σ negativ in die Präferenzfunktion ein, ist er risikofreudig, so geht σ positiv in Φ(μ,σ) ein. Nur risikoneutrale Entscheider berücksichtigen σ gar nicht, sondern allein μ. Aufgrund der Abhängigkeit des Präferenzwertes von nur zwei Parametern lassen sich die Präferenzen eines (μ,σ)-Entscheiders anschaulich in Form eines Indifferenzkurvensystems darstellen, vgl. nachstehende Abb.

Bild in Originalgröße zeigen

Eine Indifferenzkurve ist der geometrische Ort aller Kombinationen aus μ und σ, die der Entscheider als gleichwertig einschätzt, für die also der Präferenzwert Φ(μ,σ) identisch ist. In den Abb. kennzeichnen die Pfeile die Richtung, in denen Indifferenkurven höhere Präferenzniveaus repräsentieren. In Abb. a verlaufen die Indifferenzkurven parallel zur μ-Achse. D.h., dass Veränderungen von σ nicht zu Änderungen des Präferenzwertes führen; der Entscheider ist risikoneutral. In Abb. b steigen die Indifferenzkurven. D.h., dass eine Erhöhung von σ nur dann zum gleichen Präferenzwert führt, wenn auch μ erhöht wird; der Entscheider ist risikoavers. In Abb. c dagegen sinken die Indifferenzkurven. D.h., dass eine Senkung von σ nur dann zum gleichen Präferenzwert führt, wenn μ erhöht wird; der Entscheider muss für die Senkung des Risikos kompensiert werden, ist also risikofreudig.

3. Beurteilung: Das (μ,σ)-Prinzip ist aufgrund seiner Flexibilität in der Abbildung von Risikopräferenzen ein einfaches und dennoch breit anwendbares Entscheidungsprinzip bei Risiko. Es liegt der Portefeuille-Theorie und damit dem Capital Asset Pricing Model zugrunde (Kapitalmarkttheorie). Gleichwohl ist es nur in Spezialfällen vereinbar mit dem Bernoulli-Prinzip (der Erwartungsnutzentheorie). Hauptproblem des (μ,σ)-Prinzips ist, dass gegen Dominanzkriterien (absolute Dominanz, Zustandsdominanz, stochastische Dominanz) verstößt.