Substitutionselastizität

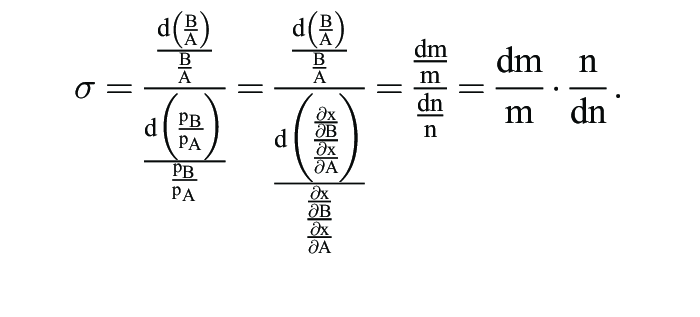
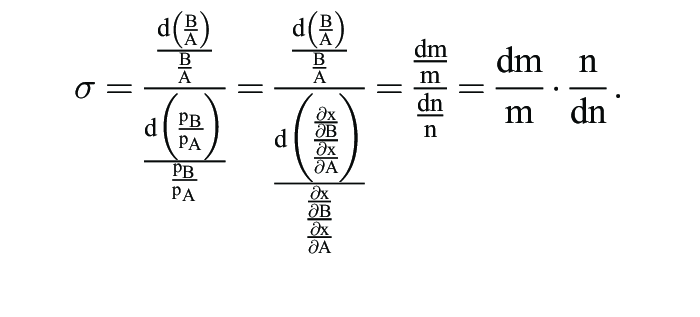
Quotient aus der relativen Veränderung des Faktoreinsatzverhältnisses m und der relativen Veränderung des Faktorpreisverhältnisses n. Wird vorausgesetzt, dass die Minimalkostenkombination in Bezug auf die Produktionsfaktoren A und B erfüllt ist, gilt:

sodass n auch für das Verhältnis der Grenzerträge bzw. für die Grenzrate der Substitution stehen kann. Dies ermöglicht es, die Substitutionselastizität als nur von der Produktionsfunktion abhängige Größe zu bestimmen. Es gilt also:

Bild in Originalgröße zeigen

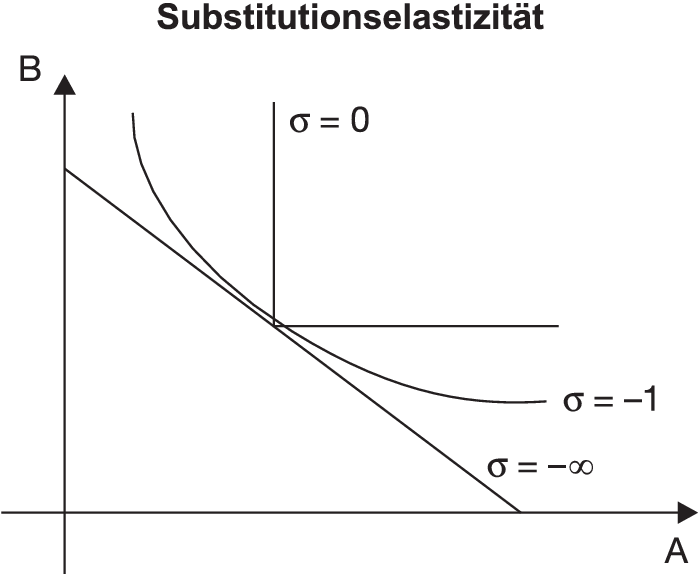
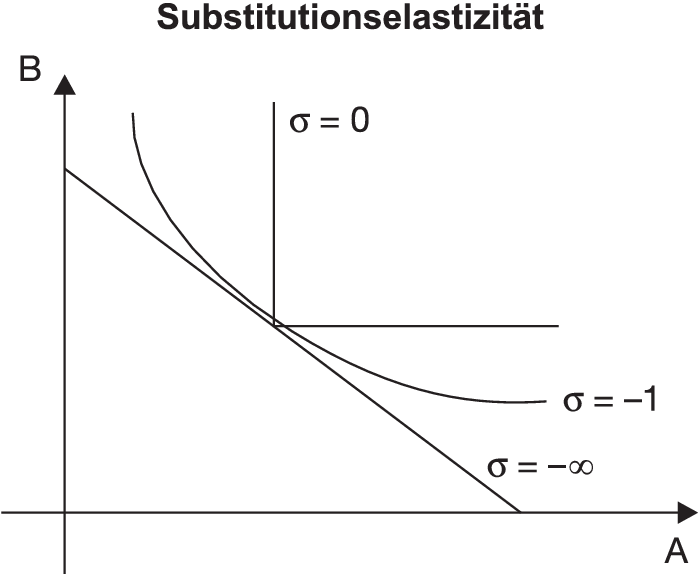
Die Substitutionselastizität nimmt in Abhängigkeit von der Produktionsfunktion unterschiedliche Werte an. Solche Produktionsfunktionen, für die die Substitutionselastizität konstant ist, werden als CES-Funktionen bezeichnet. Wichtige CES-Funktionen stellen die Wicksell-Cobb-Douglas-Produktionsfunktion (σ = -1), die Leontief-Produktionsfunktion (limitationale Produktionsfaktoren, σ = 0) und die lineare Produktionsfunktion mit vollkommenen substituierbaren Produktionsfaktoren (σ = − ∞) dar. Diese Fälle lassen sich durch die Form der Isoquanten charakterisieren (vgl. Abbildung „Substitutionselastizität”).

Bild in Originalgröße zeigen

Die Substitutionselastizität steht in enger Beziehung zur Verteilung des Erlöses bzw. (auf volkswirtschaftlicher Ebene) des Einkommens auf die Faktoren. Aus dem Verhältnis der Erlösanteile E_A = A · p_A und E_B = B · p_B der Faktoren A und B, nämlich

folgt:

mithin

Ist σ = 0, folgt:

d.h., die Verteilung für den sich z.B. relativ verteuernden Faktor B verbessert sich. Für σ = –1 bleibt die Verteilung

(wegen dv/dn = 0) unverändert, Steigerung des Faktorpreisverhältnisses und Abnahme des Faktoreinsatzverhältnisses (oder umgekehrt) kompensieren sich hier exakt in ihrer Wirkung. Im Fall σ = – wird etwa der Faktor B bei relativer Verteuerung völlig aus dem Produktionsprozess verdrängt.