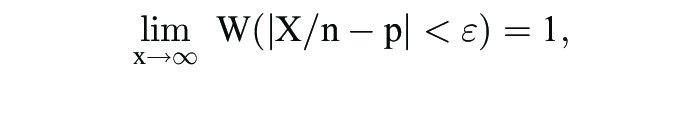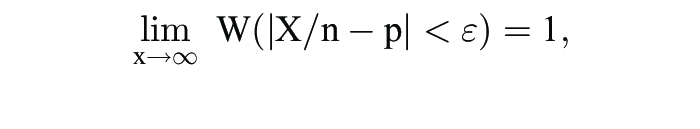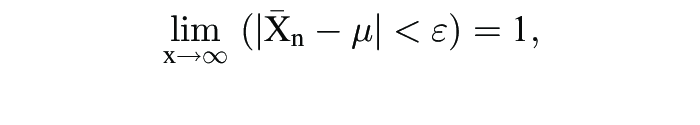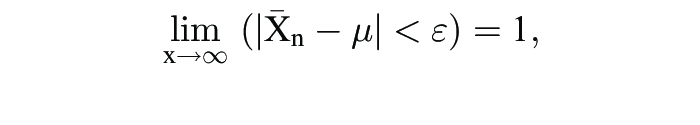Gesetze der großen Zahlen

zusammenfassende Bezeichnung für mehrere Konvergenzaussagen über Folgen von Zufallsvariablen mit großer Bedeutung für die Anwendung in der Stichprobenpraxis.

1. Das Bernoullische Gesetz der großen Zahlen betrifft einen Zufallsvorgang, bei dem mit Wahrscheinlichkeit p ein Erfolg resultiert. Bei n-maliger unabhängiger Wiederholung dieses Vorgangs ist die Anzahl X_ν der zu erzielenden Erfolge binomialverteilt (Binomialverteilung) mit Parametern n und p. Es gilt

Bild in Originalgröße zeigen

d.h. für zunehmendes n konvergiert die relative Häufigkeit stochastisch gegen p.

2. Das Chintschinsche Gesetz der großen Zahlen betrifft eine Folge {X_ν} stochastisch unabhängiger (stochastische Unabhängigkeit) Zufallsvariablen mit identischer, aber beliebiger Verteilung und endlichem Erwartungswert E(X_ν) = µ. Es gilt

Bild in Originalgröße zeigen

d.h. der Stichprobendurchschnitt _ν konvergiert für zunehmendes n gegen den Erwartungswert µ.