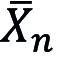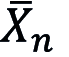Gesetze der großen Zahlen

zusammenfassende Bezeichnung für Konvergenzaussagen über Folgen von Zufallsvariablen mit großer Bedeutung für die Anwendung in der Statistik. Schwaches und Starkes Gesetz großer Zahlen machen Aussagen über die Konvergenz von arithmetischen Mitteln gegen einen Erwartungswert.

1. Beim Schwachen Gesetz großer Zahlen wird eine Folge stochastisch unabhängiger (stochastische Unabhängigkeit) Zufallsvariablen X₁, X₂, ... betrachtet, für die EX_i = μ (Erwartungswert) und Var X_i ≤ M < ∞ (Varianz) für eine positive Konstante M und für alle natürlichen Zahlen i gelte. Dann konvergiert die Folge der arithmetischen Mittel 

Bild in Originalgröße zeigen

stochastisch gegen den Erwartungswert μ; genauer:

für jedes ε > 0.

2. Sind in 1. die Zufallsvariablen speziell Bernoulli-verteilt, d.h. P(X_i=1) = p und P(X_i=0) = 1-p für ein p mit 0<p<1 und für alle natürlichen Zahlen i, dann ist die Zufallsvariable S_n= X₁+...+X_n  binomialverteilt (Binomialverteilung) mit den Parametern n und p, und es gilt

für jedes ε > 0. Die Aussage wird auch als das Bernoullische Gesetz der großen Zahlen bezeichnet. Als eine zentrale Grundlage der Statistik besagt dieses Gesetz, dass die relativen Häufigkeiten S_n/n gegen den Erwartungswert p beziehungsweise gegen die "wahre Trefferwahrscheinlichkeit" p konvergieren. In diesem Sinne ist das arithmetische Mittel S_n/n also in der schließenden Statistik eine geeignete Schätzfunktion für den unbekannten Parameter p; diese Eigenschaft wird als schwache Konsistenz des Schätzers  S_n/n bezeichnet.  

3. Eine Version des Starken Gesetzes großer Zahlen besagt, dass die Folge der arithmetischen Mittel aus 1. für stochastisch unabhängige und identisch verteilte Zufallsvariablen X₁, X₂, ... auch fast sicher gegen den Erwartngswert μ konvergiert.