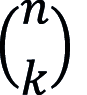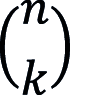Binomialverteilung
GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
Übersicht
zuletzt besuchte Definitionen...
spezielle diskrete Wahrscheinlichkeitsverteilung mit der Wahrscheinlichkeitsfunktion (Zähldichtefunktion)
Dabei ist
ein Binomialkoeffizient.
Wenn die Zufallsvariable X eine Binomialverteilung mit den Parametern n (natürliche Zahl) und p mit 0 < p < 1 besitzt, dann gilt:
P(X = k) = b(k|n;p) , k = 0, 1, ..., n.
Der zugehörige Erwartungswert ist np und die Varianz np(1-p). Die Binomialverteilung mit Parametern n und p erfasst folgenden Sachverhalt: In einer Grundgesamtheit befinden sich zwei Sorten von Elementen mit den Anteilswerten p bzw. 1–p. Es werden nach dem einfachen Urnenmodell mit Zurücklegen n Elemente entnommen. Dann gibt b(k|n;p) die Wahrscheinlichkeit dafür an, dass genau k Elemente der ersten Sorte in die Ziehung gelangen. Für große n kann die Binomialverteilung u.a. durch die Normalverteilung approximiert werden (Approximation).
Beispiel: Stichprobe vom Umfang n aus einer Produktion mit dem Anteil p defekter Teile; b(k|n;p) ist dann die Wahrscheinlichkeit für genau k defekte Teile in der Stichprobe.
