Normalverteilung
Übersicht
zuletzt besuchte Definitionen...
Gaußsche Normalverteilung; eine in der Inferenzstatistik bes. wichtige Wahrscheinlichkeitsverteilung benannt nach C.F. Gauß. Die Dichtefunktion einer Normalverteilung mit den Parametern μ und σ2>0 hat die Form
für -∞ < x < ∞ .
1. Die Parameter der Normalverteilung sind der Erwartungswert μ und die Varianz σ2. Mithilfe der Standardtransformation können Normalverteilungen mit beliebiger Parameterlage in die Standardnormalverteilung (μ = 0; σ2 = 1) überführt werden. Hat die Zufallsvariable X eine Normalverteilung mit den Parametern μ und σ2, so hat die Zufallsvariable (X-μ)/σ eine Standardnormalverteilung. Für die Auswertung der Dichtefunktion bzw. Verteilungsfunktion der Standardnormalverteilung existieren Tabellenwerke, in denen Werte der Verteilungsfunktion verzeichnet sind. Die Tabellen der Standard-Normalverteilung können daher zur Auswertung beliebiger Normalverteilungen herangezogen werden.
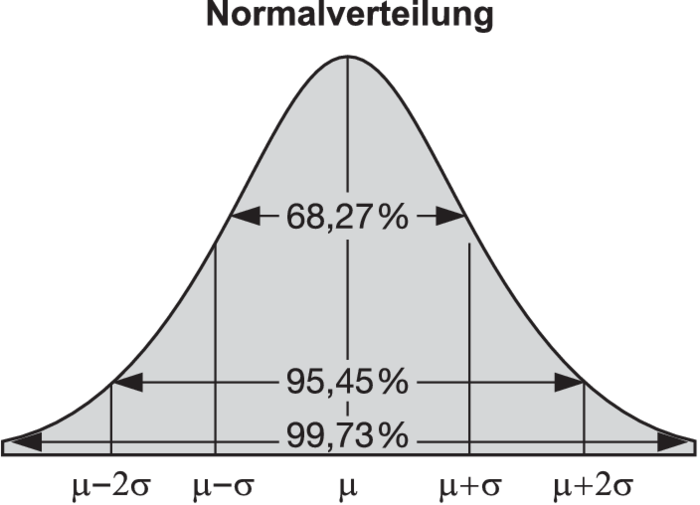
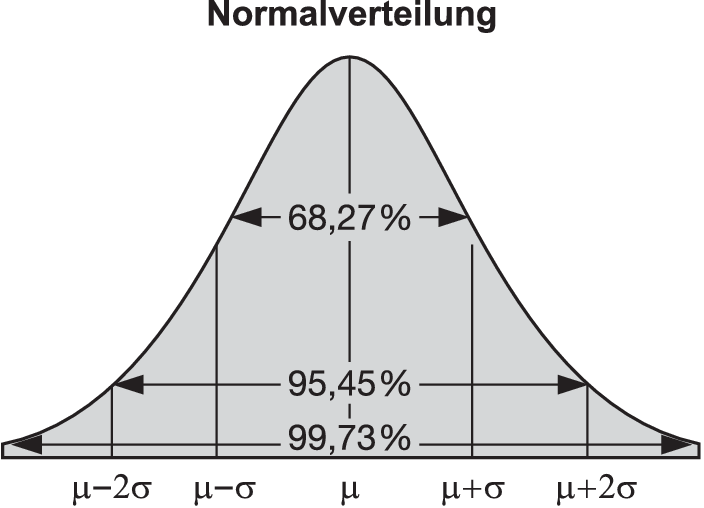
2. Eigenschaften: Bei grafischer Darstellung ergibt die Dichtefunktion einer Normalverteilung eine glockenförmige Kurve, die symmetrisch zur Geraden x = μ ist. Der Erwartungswert μ fällt mit dem Modus und dem Median zusammen. Die Glockenkurve hat Wendepunkte bei den Abszissen μ + σ bzw. μ - σ. Für eine μ-normalverteilte Zufallsvariable X gilt (gerundete Werte): P(μ - σ ≤ X ≤ μ + σ) = 0,6827; P(μ - 2σ ≤ X ≤ μ + 2σ) = 0,9545; P(μ - 3σ ≤ X ≤ μ + 3σ) = 0,9973.
Vgl. Abbildung „Normalverteilung“.
3. Bedeutung: Annähernd normalverteilte Merkmale sind in der Wirtschaft und im technisch-naturwissenschaftlichen Bereich gelegentlich zu beobachten. So ist z.B. der Stichprobendurchschnitt (arithmetisches Mittel) bei großem Stichprobenumfang unter geeigneten Voraussetzungen annähernd auch dann als normalverteilt zu betrachten, wenn über die Verteilung der Grundgesamtheit nichts bekannt ist. Dies ist durch den Zentralen Grenzwertsatz begründbar. Die Normalverteilung wird unter gewissen Voraussetzungen zur Approximation vieler theoretischer Verteilungen verwendet, etwa der Binomialverteilung, der hypergeometrischen Verteilung, der Poissonverteilung oder der Chi-Quadrat-Verteilung.
Literaturhinweise SpringerProfessional.de
Bücher auf springer.com
Interne Verweise
Normalverteilung
- Approximation
- Binomialverteilung
- Chi-Quadrat-Test
- Chi-Quadrat-Verteilung
- Eulersche Zahl
- Galtonsches Brett
- Gaußsche Normalverteilung
- Grenzwertsatz
- hypergeometrische Verteilung
- Korrelationskoeffizient
- Lageparameter
- nicht-parametrische (verteilungsfreie) Testverfahren
- Robustheit
- Standardnormalverteilung
- Standardtransformation
- statistische Testverfahren
- Stetigkeitskorrektur
- Stichprobenverteilungen
- Varianzanalyse
- Wahrscheinlichkeitsnetz
- Zufallszahlen
Normalverteilung
- arithmetisches Mittel
- Binomialverteilung
- Chi-Quadrat-Verteilung
- Dichtefunktion
- Erwartungswert
- Grenzwertsatz
- Grundgesamtheit
- hypergeometrische Verteilung
- Inferenzstatistik
- Median
- Modus
- Parameter
- Poissonverteilung
- Standardnormalverteilung
- Standardtransformation
- Varianz
- Verteilungsfunktion
- Verteilungsfunktion