Zitierfähige Version
- Revision von Gini-Koeffizient vom 19.02.2018 - 15:54
- Revision von Gini-Koeffizient vom 27.09.2017 - 14:53
- Revision von Gini-Koeffizient vom 18.08.2017 - 15:08
- Revision von Gini-Koeffizient vom 05.07.2013 - 15:48
- Revision von Gini-Koeffizient vom 20.03.2013 - 10:15
- Revision von Gini-Koeffizient vom 25.02.2013 - 13:08
- Revision von Gini-Koeffizient vom 13.01.2010 - 14:07
- Revision von Gini-Koeffizient vom 17.11.2009 - 14:25
- Revision von Gini-Koeffizient vom 03.09.2009 - 15:40
- Revision von Gini-Koeffizient vom 22.06.2009 - 13:46
- Revision von Gini-Koeffizient vom 05.06.2009 - 15:05
Gini-Koeffizient
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
zuletzt besuchte Definitionen...
Inhaltsverzeichnis
Gini-Index.
Statistik
Maßgröße zur Kennzeichnung der relativen Konzentration. Ist das arithmetische Mittel der Werte x1, ..., xn ≥ 0 , so ist der Gini-Koeffizient durch
definiert. Der Gini-Koeffizient ist als relatives Streuungsmaß zu interpretieren. Er kann auch mithilfe der Lorenzkurve bestimmt werden. Für den Gini-Koeffizienten gilt stets
Die Kenngröße G* mit
mit 0 ≤ G* ≤ 1 wird als normierter Gini-Koeffizient bezeichnet.
Verteilungstheorie und -politik
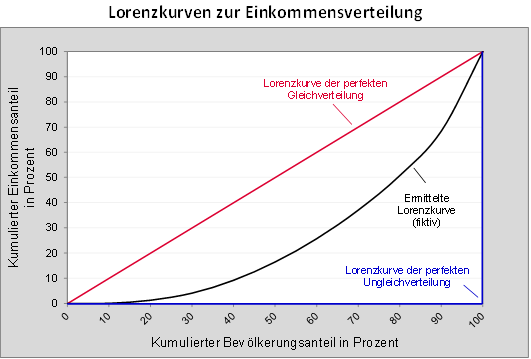
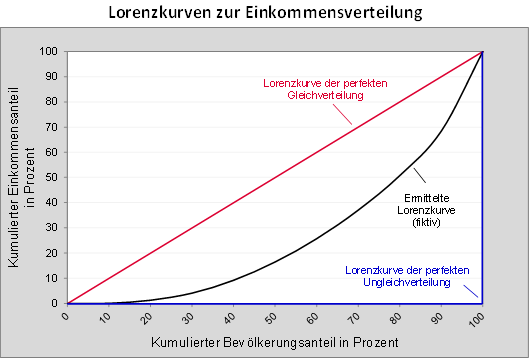
Der Gini-Koeffizient ist ein weit verbreitetes Maß zur Quantifizierung der relativen Konzentration einer Einkommensverteilung. Im Falle der maximalen Gleichverteilung der Einkommen (d.h. jede Person bezieht exakt das Durchschnittseinkommen der betrachteten Grundgesamtheit) nimmt der Gini-Koeffizient den Wert Null an, während er im anderen Extremfall einer maximal ungleichen Einkommensverteilung (d.h. eine einzige Person bezieht das komplette Einkommen der betrachteten Grundgesamtheit für sich alleine) den Wert Eins annimmt. Der Gini-Koeffizient lässt sich mithilfe der Lorenzkurve veranschaulichen und bestimmen (vgl. Abbildung „Lorenzkurven zur Einkommensverteilung“). Der Gini-Koeffizient entspricht dabei der Fläche zwischen der Winkelhalbierenden (Gerade der perfekten Gleichverteilung) und der entsprechend ermittelten Lorenzkurve in Relation zur Gesamtfläche unterhalb der Winkelhalbierenden (Dreiecksfläche zwischen der Winkelhalbierenden und der Geraden der perfekten Ungleichverteilung).

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon