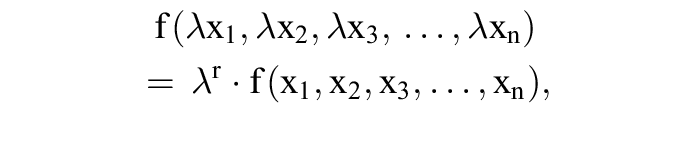Homogenität

1. Begriff: Eine Funktion f: Rⁿ → R heißt homogen vom Grad r, wenn für jede reelle Zahl λ > 0 die Beziehung gilt:

Bild in Originalgröße zeigen

d.h. bei Multiplikation aller Variablen mit einem Faktor λ nimmt der Funktionswert den λ^r–fachen Wert an.

Spezialfall: Linearhomogenität (Homogenität vom Grade 1).

2. Bedeutung: Homogene, v.a. linear-homogene Funktionen, finden in Produktions- und Kostentheorie, Nutzentheorie, Haushaltstheorie und Wachstumstheorie Verwendung.

Beispiele:
(1) Homogene Produktionsfunktionen implizieren bei konstanten Faktorpreisverhältnissen konstante Einsatzverhältnisse der Produktionsfaktoren. Im Fall linear-homogener Produktionsfunktionen gilt daneben das Ertragsgesetz und bei zusätzlichem Vorliegen vollständiger Konkurrenz das Euler'sche Theorem.


(2) Linear-homogene Nutzenfunktionen beinhalten Freiheit von Geldillusion. Aus ihnen abgeleitete Einkommens-Konsumfunktionen haben Einkommenselastizitäten von 1, die in der Wachstumstheorie eine der Voraussetzungen für gleichmäßiges Wachstum (sog. evolutorische Wirtschaft) sind.