homogene Produktionsfunktion
GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
Übersicht
zuletzt besuchte Definitionen...
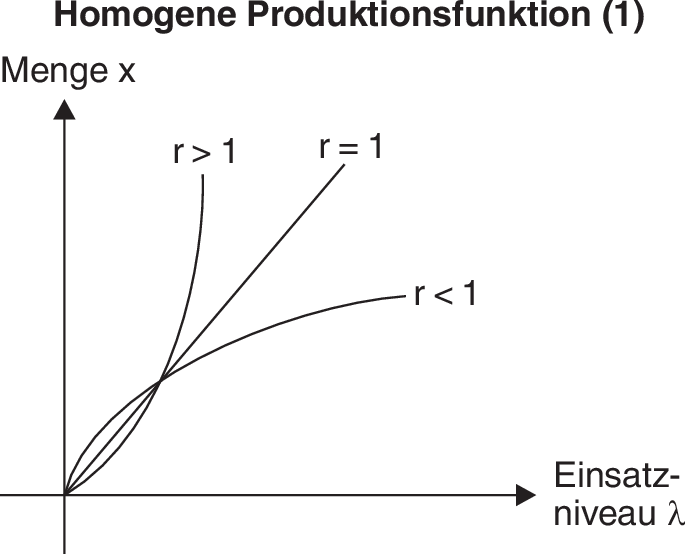
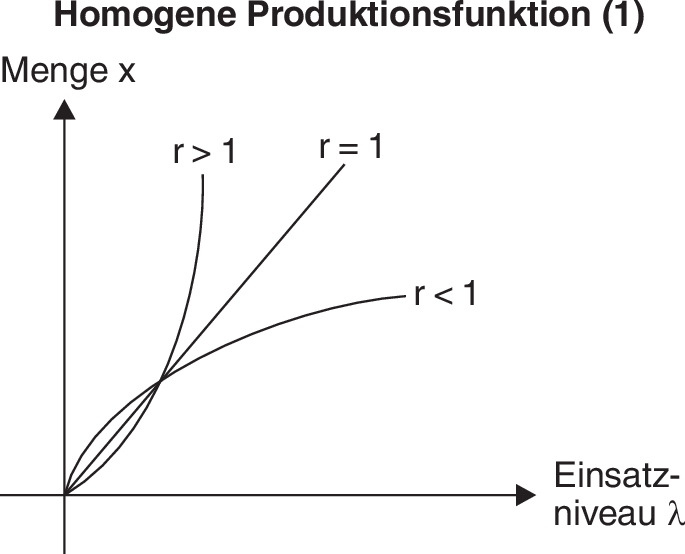
Spezielle Produktionsfunktion, die durch Homogenität charakterisiert ist: Wenn das Niveau des Faktoreinsatzes λ erhöht wird, erhöht sich die Ausbringungsmenge ebenfalls um das λ-fache. Dabei kann sich der Output proportional, unter- oder überproportional verändern, d.h., es liegen konstante, abnehmende oder steigende Skalenerträge vor (vgl. Abbildung „Homogene Produktionsfunktion (1)”).
Dieser Zusammenhang kann auch mithilfe der Skalenelastizität beschrieben werden. Ist diese durchweg konstant, liegen homogene Produktionsfunktionen vor. Letztere werden definiert durch die Bedingung:
f(
A, B) = r f(A, B).
Dabei bezeichnet r den Homogenitätsgrad. Man unterscheidet linear-homogene (r = 1), unterlinear-homogene (r < 1) und überlinear-homogene (r > 1) Produktionsfunktionen (Abbildung (1)). Im Fall r = 1 bedeutet dies, dass z.B. eine Verdoppelung aller eingesetzten Produktionsfaktormengen zu einer Verdoppelung des Outputs führt; ist r > 1, wächst der Output entsprechend stärker an, während sich im Fall r < 1 der Output weniger als verdoppelt.
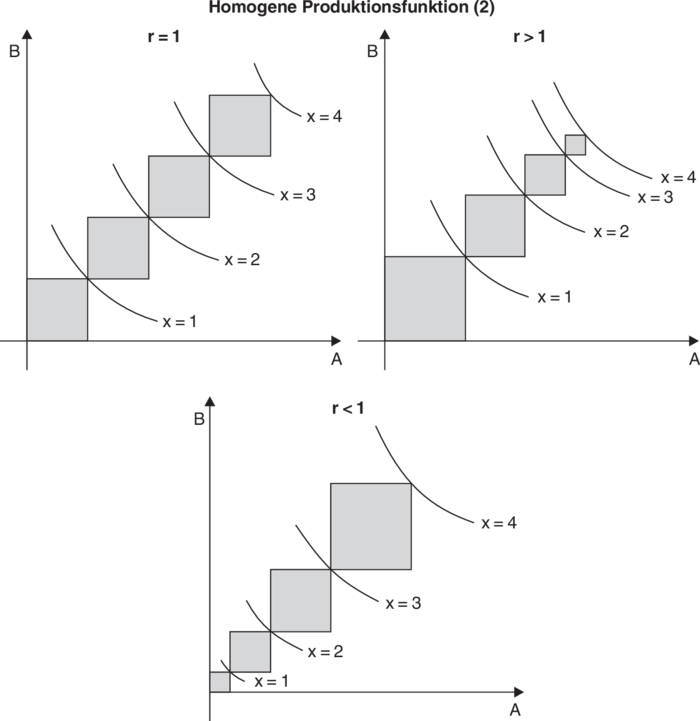
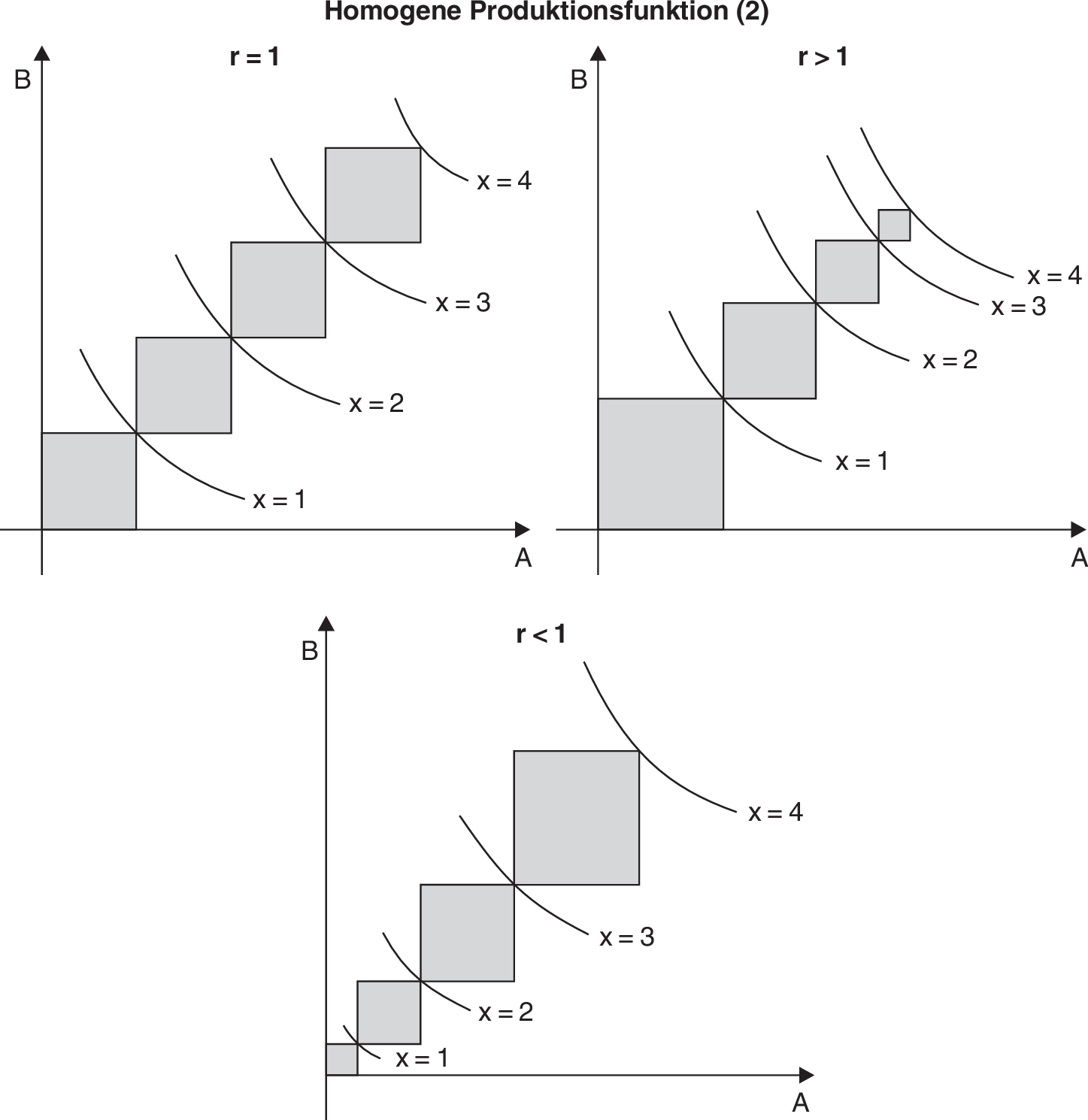
Man kann diesen Zusammenhang auch anhand des Isoquantensystems darstellen (vgl. Abbildung „Homogene Produktionsfunktion (2)”).
Erhöht man sukzessive das Output-Niveau jeweils um eine Einheit, so benötigt man das gleiche (r = 1), ein kleineres (r > 1) oder ein größeres (r < 1) „Faktorpäckchen”. Im Übrigen stimmt r mit der Skalenelastizität ηx,λ überein. Welcher Fall realiter eintritt, ist eine (empirische) Frage der Produktionstechnik bzw. der Organisation. Unmittelbar ersichtlich ist, dass ein Zusammenhang mit dem Verlauf der Kostenfunktion besteht.
Homogene Produktionsfunktionen besitzen die ökonomische Eigenschaft, dass die Grenzrate der Substitution (bzw. das Verhältnis der Grenzerträge) nur abhängig ist vom Verhältnis der Faktoreinsatzmengen. Im Fall r = 1 gilt dies auch für die Grenzerträge (∂x/∂A, ∂x/∂B) selbst. So folgt z.B. für die Wicksell-Cobb-Douglas-Produktionsfunktion
