Normalform

I. Spieltheorie:

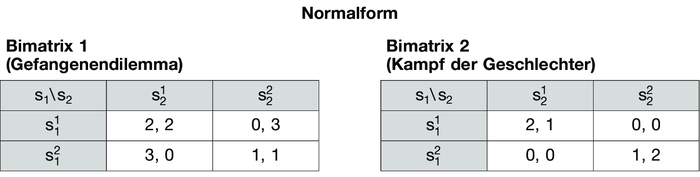
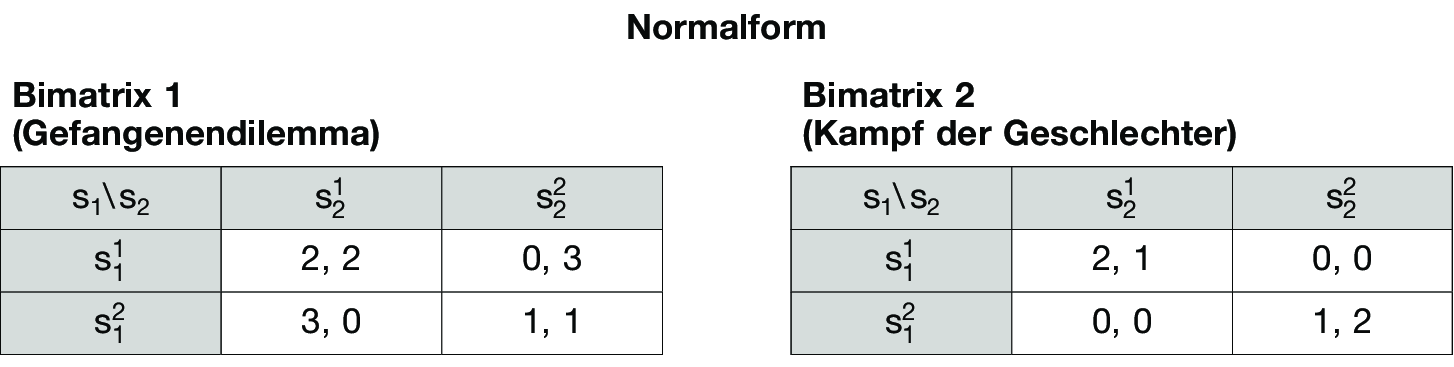
Die Normalform (S₁, ..., S_n; u₁, ..., u_n) eines n-Personen-Spiels mit den Spielern 1, ..., n beschreibt ein Spiel rein statisch. Für Spieler i = 1, ..., n bezeichnet S_i = {s_i¹, s_i², s_i³, ... }die Menge seiner Strategien s_i und u_i seine Auszahlungsfunktion. Allen Strategienvektoren s = (s₁, ..., s_n) mit s_i S_i für i = 1, ..., n ordnet die Auszahlungsfunktion u_i kardinale Nutzenwerte u_i(s) zu, die angeben, wie Spieler i die durch s implizierten Ergebnisse bewertet.

Bild in Originalgröße zeigen

– Bekannte Spiele mit zwei Spielern (n = 2), die über jeweils zwei Strategien verfügen, sind das Gefangenendilemma (vgl. Bimatrix 1 in der Abbildung „Normalform”) sowie der Kampf der Geschlechter (vgl. Bimatrix 2 in der Abbildung „Normalform”). Sind Spiele wie die Bimatrixspiele 1 und 2 symmetrisch, so genügt es, wegen u_i(s_i^k, s_j^l) = u_j(s_i^l, s_j^k) nur eine Nutzenbewertung anzugeben. Das Gleiche gilt für die sog. 2-Personen-Nullsummenspiele mit u₁(s) + u₂(s) = 0 für alle Strategievektoren s = (s₁, s₂), da u₂(s) =

u₁(s).

Vgl. auch Spieltheorie.

II. Wirtschaftsinformatik:

1. Begriff: In der Datenorganisation ein Zustand einer Relation (bzw. einer Datei), der i.Allg. durch Normalisierung erzeugt wird.

2. Arten: Man unterscheidet bis zur fünften Normalform. Die Normalformen bauen aufeinander auf; d.h. eine Relation in dritter Normalform ist automatisch auch in zweiter Normalform (und damit auch in erster Normalform) etc.; von praktischer Bedeutung ist v.a. die dritte Normalform.