Zitierfähige Version
- Revision von Lorenzkurve vom 19.02.2018 - 15:54
- Revision von Lorenzkurve vom 27.09.2017 - 14:53
- Revision von Lorenzkurve vom 18.08.2017 - 15:32
- Revision von Lorenzkurve vom 25.02.2013 - 13:08
- Revision von Lorenzkurve vom 25.11.2009 - 16:27
- Revision von Lorenzkurve vom 14.09.2009 - 13:55
- Revision von Lorenzkurve vom 05.06.2009 - 15:09
Lorenzkurve
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
zuletzt besuchte Definitionen...
Inhaltsverzeichnis
Statistik
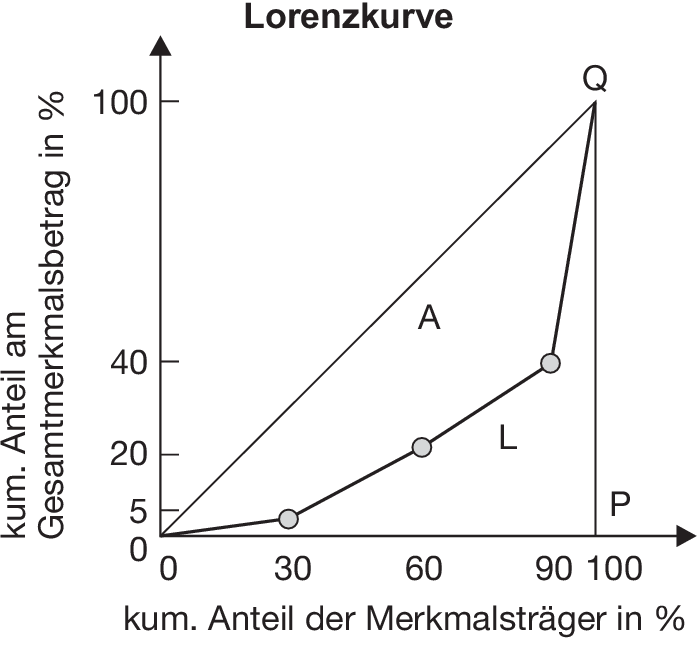
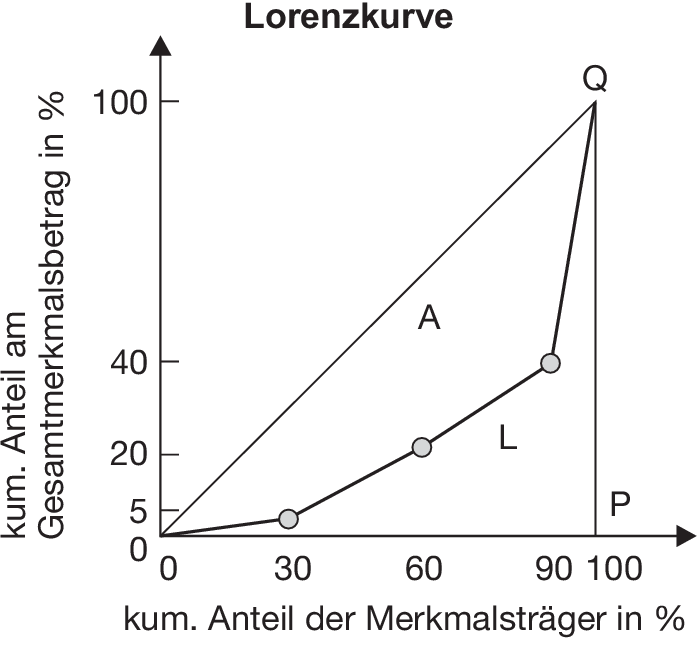
Sonderform der graphischen Darstellung einer Häufigkeitsverteilung, die v.a. die relative Konzentration veranschaulicht. Für jede Klassengrenze wird in einem Koordinatensystem ein Punkt eingezeichnet, dessen Abszisse die kumulierte relative Häufigkeit der Merkmalsträger und dessen Ordinate der kumulierte relativierte Gesamtmerkmalsbetrag ist. Diese werden geradlinig verbunden. Die Lorenzkurve bietet Informationen folgender Art: Die x Prozent der „kleineren” Merkmalsträger vereinigen (nur) y Prozent des Gesamtmerkmalsbetrages auf sich.
Beispiel: Die Häufigkeitsverteilung von Einkommen gemäß Tabelle „Lorenzkurve - Wertebeispiel” dargestellt ergibt die in der Graphik „Lorenzkurve” dargestellte Lorenzkurve.
Die Gerade OQ wird als Gleichverteilungsgerade bezeichnet, da sie als Lorenzkurve entsteht, wenn alle Merkmalsträger denselben Merkmalswert haben. Je größer die Fläche A ist, umso größer ist die relative Konzentration. Der Anteil von A an der Fläche des Dreiecks OPQ, der 2 A beträgt, entspricht dem Gini-Koeffizienten.
Verteilungstheorie
Die Lorenzkurve ist die gebräuchlichste Form der Veranschaulichung von Einkommensverteilungen. Man erhält die Lorenzkurve, wenn man die Einkommensbezieher nach der Höhe ihres Einkommens ordnet und sie dann, beginnend mit den unteren und fortschreitend zu den oberen Einkommensbeziehern zu Gruppen von jeweils x Prozent der Bevölkerung zusammenfasst. Anschließend wird ermittelt, wie viel x Prozent des Volkseinkommens auf jede Gruppe entfallen. In der Lorenzkurve sind die kumulierten Anteile erfasst, so dass man für jeden Prozentsatz der Bevölkerung den auf sie entfallenden Anteil am Volkseinkommen angeben kann. Die Einkommensverteilung ist um so gleichmäßiger, je mehr sich die Lorenzkurve der 45°-Linie nähert. Die 45°-Linie entspricht der Gleichverteilung, da dann x Prozent der Bevölkerung auch einen Anteil am Nationaleinkommen von x Prozent erhalten.
Vgl. auch personelle Einkommensverteilung, Gini-Koeffizient, Lorenz-Halbordnung.

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon