neoklassische Produktionsfunktion

1. Begriff: Ertragsgesetzliche Produktionsfunktion mit von Anfang an abnehmenden Grenzerträgen (s. Ertragsgesetz).

2. Eigenschaften: a) Bei totaler Faktorvariation weist die neoklassische Produktionsfunktion konstante oder abnehmende Skalenerträge auf.

b) Bei partieller Faktorvariation zeigen sich positive, nicht-zunehmende (bzw. abnehmende) Grenzerträge.

c) Die Isoquante ist monoton fallend und konvex mit einer abnehmenden Grenzrate der Substitution.

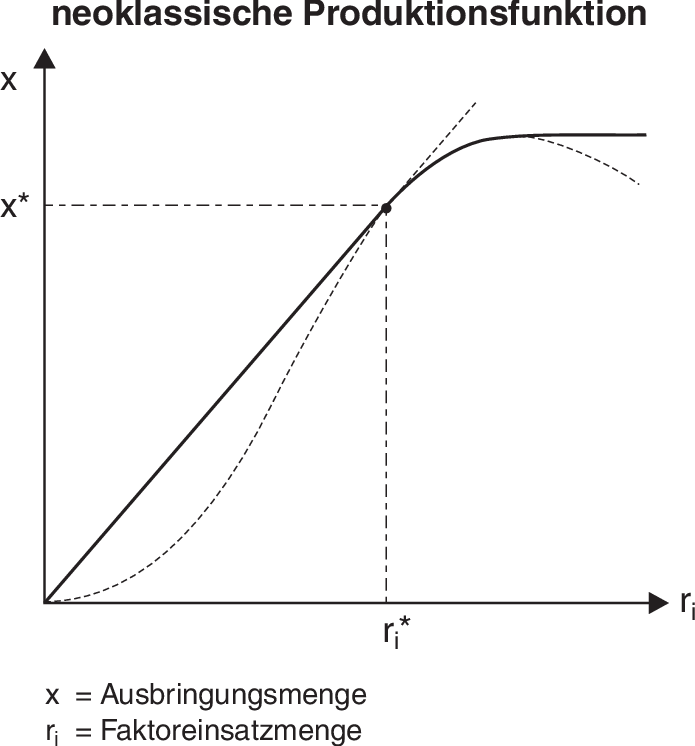
3. Entwicklung: Die neoklassische Produktionsfunktion ergibt sich aus der klassischen Produktionsfunktion, indem man (wie in der Abbildung „Neoklassische Produktionsfunktion” dargestellt) deren ineffiziente Bereiche (Effizienz) durch geeignete Konvexkombinationen ausgewählter Produktionspunkte ersetzt. So wird der konvexe Bereich der klassischen Produktionsfunktion durch Konvexkombination der Nullaktivität (Aktivität) und des Punkts (r_i*, x*), an dem ein Fahrstrahl an die Kurve zur Tangente wird, dominiert. Der vierte Bereich des klassischen Ertragsgesetzes mit abnehmendem Gesamtertrag wird durch eine Disposal-Aktivität dominiert, bei der die überschüssigen Faktormengen nicht eingesetzt werden.

Bild in Originalgröße zeigen

4. Beurteilung: Obwohl die neoklassische Produktionsfunktion ein theoretisches Konstrukt ist, hat sie sich in vielen Anwendungsbereichen sowohl auf gesamt- als auch auf einzelwirtschaftlicher Ebene empirisch bewährt. Ihre Eigenschaften lassen sich in späteren Ansätzen der Produktionstheorie immer wieder nachweisen.