Zitierfähige Version
Unter dieser URL finden Sie dauerhaft die unten aufgeführte Version Ihrer Definition:
Revision von Wahrscheinlichkeitsnetz vom 30.07.2009 - 14:41
- Revision von Wahrscheinlichkeitsnetz vom 05.06.2009 - 15:10
- Revision von Wahrscheinlichkeitsnetz vom 30.07.2009 - 14:41
- Revision von Wahrscheinlichkeitsnetz vom 09.10.2009 - 09:50
- Revision von Wahrscheinlichkeitsnetz vom 24.02.2010 - 15:55
- Revision von Wahrscheinlichkeitsnetz vom 18.01.2013 - 12:25
- Revision von Wahrscheinlichkeitsnetz vom 18.08.2017 - 16:19
- Revision von Wahrscheinlichkeitsnetz vom 16.02.2018 - 15:59
Wahrscheinlichkeitsnetz
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
zuletzt besuchte Definitionen...
Ausführliche Definition im Online-Lexikon
Hilfsmittel zur schnellen (und nicht ganz objektiven) Prüfung der Hypothese, eine Grundgesamtheit weise eine Normalverteilung auf, sowie ggf. zur schnellen Ermittlung von Schätzwerten  und
und  für deren Parameter μ und σ anhand eines Stichprobenbefundes.
für deren Parameter μ und σ anhand eines Stichprobenbefundes.
1. Konstruktion des Wahrscheinlichkeitsnetzes: Ein Wahrscheinlichkeitsnetz entsteht dadurch, dass die Ordinatenwerte eines Koordinatensystems durch die korrespondierenden Werte der Verteilungsfunktion der Standardnormalverteilung ersetzt werden. Damit wird die Verteilungsfunktion jeder Normalverteilung zu einer Geraden.
2. Prüfung einer Verteilungshypothese: Werden über den Merkmalswerten (nicht klassierte Daten) oder Klassenobergrenzen (klassierte Daten, Klassenbildung) die zugehörigen kumulierten relativen Häufigkeiten aus einer Stichprobe (Teilerhebung) im Wahrscheinlichkeitsnetz abgetragen und ergibt sich eine ungefähr lineare Anordnung der resultierenden Punkte, so besteht Grund zu der Annahme, die Grundgesamtheit sei normalverteilt.
3. Parameterschätzung: Gleicht man diese Punkte visuell durch eine Gerade aus, so kann man mit ihrer Hilfe Schätzwerte und
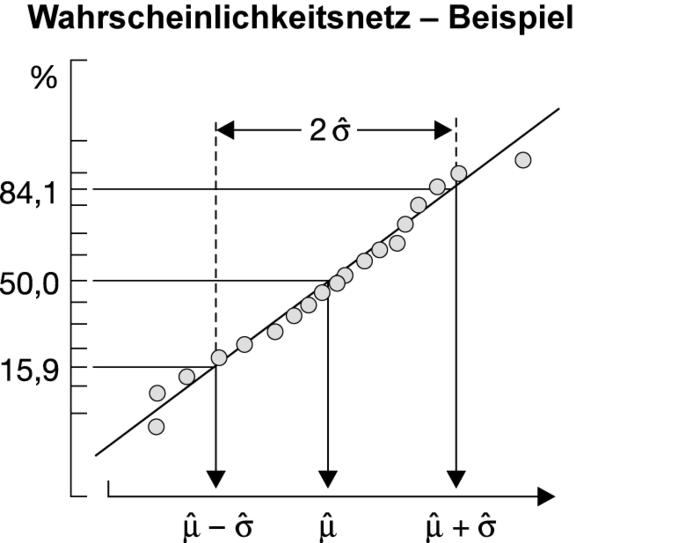
und  für die entsprechenden Parameter ermitteln. Hierzu geht man bei den Ordinaten 50 Prozent, 15,87 Prozent und 84,13 Prozent in das Wahrscheinlichkeitsnetz ein (vgl. Abbildung „Wahrscheinlichkeitsnetz
für die entsprechenden Parameter ermitteln. Hierzu geht man bei den Ordinaten 50 Prozent, 15,87 Prozent und 84,13 Prozent in das Wahrscheinlichkeitsnetz ein (vgl. Abbildung „Wahrscheinlichkeitsnetz
Beispiel”). Der zur Ordinate 50 Prozent gehörende Abszissenwert ist ; subtrahiert man die Abszissenwerte, die zu den Ordinaten 84,13 bzw. 15,87 gehören, voneinander und halbiert die Differenz, so erhält man damit
; subtrahiert man die Abszissenwerte, die zu den Ordinaten 84,13 bzw. 15,87 gehören, voneinander und halbiert die Differenz, so erhält man damit  .
.
1. Konstruktion des Wahrscheinlichkeitsnetzes: Ein Wahrscheinlichkeitsnetz entsteht dadurch, dass die Ordinatenwerte eines Koordinatensystems durch die korrespondierenden Werte der Verteilungsfunktion der Standardnormalverteilung ersetzt werden. Damit wird die Verteilungsfunktion jeder Normalverteilung zu einer Geraden.
2. Prüfung einer Verteilungshypothese: Werden über den Merkmalswerten (nicht klassierte Daten) oder Klassenobergrenzen (klassierte Daten, Klassenbildung) die zugehörigen kumulierten relativen Häufigkeiten aus einer Stichprobe (Teilerhebung) im Wahrscheinlichkeitsnetz abgetragen und ergibt sich eine ungefähr lineare Anordnung der resultierenden Punkte, so besteht Grund zu der Annahme, die Grundgesamtheit sei normalverteilt.
3. Parameterschätzung: Gleicht man diese Punkte visuell durch eine Gerade aus, so kann man mit ihrer Hilfe Schätzwerte
Beispiel”). Der zur Ordinate 50 Prozent gehörende Abszissenwert ist

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon