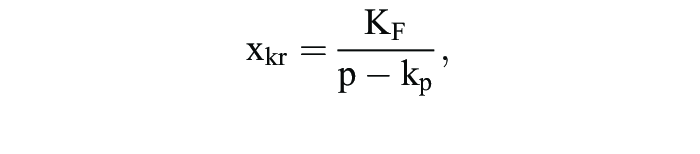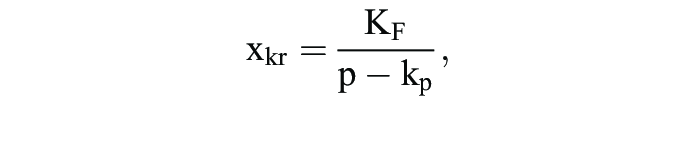Zitierfähige Version
- Revision von Break-Even-Analyse vom 15.02.2018 - 15:01
- Revision von Break-Even-Analyse vom 14.09.2017 - 17:27
- Revision von Break-Even-Analyse vom 29.01.2013 - 12:44
- Revision von Break-Even-Analyse vom 16.11.2009 - 11:11
- Revision von Break-Even-Analyse vom 07.09.2009 - 18:10
- Revision von Break-Even-Analyse vom 23.06.2009 - 12:13
Break-Even-Analyse
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
zuletzt besuchte Definitionen...
I. Kostenrechnung:
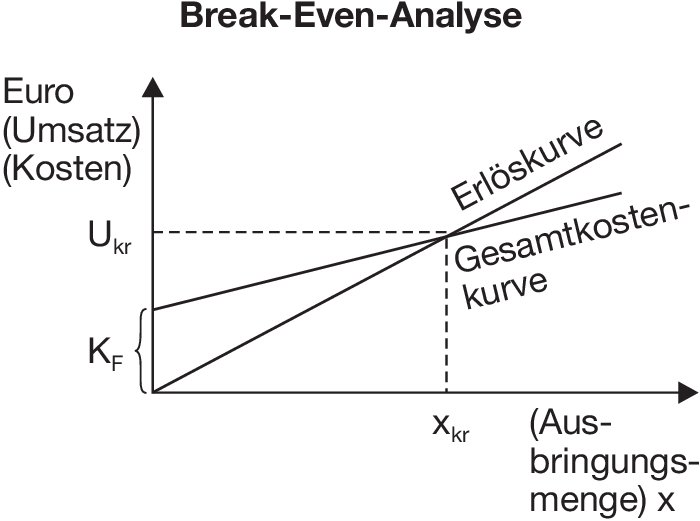
1. Begriff: Ermittlung desjenigen Gesamtumsatzes eines Produkts, Bereichs oder Unternehmens, dessen Unterschreiten zu Verlusten, dessen Überschreiten zu Gewinnen führt (Deckungsumsatz). Im Break-Even-Point (Deckungs-, Gewinnpunkt, Gewinn-, Kostenschwelle, „Toter Punkt”) ist die Summe aus fixen Kosten und variablen Kosten gleich dem Gesamterlös (Erlöse).
2. Ermittlung: Angenommen werden gleichbleibende fixe Kosten, zur Veränderung des Umsatzes proportional verlaufende variable Kosten, konstante Preise.
a) Einproduktfall:(1) Für den mengenmäßigen Gewinnpunkt xkr gilt:
wobei: p = Preis, x = umgesetzte Menge, kp = proportionaler Selbstkostenpreis pro Stück, KF = fixe Kosten.
(2) Für den umsatzmäßigen Gewinnpunkt Ukr gilt:
b) Mehrproduktfall: In Mehrproduktunternehmen gibt es eine Vielzahl von Absatzmengenkombinationen, die zum Gewinnpunkt führen. Daher ist die Ermittlung eines Deckungsumsatzes nur unter der Voraussetzung konstanter Zusammensetzung des Umsatzes möglich.
3. Bedeutung/Anwendung: Instrument der produkt-, bereichs- oder gesamtunternehmensbezogenen Gewinnplanung und -kontrolle. Die Break-Even-Analyse dient als Entscheidungshilfe für das Management.
II. Investitionsrechnung:
Ermittlung des Zeitpunktes, in dem die Summe der durch eine Investition verursachten Einzahlungen erstmals die Summe der durch die Investition verursachten Auszahlungen übersteigt.
Vgl. auch Amortisationsrechnung.

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon