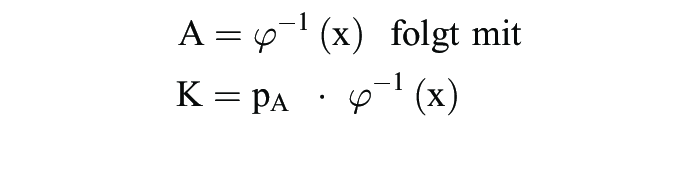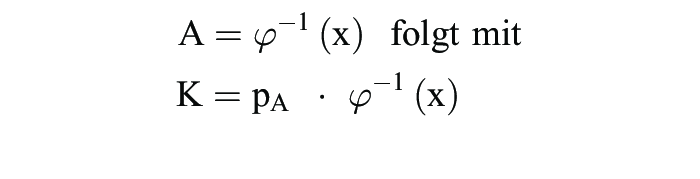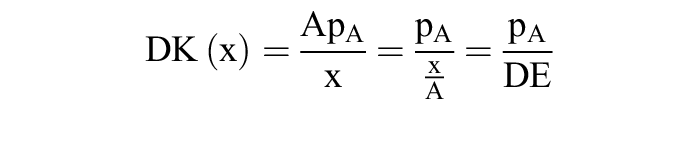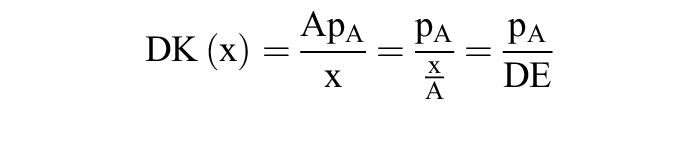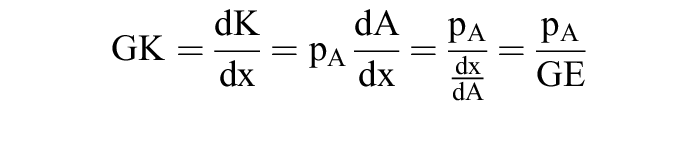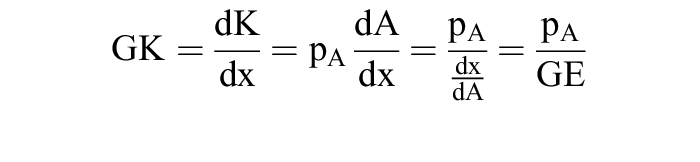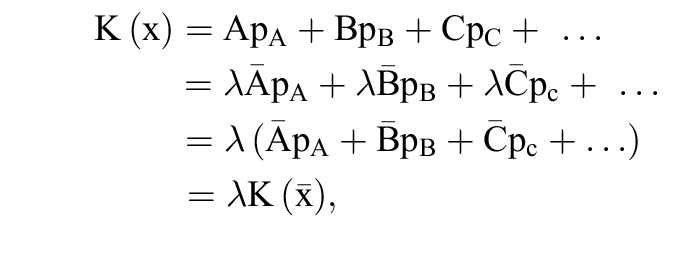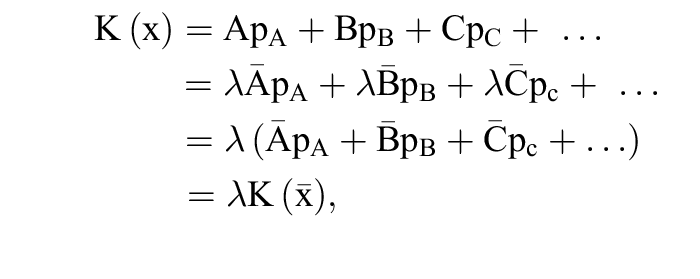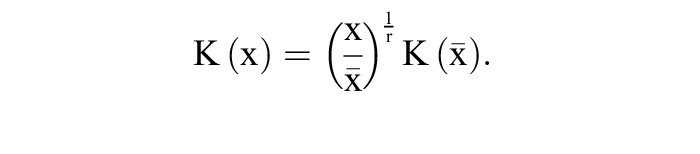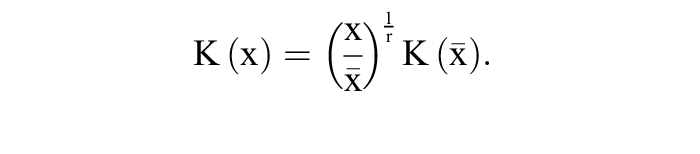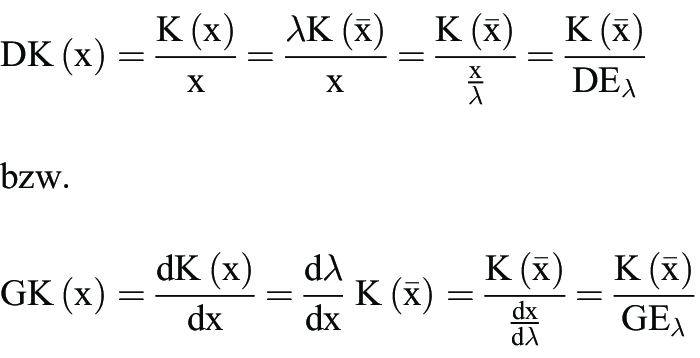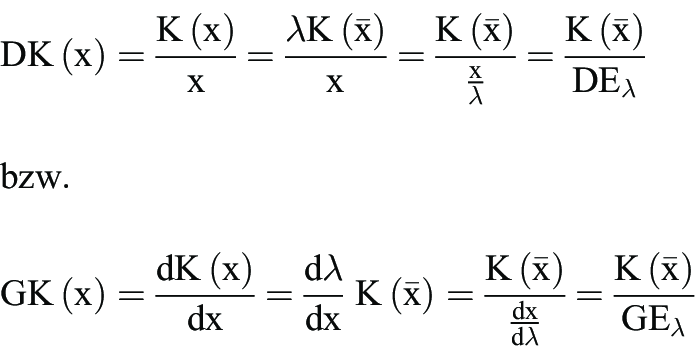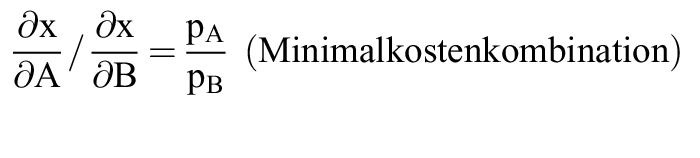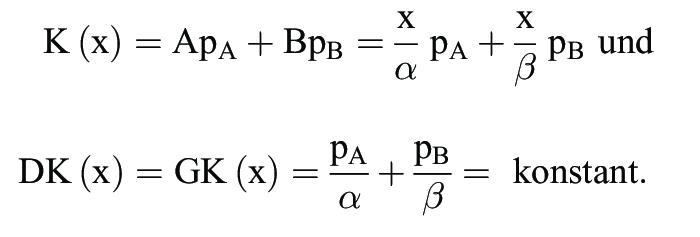Kostenfunktion, Herleitung aus der Produktionsfunktion

1. Allgemein: a) Die Produktionstheorie bildet die Grundlage, um verschiedene Kostenverläufe zu erklären. Der Zusammenhang lässt sich verdeutlichen, wenn man zunächst auf nur einen Produktionsfaktor A abstellt: x = φ (A). Es gilt definitorisch K(x) = p_A · A (p_A = Lohnsatz, A = Arbeitsmenge). Wegen

Bild in Originalgröße zeigen

der behauptete Zusammenhang. Daraus ergibt sich auch die Beziehung zwischen Durchschnittskosten und Durchschnittsertrag einerseits, von Grenzkosten und Grenzertrag andererseits. Aus K(x) = p_A · A folgt:

Bild in Originalgröße zeigen

(mit DE = Durchschnittsertrag), ebenso gilt:

Bild in Originalgröße zeigen

(GE = Grenzertrag). Man sieht, dass DK bzw. GK fallen, steigen oder konstant bleiben müssen, wenn DE bzw. GE steigen, fallen oder konstant sind, d.h. es handelt sich, bei konstantem Lohnsatz, jeweils um reziproke Größen. Das heißt zugleich, dass den Maxima der Grenz- bzw. Durchschnittserträge die Minima der Grenz- bzw. Durchschnittskosten entsprechen. Die Kostenverläufe sind damit auf die Ertragsverläufe zurückführbar.

b) Bei mehr als einem Produktionsfaktor (A, B, ...) kann man die Kostenfunktion

K(x) = A pA + B pB + ...

Bild in Originalgröße zeigen

Bild in Originalgröße zeigen

Für r = 1, r < 1 und r > 1 erhält man jeweils die Verläufe a), b) und c). Dies ergibt sich auch aus den Gleichungen

Bild in Originalgröße zeigen

wobei DE_λ und GE_λ für das Niveaudurchschnitts- und Niveaugrenzprodukt stehen.

4. Der Fall der isoquanten Faktorvariation wird relevant, wenn sich infolge einer Änderung der relativen Faktorpreise die Minimalkostenkombination ändert. Damit wird die Verschiebung der Kostenfunktion als Folge dieser Preisänderung erklärt. Für je zwei Faktoren muss

Bild in Originalgröße zeigen

gelten, was hier zu einer Beziehung zwischen A und B führt, mit deren Hilfe aus der Definitionsgleichung K = A p_A + B p_B und der Produktionsfunktion x = F(A, B) die Kostenfunktion K(x) bestimmt werden kann. Entsprechend ergibt sich auch die neue Kostenfunktion nach einer Änderung der Faktorpreisrelation.

5. Bei der Leontief-Produktionsfunktion kommt nur die proportionale Faktorvariation in Betracht, weil das Einsatzverhältnis der Faktoren konstant ist. Wegen (x = αA; x = βB) ergibt sich in diesem Fall (α, β = konstant)

Bild in Originalgröße zeigen