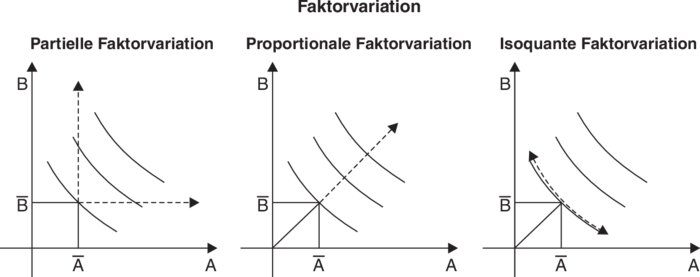
Faktorvariation

1. Gibt man unterschiedliche Produktionsniveaus vor, erhält man definitionsgemäß unterschiedliche Isoquanten. Sie zeigen eine um so höhere Produktmenge an, je weiter sie vom Ursprung entfernt sind. Sie schneiden sich auch nicht. Isoquanten, die eine größere Menge repräsentieren, werden durch höheren Einsatz von A und/oder B erreicht, falls die Faktoren substituierbar sind. Ausgehend vom Faktoreinsatz (, ) und der Produktmenge können Isoquanten mit höherem Produktionsniveau erreicht werden, wenn entweder eine partielle Faktorvariation (Erhöhung von A bei Konstanz von B = oder umgekehrt Erhöhung von B bei Konstanz von A = ) oder eine totale Faktorvariation vorgenommen wird. Im letzteren Fall werden beide Faktoreinsatzmengen zugleich verändert.

Bild in Originalgröße zeigen

Wichtig sind hier die beiden Unterfälle der proportionalen und der isoquanten Faktorvariation (vgl. Abbildung „Faktorvariation”).

a) Bei der ersteren werden die Faktoren im gleichen Verhältnis erhöht (oder vermindert). Bei limitationalen Produktionsfaktoren kommt nur diese Art der Faktorvariation in Betracht. Isoquante Faktorvariation bedeutet eine Bewegung entlang einer Isoquante (konstante Produktmenge), woraus die Bezeichnung resultiert.

b) Die partielle Faktorvariation wird vorgenommen, wenn der (die) andere(n) Faktor(en) nicht beschafft werden kann (können) oder man z.B. abwartet, ob der Anstieg der Nachfrage auch dauerhaft ist, zwischenzeitlich behilft man sich etwa mit Überstunden.

c) Proportionale Faktorvariation - praktisch eine Variation der Betriebsgröße - wird bei steigender Nachfrage vorgenommen, wenn die (erwarteten) Faktorpreise unverändert bleiben. Eine isoquante Faktorvariation wird realisiert, wenn das Faktorpreisverhältnis sich ändert (Minimalkostenkombination).

2. Formal lässt sich bei partieller Faktorvariation die Produktmenge x allein in Abhängigkeit vom variierten Faktoreinsatz (im Beispiel A) darstellen:

x = F(A, B, C, ...)

wird zu

x = F(A, , , ...) = f(A).

Im Fall proportionaler Faktorvariation kann die Produktmenge x als Funktion des Einsatzniveaus λ dargestellt werden: Aus A = und B = folgt:

x = F(A, B) = f(, ) = f().

Daraus können der Grenzertrag (partielles Grenzprodukt) x /A bzw. x /B einerseits (Ertragsgesetz), das Niveaugrenzprodukt dx /d andererseits bestimmt werden. Der partiellen Faktorvariation ist die Produktionselastizität, der proportionalen die Skalenelastizität und der isoquanten die Substitutionselastizität zugeordnet.

Bei der isoquanten Faktorvariation ergibt sich aus der Produktionsfunktion die Gleichung der Isoquante:

Die Isoquante lässt sich auch mithilfe der Formel für das totale Grenzprodukt,

(diese gilt für alle Faktorvariationen), beschreiben, und zwar durch die Bedingung dx = 0, was zu

führt (Minimalkostenkombination), d.h. die Grenzrate der Substitution ist als das Verhältnis der Grenzerträge darstellbar.