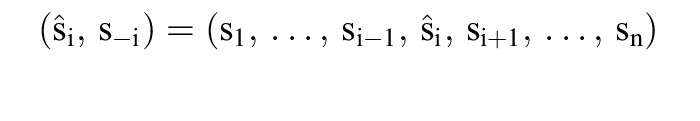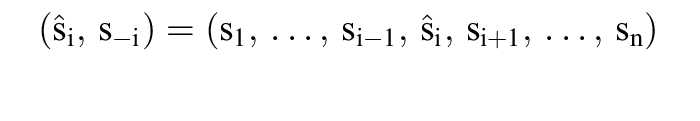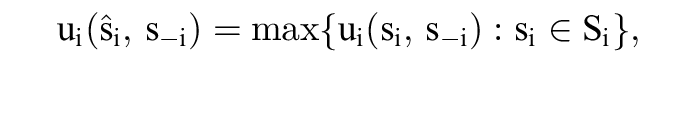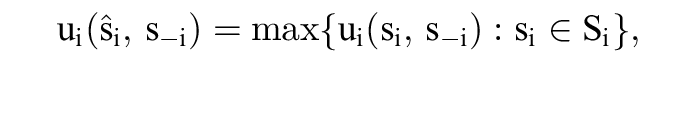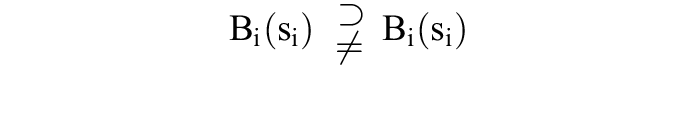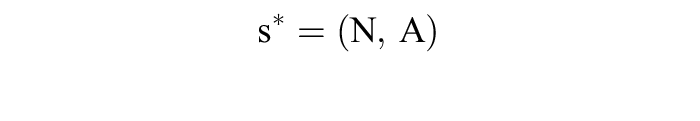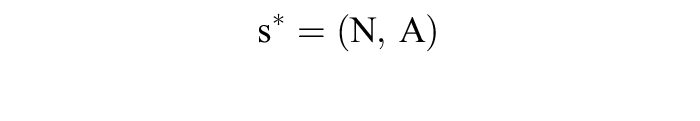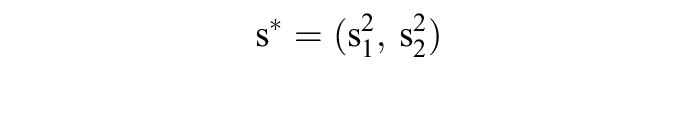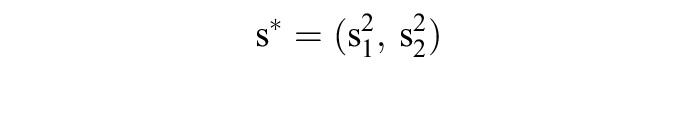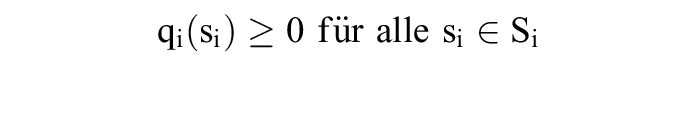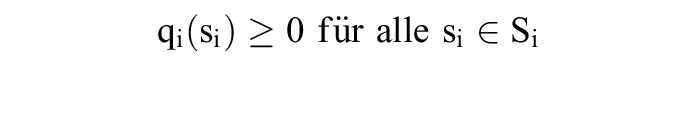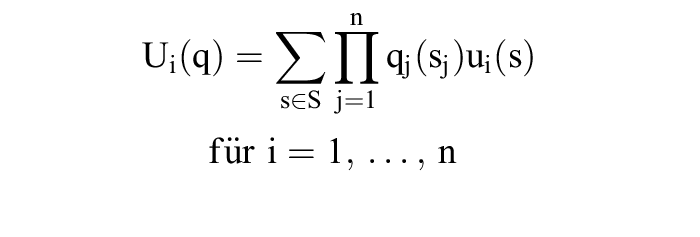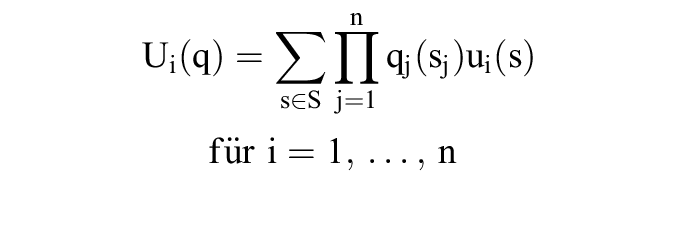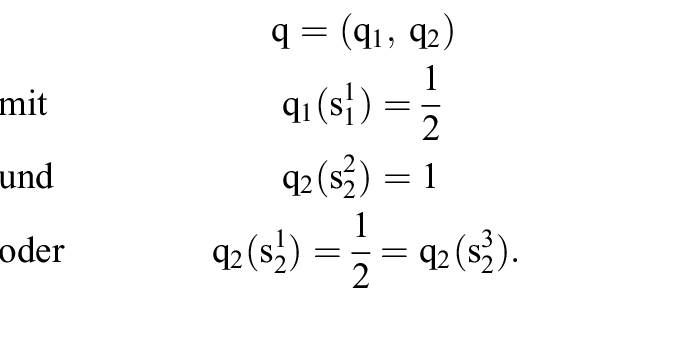Spieltheorie

I. Begriff und Entwicklung

Die Spieltheorie ist eine mathematische Methode, die das rationale Entscheidungsverhalten in sozialen Konfliktsituationen ableitet, in denen der Erfolg des Einzelnen nicht nur vom eigenen Handeln, sondern auch von den Aktionen anderer abhängt. Der Begriff „Spieltheorie” beruht darauf, dass am Anfang der mathematischen Spieltheorie den Gesellschaftsspielen wie Schach, Mühle, Dame etc. große Aufmerksamkeit gewidmet wurde. Frühe ökonomische Beiträge zur Spieltheorie wurden von Cournot und Edgeworth verfasst.

Als Meilenstein für die Entwicklung der Spieltheorie erwies sich das Buch von Neumann und Morgenstern. Danach hat sich die Spieltheorie erst allmählich und seit 1970 überaus stürmisch als die beherrschende Methodik in den

traditionell normativ ausgerichteten

Wirtschaftswissenschaften sowie mehr und mehr auch in den sozialwissenschaftlichen Nachbardisziplinen durchgesetzt. Der Nobelpreis für Wirtschaftswissenschaften des Jahres 1994, der an Harsanyi, Nash und Selten in Anerkennung ihrer Verdienste um die Weiterentwicklung der Spieltheorie vergeben wurde, verdeutlicht die überragende Bedeutung der Spieltheorie für die moderne Wirtschaftstheorie.

Als wichtige (Lehr-)Bücher nach von Neumann und Morgenstern wurden v.a. Luce und Raiffa sowie Owen weithin geschätzt. Heute gibt es eine Fülle an Einführungen zur Spieltheorie, die kaum noch zu überblicken ist. Als deutsche Lehrbücher bieten sich die Werke von Berninghaus, Güth sowie Holler und Illing an.

II. Lösungskonzepte

Lösungskonzepte sollen das individuell rationale Verhalten in strategischen Entscheidungssituationen definieren. Der Tradition der Spieltheorie entsprechend werden Spiele mathematisch exakt beschrieben, so dass eine strenge mathematische Lösng möglich ist. Wird ein Spiel nur durch seine charakteristische Funktion erfasst, so kann natürlich nicht das individuelle Verhalten selbst, sondern nur die Auszahlungsaufteilung beschrieben werden. Im Folgenden wird daher von Spielen in extensiver Form oder in Normalform ausgegangen. In derartigen Spielen sollte eine Lösungskonzeption diejenigen Strategien der Spieler auszeichnen, die den intuitiven Anforderungen an rationales Entscheiden genügen. Geht man von der extensiven Form eines Spiels aus, so muss eine Strategie s_i  S_i eines Spielers i für jeden Informationsbezirk einen Zug auswählen.

 

1.Dominierte und inferiore Strategien

Für einen Strategievektor s = (s₁, ..., s_n) eines n-Personen-Spiels sei s_-i = (s₁, ..., s_i-1, s_i+1, ..., s_n) der n-1-Vektor ohne i-te Komponente und

der Strategievektor bestehend aus @scirc;_i und s_-i. Eine Strategie s_i heißt dominiert, falls Spieler i über eine alternative Strategie @scirc;_i verfügt, für die u_i (@scirc;_i, s_-i) ≥ u_i (s_i, s_-i) für alle Vektoren s_-i mit strikter Ungleichung für wenigstens einen Vektor s_-i gilt. In der Abbildung „Extensive Form

Vertrauensspiel” (extensive Form) ist die Strategie s₂ = G von Spieler 2 dominiert, da r > s; in der Abbildung „Agentennormalform

Outside Option-Spiel” (Agentennormalform) ist die Strategie s₁ = (R₁, l₁) von Spieler 1 dominiert, da z.B. @scirc;₁ = (L₁, l₁) die obige Bedingung erfüllt. Dominierte Strategien sollte ein Spieler vermeiden, da es alternative Strategien gibt, die niemals schlechter, aber manchmal besser sind, also das Risiko einer falschen Entscheidung verringern.

Vermeiden alle Spieler ihre dominierten Strategien und ist allgemein bekannt, dass alle dominierten Strategien vermieden und damit eliminiert werden, so können sich neue Strategien als dominiert erweisen.

Gilt

so wird @scirc;_ibeste Antwort auf s_-i genannt. Eine Strategie s_i heißt inferior, falls eine andere Strategie „häufiger” beste Antwort ist: Bezeichnet B_i(s_i) die Menge der Vektoren s_-i, auf die s_i beste Antwort ist, so ist s_i inferior, falls eine Strategie @scirc;_i existiert mit

,

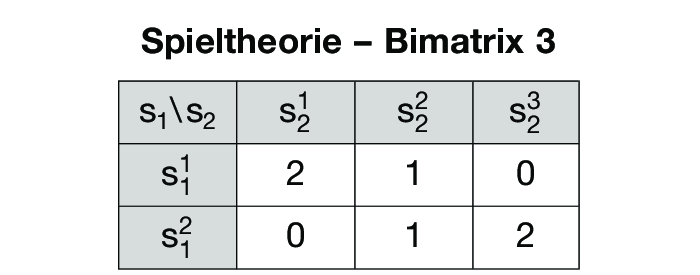
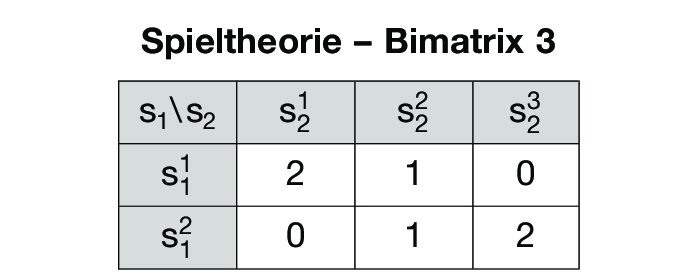
d.h. @scirc;_i ist immer beste Antwort, falls das für s_i zutrifft, aber nicht umgekehrt. Inferiore Strategien müssen nicht dominiert sein, wie folgendes 2-Personen Nullsummenspiel beweist, das nur durch die Auszahlungen u₂(s) für alle sechs Strategievektoren s = (s₁, s₂) beschrieben werden kann:

Obwohl nur s₂¹ beste Antwort auf s₁¹ und nur s₂³ beste Antwort auf s₁² ist, erweist sich die Strategie s₂² als undominiert.

Individuelle Rationalität verlangt, dass ein Spieler i an das Verhalten s_-i seiner Mitspieler optimal angepasst ist. Inferiore Strategien sind fragwürdig, weil es andere Strategien gibt, die sich auf vielfältige Verhaltensweisen s_-i als beste Antwort erweisen. Sie sollten daher als Lösungsstrategien ausscheiden und

ähnlich wie dominierte Strategien

wiederholt eliminiert werden.

 

2.Gleichgewichte

Der Begriff des Gleichgewichts ergibt sich aus den Anforderungen, dass erstens alle Spieler beste Antworten auf das Verhalten der Mitspieler auswählen und dass zweitens die Erwartungen bez. des Verhaltens der Mitspieler stets rational sind. Ein Gleichgewicht ist damit ein (Strategien-)Vektor

wechselseitig bester Antworten, d.h. für alle Spieler i = 1, ..., n des n-Personen-Spiels muss gelten, dass u_i (s*) ≥ u_i (s_i, s_-i) für alle Strategien s_i S_i von Spieler i gilt. Würde ein Strategievektor s allgemein erwartet, der ungleichgewichtig ist, so würde sich diese Erwartung offenbar selbst zerstören, da dann mindestens ein Spieler mehr verdienen würde, falls er von s abweicht. Man kann daher Gleichgewichte

und nur diese!

als selbstbestätigende allgemeine Verhaltenserwartungen charakterisieren.

Andere Begründungen für das Gleichgewicht basieren auf einleuchtenden Axiomen (z.B. dem (umgekehrten) Konsistenzaxiom, das auch dann einen Anreiz für Gleichgewichtsverhalten postuliert, wenn andere schon ihre Gleichgewichtsstrategie gewählt haben) sowie auf Anpassungsprozessen wie etwa der besten Antwortdynamik, die schon von Cournot verwandt wurde, oder

mit wechselhaftem Erfolg

Prozessen sozialen Lernens oder kultureller Evolution.

In der Abbildung „Extensive Form

Vertrauensspiel” (extensive Form) ist

das einzige Gleichgewicht; in Bimatrix 1 (Normalform) ist

eindeutiges Gleichgewicht, während in Bimatrix 2 (Normalform) sowohl als auch gleichgewichtig sind. Im Nullsummenspiel der Bimatrix 3 erweist sich hingegen kein Strategienvektor s = (s₁, s₂) als gleichgewichtig.

Um die Nichtexistenz von Gleichgewichten wie im Matrixspiel 3 zu vermeiden, erweitert man die strategischen Möglichkeiten der Spieler. Betrachtet sei eine Normalform (S₁, ..., S_n; u₁, ..., u_n), für die alle Strategienmengen S_i endlich sind. Für alle s_i in S_i sei q_i(s_i) die Wahrscheinlichkeit, mit der Spieler i die Strategie s_i verwendet. Eine gemischte Strategie q_i von Spieler i = 1, ..., n ist eine Wahrscheinlichkeitsverteilung über S_i, d.h.

und .

Da alle Spieler j = 1, ..., n ihr Verhalten unabhängig voneinander randomisieren, ist die Realisationswahrscheinlichkeit eines Strategievektors s durch bestimmt. Bezeichnet q = (q₁, ..., q_n) einen Vektor gemischter Strategien, Q_i die Menge gemischter Strategien q_i des Spielers i = 1, ..., n und S die Menge der Strategievektoren s, so ist die gemischte Erweiterung von (S₁, ..., S_n; u₁, ..., u_n) durch die Normalform (Q₁, ..., Q_n; U₁, ..., U_n) mit den Auszahlungsfunktionen

bestimmt. Gemäß der wichtigen Existenzaussage von Nash verfügt jede derartige gemischte Erweiterung über mindestens ein Gleichgewicht und jedes symmetrische Spiel dieser Art über mindestens ein symmetrisches Gleichgewicht. Die gemischte Erweiterung des Matrixspiels 3 verfügt über die Gleichgewichte

3. Verfeinerungen und Auswahl von Gleichgewichten

Das Problem der spieltheoretischen Lösungksonzepte ist häufig nicht die Existenz von Gleichgewichten, sondern eine Vielfalt. Um die Vielfalt einzuschränken, wurde der Gleichgewichtsbegriff verfeinert. Für extensive Spiele hat Selten gefordert, nur solche Gleichgewichte als Lösung zu akzeptieren, deren Handlungsanweisungen für jedes Teilspiel ein Gleichgewicht darstellen (Teilspielperfektheit). Das Konzept perfekter Gleichgewichte erfordert eine Robustheit der Anweisungen bezüglich kleiner Perturbationen, die man anschaulich auch als „zitternde Hand” bei der Strategienwahl beschreiben kann.

Das zur Perfektheit nahezu identische Konzept sequenzieller Gleichgewichte verzichtet

wenn auch nur vordergründig

auf Zittern bei der Strategienwahl, spezifiziert aber auf der anderen Seite explizit die Erwartungen der Spieler (v.a. in den von der Gleichgewichtspartie unerreichten mehrelementigen Informationsbezirken). Sequenzielle Gleichgewichte sind stets teilspielperfekt, aber nicht umgekehrt. Perfekte Gleichgewichte sind immer auch sequenzielle Gleichgewichte, wobei die Umkehrung nicht immer, aber fast immer zutrifft.

Ein Gleichgewicht wird als „strikt” bezeichnet, wenn jeder unilateral abweichende Spieler relativ zu seiner Gleichgewichtsauszahlung verliert. Strikte Gleichgewichte sind immer auch perfekt und damit sequenziell (rational). Leider existieren nicht immer strikte Gleichgewichte (vgl. extensive Form, Abbildung „Extensive Form

Vertrauensspiel”), und wenn sie existieren, so können mehrere Gleichgewichte vorliegen (vgl. Normalform, Bimatrix 2 in Abbildung „Normalform”). Verfeinerte Gleichgewichtsbegriffe wie (teilspiel-)perfekte oder sequenzielle Gleichgewichte können gewisse nicht-strikte Gleichgewichte für die Lösung ausschließen. Sie können aber nicht aus einer Vielzahl von strikten Gleichgewichten lösungsgeeignete auswählen. Dies ist Aufgabe der Gleichgewichtsauswahl. Eine Theorie der Gleichgewichtsauswahl wurde zuerst von Nash (1953) für eine Klasse von Verhandlungsspielen vorgeschlagen. Die erste umfassende Theorie zur Gleichgewichtsauswahl in endlichen Spielen haben Harsanyi und Selten entwickelt. Neben generell anwendbaren Theorien wurden auch Kriterien für spezielle Klassen von Spielen vorgeschlagen, wie z.B. das intuitive Kriterium von Cho und Kreps für die (durch mehrelementige Informationsbezirke) bedingte Erwartungsbildung in dynamischen Spielen mit unvollständiger Information.

 

III. Fazit

Die Spieltheorie erlaubt es, soziale Konfliktsituationen, also strategische Spiele, facettenreich abzubilden und mathematisch streng zu lösen. Unsere einfachen Beispiele können nur andeuten, welch reichhaltiges Instrumentarium und welche teils überraschenden Einsichten die Spieltheorie hierzu offeriert. Weitere

aber nicht angesprochene

Forschungsfelder ergeben sich z.B. aus der Wiederholung eines Spiels (wiederholte Spiele) und (oder in Verbindung mit) der Berücksichtigung von unvollständiger Information. In solchen erweiterten Rahmen kann z.B. der strategische Aufbau von Reputation begründet werden. Andere Felder der Spieltheorie sind die evolutionäre Spieltheorie, die das Verhalten nicht durch rationale Entscheidungskalküle, sondern als Ergebnis von kulturellen oder genetischen Prozessen ableitet, und die so genannte kooperative Spieltheorie. Die Spieltheorie ist zuallererst eine normative Theorie. Sie wird aber auch erfolgreich bei der Erklärung von Feld- und Laborbeobachtungen sowie bei dem Design von Markt- und anderen Institutionen eingesetzt. Dennoch sollten diese Erfolge nicht darüber hinwegtäuschen, dass die deskriptive Bedeutung der Spieltheorie aufgrund der hohen Rationalitätsanforderungen ständig hinterfragt werden muss

was natürlich ebenso für die gesamte normativ ausgerichtete Wirtschaftswissenschaft zutrifft. Dies ist eine Aufgabe der experimentellen Wirtschaftsforschung, die in der Tat eine Vielzahl robuster Phänomene identifizieren konnte, die im Widerspruch zur spieltheoretischen Analyse stehen. Der verbreitete Versuch, durch leichte Abwandlungen im Optimierungskalkül der Akteure deskriptiv gehaltvolle Verhaltensprognosen zu generieren, muss angesichts der kognitiven Schranken menschlichen Handelns letztlich unbefriedigend bleiben. Daher ist parallel zur normativ ausgerichteten Spieltheorie ein aktives Forschungsfeld entstanden, dass sich vom Optimierungsprinzip abwendet und deskriptive Theorien eingeschränkt rationalen Verhaltens zu entwickeln sucht.