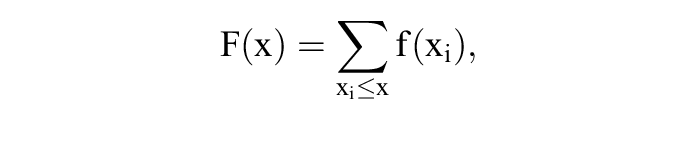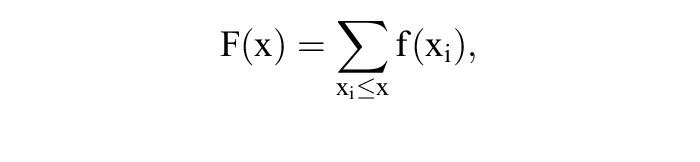Zitierfähige Version
- Revision von Verteilungsfunktion vom 16.02.2018 - 15:59
- Revision von Verteilungsfunktion vom 18.08.2017 - 16:19
- Revision von Verteilungsfunktion vom 18.01.2013 - 12:25
- Revision von Verteilungsfunktion vom 24.02.2010 - 15:54
- Revision von Verteilungsfunktion vom 28.07.2009 - 12:22
- Revision von Verteilungsfunktion vom 05.06.2009 - 15:10
Verteilungsfunktion
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
zuletzt besuchte Definitionen...
Funktion, die jeder reellen Zahl x die Wahrscheinlichkeit W(X ≤ x) = F(x) dafür zuordnet, dass die Zufallsvariable X einen Wert von höchstens x annimmt. Die Verteilungsfunktion ist eine nichtfallende Funktion, die nur Werte von 0 bis 1 annehmen kann. Bei einer diskreten Zufallsvariablen mit den Ausprägungen xi kann man die Verteilungsfunktion aus der Wahrscheinlichkeitsfunktion f(x) durch Kumulierung, also gemäß
ermitteln. Bei einer stetigen Zufallsvariablen ist die Verteilungsfunktion eine spezielle Integralfunktion der Dichtefunktion.
Bei empirischen Verteilungen wird die relative Summenfunktion gelegentlich als empirische Verteilungsfunktion bezeichnet.

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon