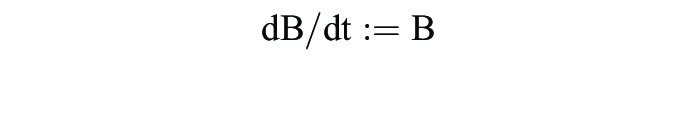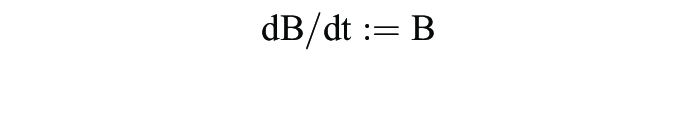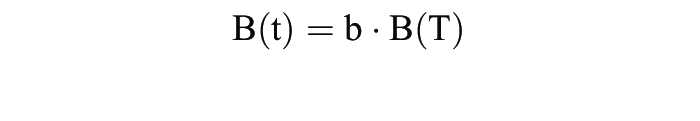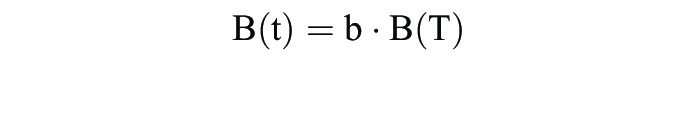exponentielles Wachstum
GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
Übersicht
zuletzt besuchte Definitionen...
Zunahme einer Größe im Zeitablauf, wenn die absolute Zunahme im Zeitablauf einem konstanten Anteil des Anfangswertes entspricht.
Beispiel: Exponentielles Bevölkerungswachstum. Wenn angenommen wird, dass die zeitliche Änderung (dt) des Bevölkerungsbestandes B
zu jedem Zeitpunkt t proportional zum gerade vorhandenen Bevölkerungsbestand B(t) ist, dann gilt für die Zunahme der Bevölkerung:
mit B(t) > 0 und einem Proportionalitätsfaktor b > 0. Nach Trennung der Variablen folgt:
dB/ B = b · dt.
Nach Integration folgt:
∫ dB/ B = b · ∫ dt + C.
Der natürliche Logarithmus (ln) dieser Funktion lautet:
ln B = b · t · C.
Die Bestandsfunktion der Bevölkerung lautet demnach:
B(t) = k · ebt,
mit der Integrationskonstanten k. Der Bevölkerungsbestand wächst exponentiell mit der stetigen Änderungsrate b (pro Zeiteinheit).
