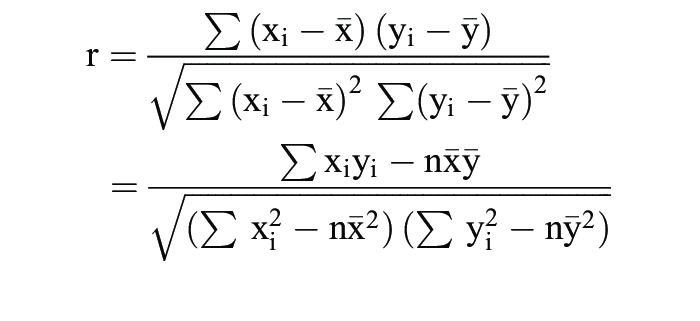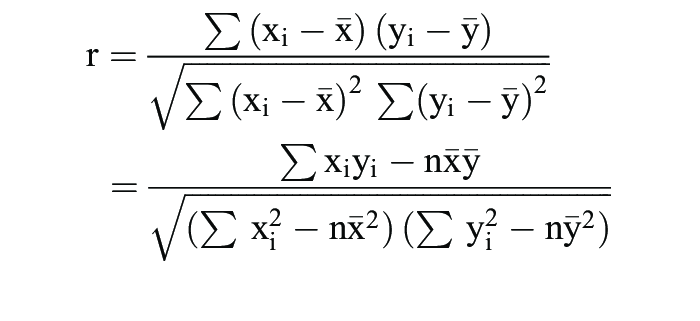Zitierfähige Version
- Revision von Korrelationskoeffizient vom 16.02.2018 - 15:59
- Revision von Korrelationskoeffizient vom 18.08.2017 - 15:16
- Revision von Korrelationskoeffizient vom 18.01.2013 - 12:25
- Revision von Korrelationskoeffizient vom 24.02.2010 - 14:42
- Revision von Korrelationskoeffizient vom 27.11.2009 - 12:30
- Revision von Korrelationskoeffizient vom 18.11.2009 - 11:02
- Revision von Korrelationskoeffizient vom 05.06.2009 - 15:05
Korrelationskoeffizient
Geprüftes Wissen

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
zuletzt besuchte Definitionen...
Korrelationsmaß; Maß, mit dem in der Korrelationsanalyse die „Stärke” eines positiven oder negativen Zusammenhangs (Korrelation) zwischen zwei quantitativen Merkmalen bzw. Zufallsvariablen gemessen werden kann. Zu beachten ist, dass der Bravais-Pearson-Korrelationskoeffizient nur den Grad des linearen Zusammenhangs misst. Ein aus einer Zufallsstichprobe berechneter Korrelationskoeffizient stellt jeweils eine Punktschätzung für den entsprechenden Koeffizienten in der Grundgesamtheit dar.
1. Bravais-Pearsonscher linearer Korrelationskoeffizient: Sind (xi,yi), i = 1, ... ,n , die n beobachteten Wertepaare des bivariaten Merkmals (X,Y), so ist der Bravais-Pearsonsche Korrelationskoeffizient durch
definiert, wobei sxy die empirische Kovarianz und sx, sy die empirischen Standardabweichungen der Merkmale X und Y in den jeweiligen Stichproben sind. Es ist also mit rxy = r
definiert, wobei und
die arithmetischen Mittel der Werte der beiden Variablen bezeichnen (Korrelationskoeffizient der Stichprobe). Dieser Korrelationskoeffizient liegt, anders als die Kovarianz sxy, immer zwischen –1 und +1. Falls die Punkte (x1,y1), ... ,(xn,yn) alle auf einer Geraden mit positiver (negativer) Steigung liegen, ist r = +1 (r = –1). Der Korrelationskoeffizient der Stichprobe hat wünschenswerte Eigenschaften als Schätzwert für den Korrelationskoeffizient der Grundgesamtheit dann, wenn letztere eine zweidimensionale Normalverteilung aufweist. Ist (X, Y) eine zweidimensionale Zufallsvariable, wobei Cov (X, Y) deren Kovarianz ist und Var X, Var Y die Varianzen der beiden Variablen bezeichnen, dann ist deren Bravais-Pearsonscher Korrelationskoeffizient
2. Spearman-Pearsonscher Rangkorrelationskoeffizient: Es seien R(xi) bzw. R(yi) der Rang des Wertes xi bzw. yi innerhalb der n Werte des ersten bzw des zweiten Merkmals, i = 1, ... ,n . Der Spearman-Pearsonsche Rangkorrelationskoeffizient rS ist der Bravais-Pearsonsche Koeffizient dieser Rangwerte und ergibt sich vereinfacht als (r=rS):
falls x1, ... ,xn und y1, ... ,yn jeweils paarweise verschieden sind. Falls die Punktepaare (x1,y1), ... ,(xn,yn) alle auf einer streng monoton steigenden (fallenden) Kurve liegen, ist rs = +1 (rs = –1). Er kann auch bei nur ordinal skalierten Merkmalen (Ordinalskala) berechnet werden. Der Wert +1 wird angenommen, wenn die Ränge in den Datenreihen x1, ... ,xn bzw. y1, ... ,yn übereinstimmen. Der Wert -1 wird angenommen, falls die Ränge ein gegenläufiges Verhalten aufweisen.

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon