Generationenmodelle
Übersicht
zuletzt besuchte Definitionen...
Neben dem Ramsey-Modell ist das OLG-Modell von Allais (1947), Samuelson (1958) und Diamond (1965) der zweite wichtige mikrobasierte Ansatz in der Makroökonomik, mit dem Ziel, die Ersparnisbildung der Haushalte und damit die Kapitalakkumulation mikroökonomisch fundiert zu erklären (s. neoklassische Wachstumstheorie). Zu jedem Zeitpunkt t sind Mitglieder unterschiedlicher Generationen am Leben, die über Märkte und/oder präferenzgesteuert (z.B. Vererbung, Bildungsausgaben für Kinder, etc.) miteinander interagieren. Ist letzteres nicht der Fall, handeln die Generationen vollkommen eigennützig, sodass sie die Auswirkungen ihrer Entscheidungen auf andere Generationen nicht berücksichtigen. Man spricht auch von Modellen sich überlappender Generationen (engl. Overlapping Generations (OLG) models). Diese Modelle bieten den Vorteil, dass Entscheidungen über den Lebenszyklus hinweg analysiert werden können (z.B. Ersparnisbildung).
1. Allgemeine Struktur des Modells: Im einfachsten Fall leben Individuen für zwei Perioden und ziehen Nutzen u aus Konsum der ersten (ct) und zweiten Lebensperiode (ct+1), sodass der Lebensnutzen U folgendermaßen formuliert werden kann
wobei ρ>0 die Zeitpräferenzrate aufgreift und zukünftiger Konsum mit der Rate β=1/(1+ρ)<1 diskontiert wird (Minderschätzung zukünftiger Bedürfnisse). Die Funktionen u(.) unterliegen den üblichen Konkavitätsannahmen, u'(.)>0 und u''(.)<0, sodass Konsum positivem aber abnehmendem Grenznutzen unterliegt. Annahmegemäß bieten Haushalte (nur) in der ersten Periode unelastisch eine Zeiteinheit Arbeit an und erzielen einen Lohn wt, welcher den Konsum heute und in der zweiten Lebensperiode finanzieren muss. Dies führt dazu, dass in der zweiten Lebensperiode nur konsumiert werden kann, wenn in der ersten Periode st gespart wird, sodass folgende Budgetrestriktion beachtet werden muss
Der Konsum der zweiten Periode entspricht dem mit dem Zins rt+1 verzinsten Konsumverzicht der ersten Periode, d.h. ct+1=(1+rt+1)st. Ouput Ytwird mithilfe einer neoklassischen Produktionstechnologie erstellt, sodass Yt=F(Kt,Lt). Lt ist der aggregierte Arbeitskräftebestand, welcher dem Arbeitsangebot der Generation entspricht, die sich gerade in ihrer ersten Lebensperiode befindet. Den Kapitalstock (Kt) der Periode t besitzt die gegenwärtig alte Generation, den sie mit ihren Ersparnissen der vergangenen Periode (t-1) aus ihrem Arbeitseinkommen angelegt hat. Die Bedingung erster Ordnung des Nutzenmaximierungsproblems liefert als optimale Beziehung zwischen gegenwärtigen und zukünftigen Konsum (sog. Euler-Gleichung):
Diese Gleichung determiniert zusammen mit der Budgerestriktion implizit die Ersparnis pro Haushalt als st=s(wt;1+rt+1). Der Kapitalstock der nächsten Periode entspricht der aggregierten Ersparnis der gegenwärtigen Periode, sodass
Damit erhält man die Kapitalintensität der nächsten Periode als
wobei Lt+1=(1+n)Lt und (1+n) den exogenen Wachstumsfaktor der Bevölkerung angibt. Unter diesen sehr allg. Annahmen sind keine geschlossenen analytischen Lösungen erhältlich. Deshalb wird in der Literatur die sogenannte kanonische Form des OLG-Modells benutzt.
2. Kanonische Form des OLG-Modells:
Damit wird die Entwicklung der Kapitalintensität unter Verwendung der Euler-Gleichung durch folgende Differenzengleichung beschrieben
Im Steady State muss gelten, dass die Kapitalintensität konstant ist, sodass
.
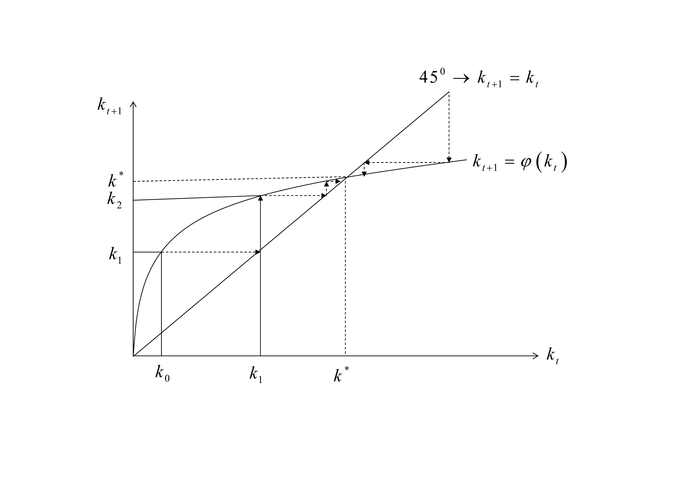
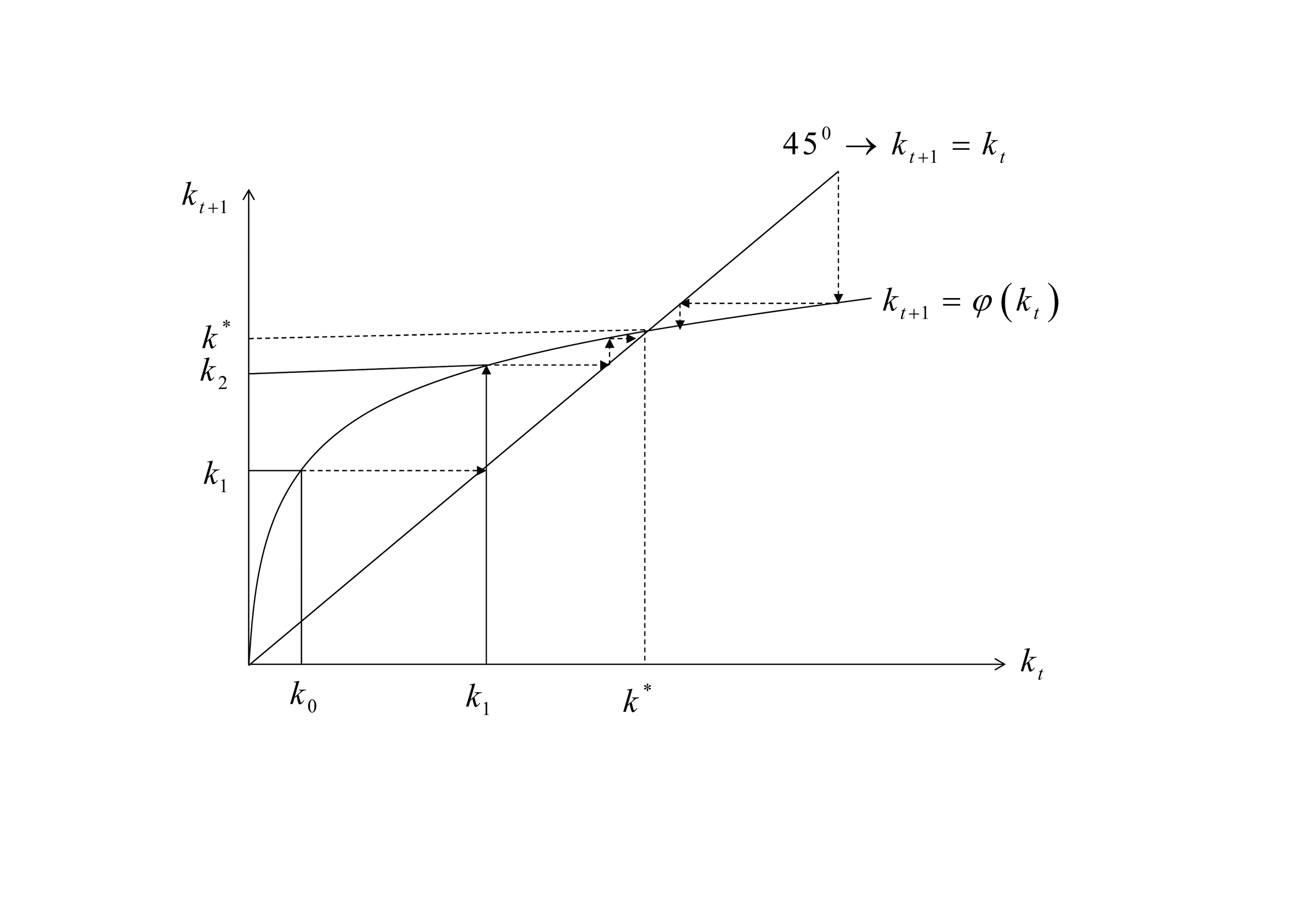
Die Anpassung an diesen Steady State veranschaulicht die folgende Abbildung, ausgehend von einem Startwert k0 in der Periode t=0.
Dieser Steady State ist global stabil, sodass Abweichungen davon Bewegungsprozesse auslösen, die zu k*zurückführen. Das resultierende Gleichgewicht stimmt im Gegensatz zum Ramsey-Modell (s. Ramsey-Modelle) nicht mit der eines sozialen Planers überein. Das Gleichgewicht kann infolge von Überakumulation nicht Pareto-optimal sein, obwohl alle Märkte kompetitiv sind. Die Ursache hierfür liegt darin, dass keine Generation bei ihrer Ersparnisbildung die Konsequenzen auf den Zins der nächsten Generation berücksichtigt. Je mehr sie also sparen, desto niedriger wird der zukünftige Zins sein, was zu noch mehr Ersparnisbildung führen kann und damit zu Überakkumulation (siehe auch goldene Regel der Kapitalakkumulation und Solow-Modell). Überakkumulation ist also das Resultat einer Externailtät durch Ersparnisbildung der gegenwärtig Jungen auf den zukünftigen Zins.
3. Altruistisches Verhalten: In einigen Anwendungen verhalten sich OLG-Haushalte nicht komplett eigennützig, sondern ziehen Nutzen aus ökonomischen Variablen ihrer Kinder, wie z.B. deren Einkommens- oder Humankapitalniveau oder aber auch deren Vermögen, was ein Vererbungsmotiv generieren würde. Verhalten sich Individuen gegenüber ihren Nachfahren vollständig altruistisch, in dem Sinne, dass das Nutzenniveveau der Nachfahren die Wohlfahrt der gegenärtigen Generation beeinflusst, würde man den Lebensnutzen folgendermaßen definieren
und sich aus Forwärtiteration folgender Zusammenhang ergeben
Obwohl jede Generation nur Nutzen aus dem Nutzenniveau ihrer direkten Nachfahren zieht, ist diese intergenerative Verknüpgfung der Haushalte hinreichend eine Planerlösung zu replizieren, in dem Sinne, als dass sich jede Generation so verhält, als ob sie die Wohlfahrt jeder jemals lebenden Generation maximieren würde. Die Lösung dieses Problems stimmt qualitativ mit dem Ramsey-Modell überein.