Solow-Modell

GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon

Übersicht

Definition Online-Lexikon (kostenlos)
Mindmap
Literaturverzeichnis/Weblinks
Sachgebiete
interne Verweise

zuletzt besuchte Definitionen...

Ausführliche Definition im Online-Lexikon

von Robert M. Solow (1956) entwickeltes Wachstumsmodell, mit dem die neoklassische Wachstumstheorie begründet wurde.

1. Struktur des Modells: Ausgangspunkt ist eine neoklassische Produktionsfunktion Y=F(K,L), wonach Output Y mit physischem Kapital K und Arbeit L produziert wird. Im Zentrum der Betrachtung steht die Entwicklung des Kapitalstocks K. Kapital wird mit einer exogenen Abschreibungsrate 0<δ<1 abgenutzt. Die Sparquote 0<s<1 und Bevölkerungswachstum n sind exogen. Ausgangspunkt des Modells ist das Gütermarktgleichgewicht einer geschlossenen Ökonomie ohne Staat zum Zeitpunkt t, sodass die aggregierte Ersparnis S_t den aggregierten Bruttoinvestitionen I_t entsprechen
   $I_t = S_t=sY_t.$
Da sich die Bruttoinvestitionen aus den Nettoinvestitionen und den Abschreibungen zusammensetzen, gilt
   $I_t = I^{net}_t + \delta K_t = S_t = s Y_t.$
Berücksichtigt man nun, dass Nettoinvestionen eine Änderung des Kapitalstocks (ΔK_t+1=K_t+1-K_t) herbeiführen, erhält man
$K_{t+1} - K_t = s Y_t - \delta K_t$
bzw. in zeitstetiger Notation
$\dot K(t) = \frac{\partial K(t)}{\partial t} = s Y(t) - \delta K(t).$
Damit steigt (sinkt) der Bestand an physischem Kapital, wenn die aggregierte Ersparnis größer (kleiner) ist als die Abschreibungen. Teilt man die letzte Gleichung durch K(t) erhält man die Wachstumsrate des Kapitalstocks

   $\frac{\dot K(t)}{K(t)} = s \frac{Y(t)}{K(t)} - \delta.$
Da die Bevölkerung, welche anahmegemäß mit dem Erwerbspersonenpotential übereinstimmt, mit konstanter Rate n wächst, zieht man sich auf die Betrachtung von Pro-Kopf-Größen, also der Entwicklung der Kapitalintensität k=K/L und des Einkommens pro Kopf y=Y/L, zurück. Weil die neoklassischen Eigenschaften für die Produktionsfunktion gelten, muss Linearhomogenität gelten, sodass für den Pro-Kopf-Output gilt:
$y = \frac{Y}{L} = F(\frac{K}{L},\frac{L}{L}) = F(k,1) =: f(k),$
wobei f als Pro-Kopf-Produktionsfunktion oder als intensive Produktionsfunktion bezeichnet wird. Offensichtlich ist das Pro-Kopf-Einkommen eine Funktion der Kapitalintensität. Steigt k steigt y. k steigt, wenn der aggregierte Maschinenbestand schneller wächst als die Bevölkerung, mathematisch:

$\frac{\dot k}{k} = \frac{\dot K}{K} - \frac{\dot L}{L}$

Damit ergibt sich für die Wachstumsrate der Kapitalintensität unter Berücksichtigung von $\dot K/K$ und $\dot L/L=n$

$\frac{\dot k}{k} &=& \frac{\dot K}{K} - \frac{\dot L}{L} = s \frac{Y}{K} - \delta - n = s \frac{Y/L}{K/L} - \delta - n\\ \frac{\dot k}{k} &=& s \frac{y}{k} - \delta - n$

bzw.

$\dot k &=& s y - (\delta + n)k.$

Dies ist die fundamentale Bewegungsgleichung des Solow-Modells.

2. Dynamik und Steady State: k steigt (sinkt), wenn

$\dot k>(<)0$ und damit auch y, wenn

$sy > (<) (\delta+n) k$ .

Bild in Originalgröße zeigen

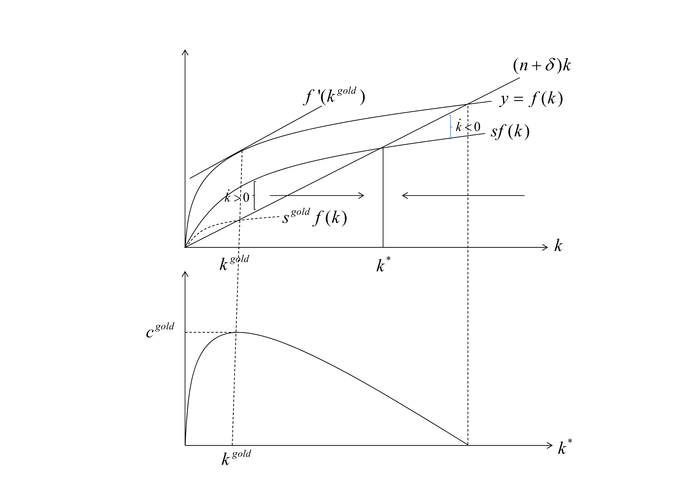
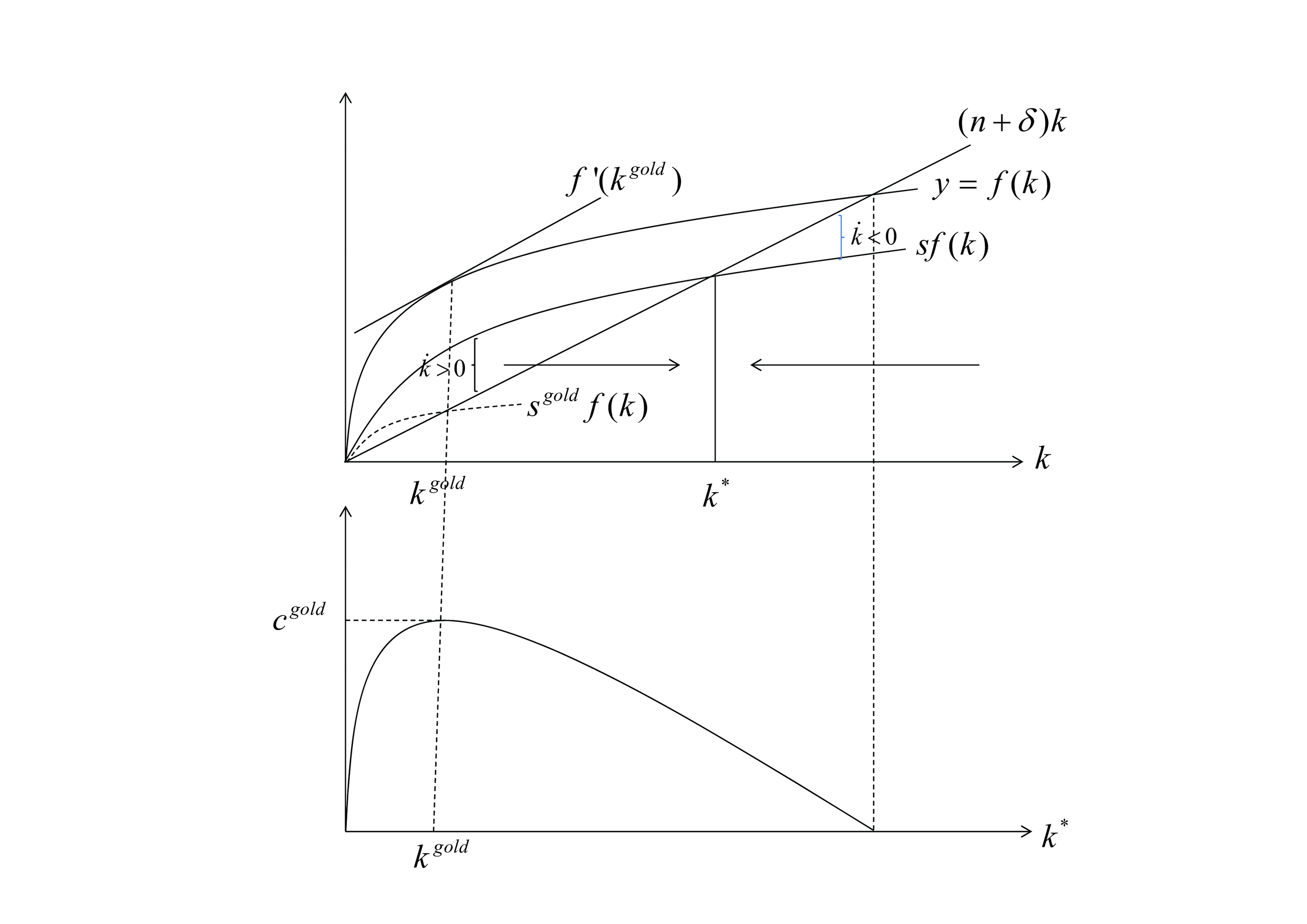
Die Kapitalintensität nimmt also zu, wenn die Pro-Kopf-Ersparnis (= Pro-Kopf-Investition) größer ist als die notwendige Investition, die erforderlich wäre, um die Kapitalausstattung pro Kopf bei Vorliegen von Abschreibungen und Bevölkerungswachstum konstant zu halten. Ist die tatsächliche Investition kleiner müssen Kapitalintensität und Output pro Kopf sinken. Ist nun dauerhaftes Wachstum in Pro-Kopf-Größen möglich? Die Antwort lautet: nein. Die Kapitalausstattung und damit der Output pro Kopf steigen solange, wie sy>(n+δ)k. Da aber y wegen positiven, aber abnehmenden Grenzerträgen konkav in k ist, muss auch sy konkav sein. Demgegenüber ist (n+δ)k eine lineare Ursprungsgerade, sodass sich beide Funktionen nur einmal schneiden können. Danach verläuft die Pro-Kopf-Ersparnis unterhalb der Ursprungsgeraden, sodass jetzt $\dot k<0$ . Im Schnittpunkt gilt sy=(δ+n)k, sodass $\dot k=\dot y = 0$ . Dies ist gleichzeitig der Steady State, ausgezeichnet durch eine konstante Kapitalintensität k^* und konstantes Prop-Popf-Einkommen y^*. Abweichungen von k^* nach rechts oder links führen wieder zum Steady State k^* zurück. Er ist damit global stabil und die Ökonomie wird dauerhaft einen Zustand mit Nullwachstum in den Pro-Kopfgrößen erreichen.

3. Mit exogenem technischen Fortschritt: Dauerhaftes Wachstum in Pro-Kopf-Größen kann nur durch Produktivitätsfortschritt erreicht werden. Das Solow-Modell behandelt diesen als exogen, d.h. er wird nicht aus dem Modell heraus erklärt. Exogener technischer Fortschritt bedeutet, dass die Arbeitsproduktivität A mit exogener Rate x wächst. Damit lautet die Produktionsfunktion jetzt Y=F(K,AL). Man spricht auch von arbeitsvermehrenden technischen Fortschritt. Die (quasi) zur Verfügung stehende Menge an Arbeit steigt also mit der Rate n und x. Deshalb ist es jetzt erforderlich, nicht mehr Pro-Kopf-Größen, sondern sogenannte Effizienzeinheiten der Arbeit zu betrachten. Der Output in Effizienzeinheiten y=Y/(AL) kann folgendermaßen beschrieben werden

    $y = \frac{Y}{AL} = F(\frac{K}{AL},\frac{AL}{AL}) = F(k,1) =: f(k),$
wobei die Kapitalausstattung in Effizienzeinheiten jetzt definiert durch k=K(AL) sich folgendermaßen entwickelt

    $\frac{\dot k}{k} &=& \frac{\dot K}{K} - \frac{\dot L}{L} - \frac{\dot A}{A} = s \frac{Y(t)}{K(t)} - \delta - n - x\\ \frac{\dot k}{k} &=& s \frac{Y(t)/AL}{K(t)/AL} - \delta - n - x\\ \frac{\dot k}{k} &=& s \frac{y}{k} - \delta - n - x$

bzw.

    $\dot k &=& s y - (\delta + n + x)k.$
Damit ist die Kapitalintensität in Effizienzeinheiten langfristig wieder konstant und genauso der Output in Effizienizeinheiten. Allerdings gilt im Steady State deshalb auch
$\frac{\dot k}{k} &=& \frac{\dot K}{K} - \frac{\dot L}{L} \frac{\dot A}{A} = 0$$

und

$\frac{\dot K}{K} - \frac{\dot L}{L} = x$ .

Damit wachsen die Kapitalintensität K/L und der Output pro Kopf Y/L im Steady State mit der Rate des technischen Fortschritts x. Das Solow-Modell ist also in der Lage langfristiges Wachstum in den Pro-Kopf-Größen zu generieren, wenn exogener technischer Fortschritt implementiert wird, aber nicht zu erklären, weil technischer Fortschritt nicht aus dem Modell heraus erklärt wird. Langfristiges Wachstum dieser Größen scheint eine empirische Regularität zu sein (siehe Kaldor-Fakten). Dementsprechend wurde das Modell kritisiert. Wie schwerwiegend diese Kritik ist, hängt vom tatsächlichen Beitrag des technischen Fortschritts zum Wirtschaftswachstum ab. Das Solow-Residuuum liegt zwischen 1/3 und 2/3. Damit kann man zumindest sagen, dass das Solow-Modell einen signifikanten Teil des Wirtschaftswachstums erklärt, aber ein signifikanter Teil bleibt unerklärt. Dieses ist Gegenstand der endogene Wachstumstheorie.

4. Die goldene Regel der Kapitalakkumulation: induziert im Wachstumsgleichgewicht eine Sparquote s^gold, welche dort den Pro-Kopf-Konsum c^* =c^gold maximiert. Konzeptionell muss im Solow-Modell der Abstand zwischen der Pro-Kopf-Produktionsfunktion y und der Ursprungsgeraden (n+δ)k maximiert werden, denn es gilt: Pro-Kopf-Konsum = Pro-Kopf-Output minus Pro-Kopf-Ersparnis. Also ist zu maximieren
$c^*=f(k^*) - (n+\delta) k^*$ ,
sodass gilt: f'(k^gold)=(n+δ). s^gold ist nun diejenige Sparquote, welche mit k^gold kompatibel ist. Ist s>s^gold so liegt dynamische Ineffizienz vor. Die Sparquote sollte reduziert werden, weil der Pro-Kopf-Konsum sofort und für alles Zeit erhöht werden kann. Ist s<s^gold, liegt dynamische Effizienz vor und die Sparquote kann nicht erhöht werden ohne gegenwärtigen Konsum zu reduzieren. Hier muss allerdings berücksichtigt werden, dass dies eine sehr technische Argumentation ist, weil diese Sparquote ein exogener Parameter ist. Im Diamond-Modell (siehe Generationenmodelle) ist die Sparquote endogenisiert. Auch diese Modelle können im Gegensatz zum Ramsey-Modell (siehe Ramsey-Modelle) Steady States hevorbringen, welche durch Kapitalüberakkumulation gekennzeichnet sein.