Bergsonsche Wohlfahrtsfunktion
GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
Übersicht
zuletzt besuchte Definitionen...
1. Begriff: Von Bergson entwickelte Wohlfahrtsfunktion. Für n Gesellschaftsmitglieder mit n individuellen Nutzenfunktionen ui lautet die gesellschaftliche Nutzenfunktion: U = f (u1, u2, ... , un).
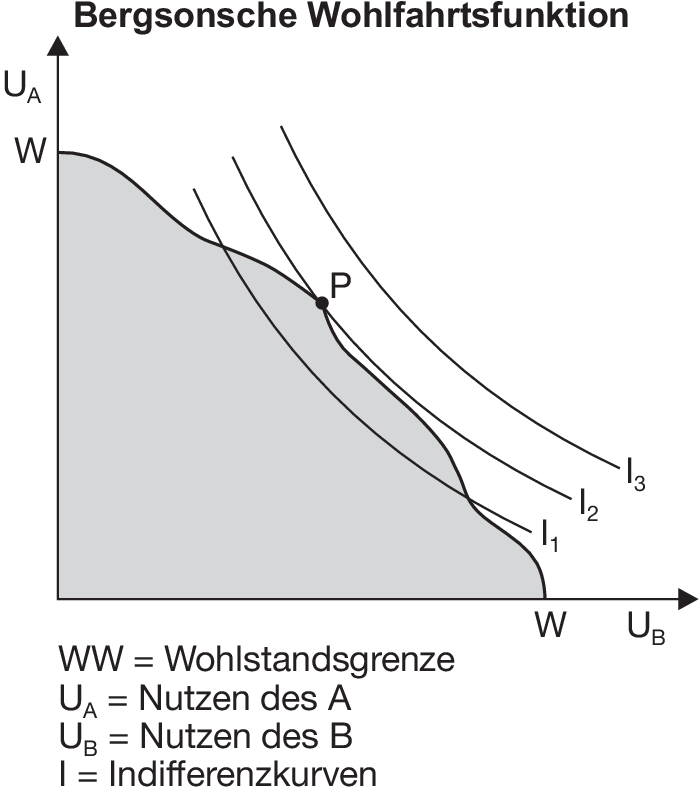
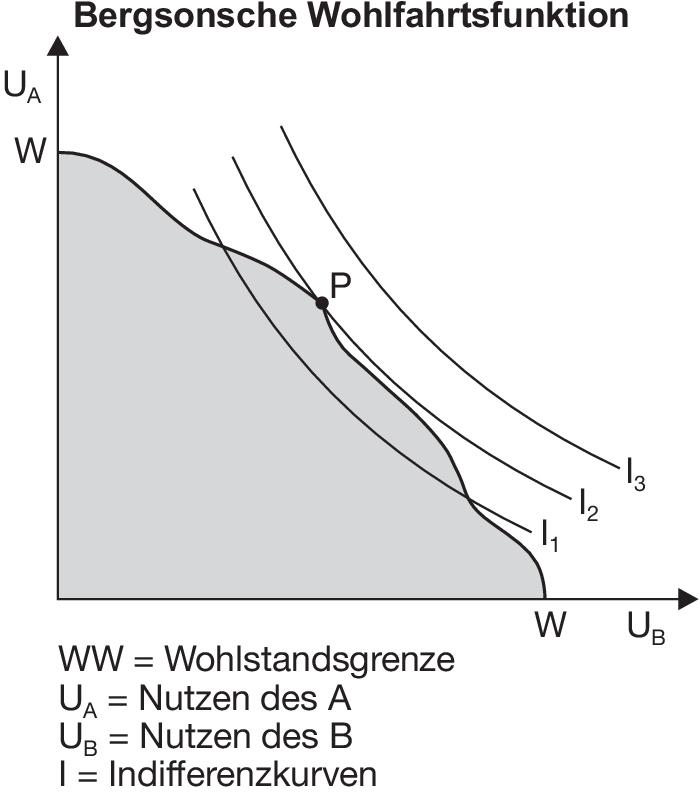
2. Herleitung: Das Wohlfahrtsmaximum wird grafisch dadurch ermittelt, dass die Nutzenfunktion U in Form eines gesamtwirtschaftlichen Indifferenzkurvensystems in das Diagramm der gesellschaftlichen Wohlstandsgrenze eingezeichnet wird (vgl. Abbildung „Bergsonsche Wohlfahrtsfunktion“). Der Tangentialpunkt P der Wohlstandsgrenze mit der Indifferenzkurve I2 der gesellschaftlichen Indifferenzkurvenschar stellt das Wohlfahrtsmaximum dar.
3. Erkenntnisziel: Mit der Bergsonschen Wohlfahrtsfunktion soll das Problem gelöst werden, dass auf der Kontraktkurve zwar ein Wohlfahrtsoptimum jedoch kein optimum optimorum definiert werden kann, da eine Bewegung entlang der Kurve unter pareto-optimalen Bedingungen nicht möglich ist.
4. Anwendungen: Ein Anwendungsbeispiel ist die im Rahmen der Allokationstheorie (Allokation) zu bestimmende Größe des öffentlichen Sektors bzw. die Entscheidung zwischen der Produktion privater und öffentlicher Güter (v.a. Samuelson und Musgrave).
