extensive Form
Übersicht
zuletzt besuchte Definitionen...
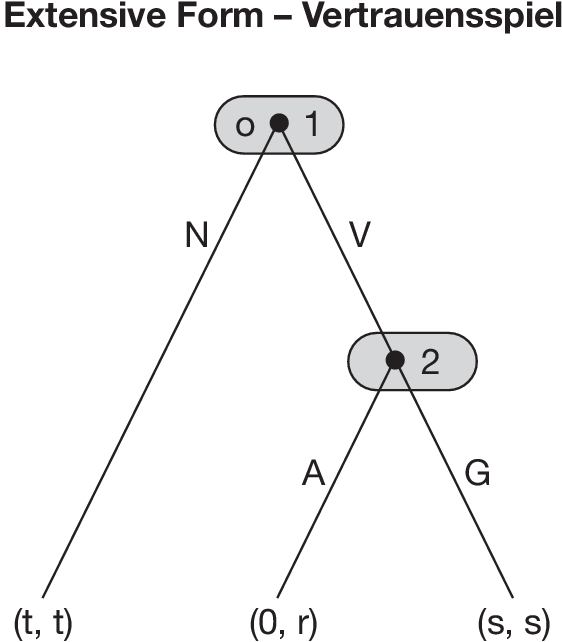
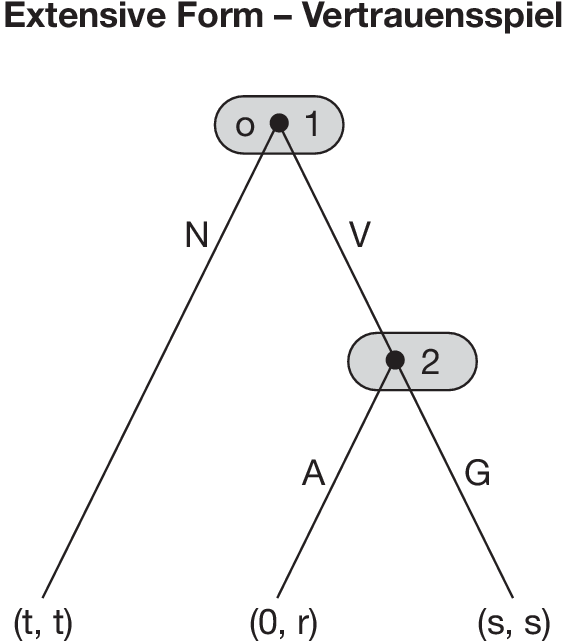
Die extensive Form eines Spiels lässt sich durch ihren komplettierten Spielbaum veranschaulichen. Dies soll am sog. Vertrauensspiel (vgl. Abbildung „Extensive Form - Vertrauensspiel”) verdeutlicht werden, dessen Parameter r, s und t die Bedingung r > s > t > 0 erfüllen.
Das Spiel beginnt im oberen Knoten o, dem Spielanfang, mit Spieler 1, der sich zwischen N (Nichtkooperation) und V (Vertrauensvoller Kooperation) entscheiden muss. Nur falls 1 den Zug V wählt, muss Spieler 2 zwischen A (Ausbeutung von 1) und G (gerechter Aufteilung) entscheiden, womit das Spiel endet. Die unteren Knoten (ohne nach unten weiterführende Äste) heißen Endpunkte bzw. Partien des Spiels. Durch die Nutzenvektoren an den Endpunkten wird in der Reihenfolge der Spieler angegeben, wie die Spieler die jeweilige Partie bewerten. Wegen s > t ziehen z.B. beide Spieler die Partie (V, G) der Partie (N) vor.
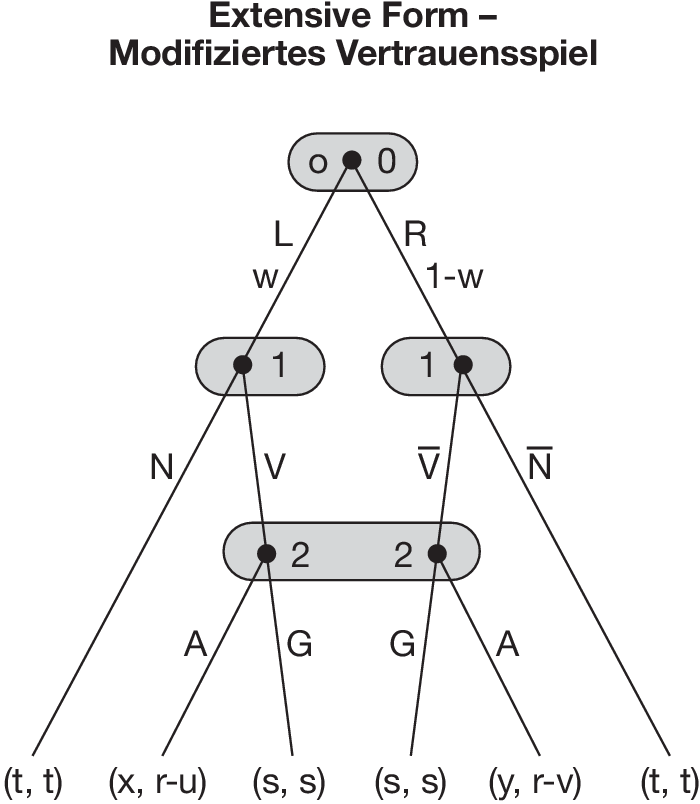
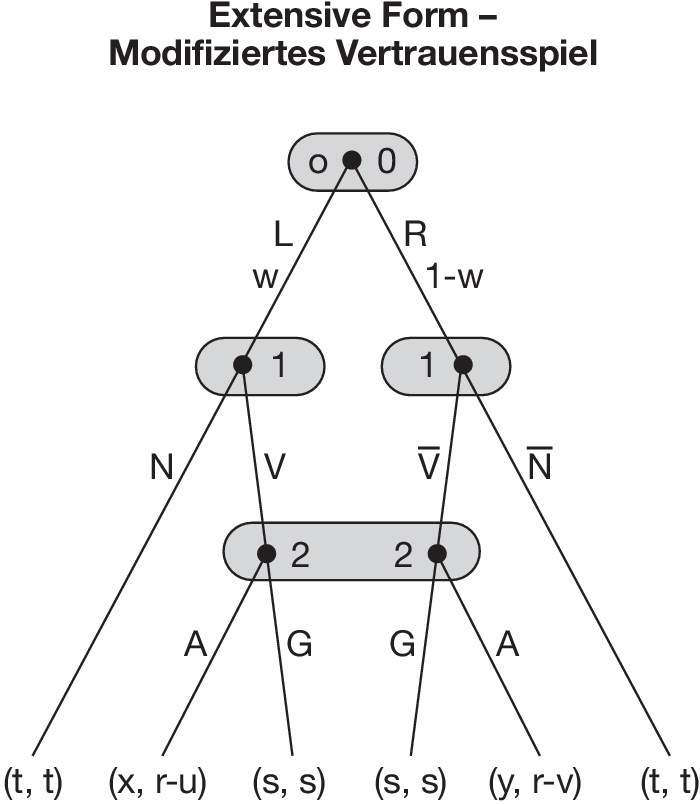
Ein Spielbaum ist ein zusammenhängender und schleifenloser Graph bestehend aus Knoten und Ästen. Für Entscheidungsknoten (mit nach unten weiterführenden Ästen) ist anzugeben, welcher Spieler (dazu zählt auch der Zufallsspieler 0 wie in Abbildung „Extensive Form - Modifiziertes Vertrauensspiel”) hier zu wählen hat. Die umkreisten Mengen heißen Informationsbezirke: Ein Spieler weiß nur, dass er sich in diesem Informationsbezirk befindet. Bei Informationsbezirken mit mehreren Knoten wie der von Spieler 2 in Abbildung „Extensive Form - Modifiziertes Vertrauensspiel” weiß er jedoch nicht, an welchem Knoten er sich befindet. Eine Entscheidung in einem Informationsbezirk muss für jeden Knoten in diesem Bezirk einen nach unten führenden Ast auswählen. Spieler 2 in Abbildung „Extensive Form - Modifiziertes Vertrauensspiel” kann also nur zwischen A und G entscheiden, da er über das Ergebnis des anfänglichen Zufallszuges nicht informiert wird.
Falls der Zufallsspieler 0 entscheidet, müssen den möglichen Ereignissen Wahrscheinlichkeiten zugewiesen werden (z.B. w für L und 1-w für R in Abbildung „Extensive Form - Modifiziertes Vertrauensspiel”). Den Endpunkten bzw. Partien sind (kardinale) Nutzenvektoren zuzuordnen, die angeben, wie die Spieler den jeweiligen Spielverlauf bewerten.
Nachteile der extensiven Form sind, dass sie nur endlich viele Zugmöglichkeiten der Spieler erlaubt und dass sie auch dann eine sequenzielle Zugfolge verlangt, wenn Spieler simultan entscheiden.
Vgl. auch Spieltheorie.