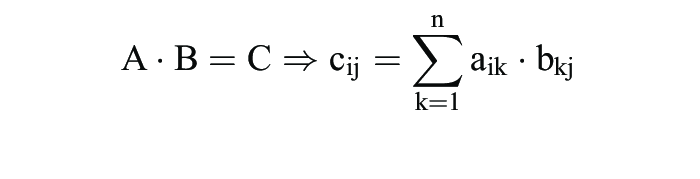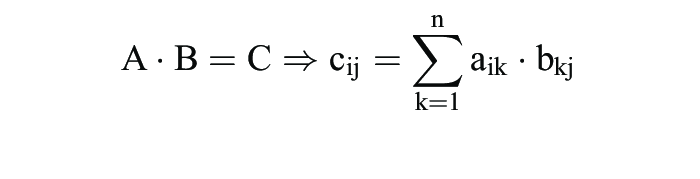Matrizenoperationen
GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
Übersicht
zuletzt besuchte Definitionen...
Folgende Matrizenoperationen werden für das Rechnen mit Matrizen (Matrix) benötigt:
(1) Gleichheit von Matrizen:
A = B, wenn alle aij = bij;
(2) Transponieren (Vertauschen von Zeilen und Spalten):
A 
AT aij aji, für alle i und j;
(3) Addition (nur bei derselben Spalten- und Zeilenzahl):
A + B aij + bij, für alle i und j;
(4) Multiplikation einer Matrix mit einem Skalar (reelle Zahl):
c · A c · aij, für alle i und j;
(5) Skalarprodukt von Vektoren (a' Zeilenvektor, b Spaltenvektor):
a'·b = a1·b1 + a2·b2 + a3·b3 + ... + an·bn ∑ R;
(6) Multiplikation von Matrizen (Spaltenzahl der ersten muss mit der Zeilenzahl der zweiten Matrix übereinstimmen):
oder cij: Skalarprodukt der i-ten Zeile von A „mal” der j-ten Spalte von B;
(7) Invertieren: Inverse.
