Teilspielperfektheit
Übersicht
zuletzt besuchte Definitionen...
Die Situation nach einigen Zügen im Verlauf eines extensiven Spiels (extensive Form) kann als eigenständiges Spiel aufgefasst werden, falls jeder Spieler vollständig über die vorangegangenen Züge informiert wurde. Derartige Substrukturen werden Teilspiele genannt. Generell beginnt in jedem Entscheidungsknoten eines Spielbaums ein Teilbaum, der alle von dort aus weiterführenden Äste und Knoten umfasst. Enthält jeder Informationsbezirk, der einen Knoten des Teilbaums umfasst, nur Knoten dieses Teilbaumes, so entspricht dem Teilbaum ein Teilspiel. D.h. Teilspiele sind informationsmäßig abgeschlossene Teilbäume.
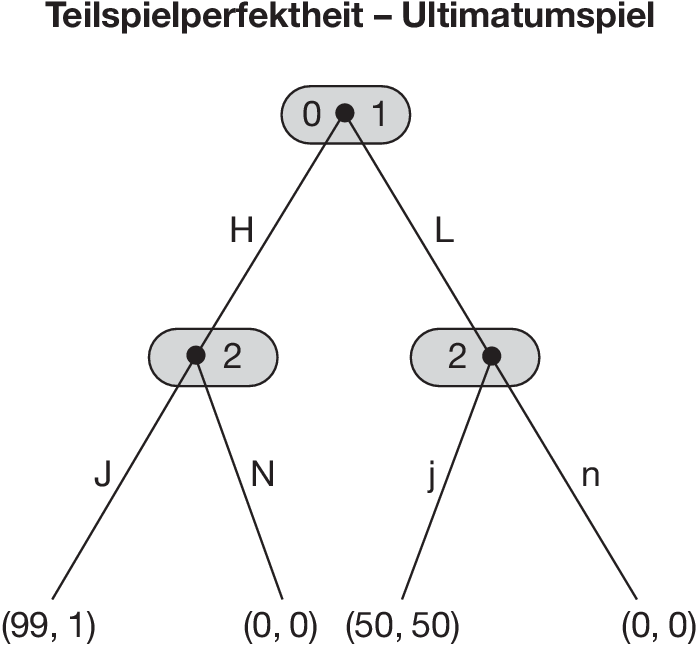
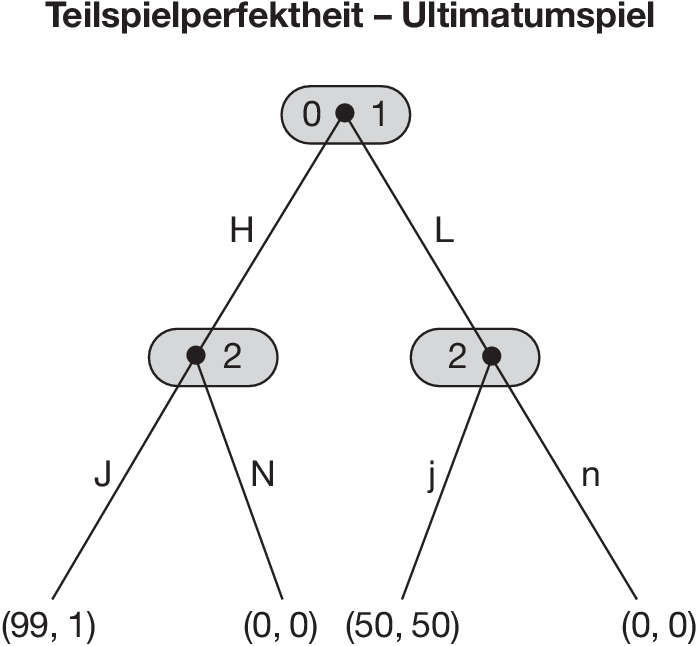
Das Ultimatumspiel der Abbildung „Teilspielperfektheit - Ultimatumspiel” verfügt über zwei echte Teilspiele, die nach dem Zug H bzw. L von Spieler 1 beginnen. Von den Gleichgewichten s1 = (H, (J, j)), s2 = (H, (J, n)) und s3 = (L, (N, j)) schreibt lediglich s1 Entscheidungen für beide Teilspiele vor, die Gleichgewichte der Teilspiele sind.
Deshalb wird häufig gefordert, nur solche Gleichgewichte s als Lösung des Gesamtspiels zu akzeptieren, deren Anweisungen für jedes Teilspiel ein Gleichgewicht des Teilspiels darstellen. Man nennt derartige Gleichgewichte teilspielperfekt. Sie erfüllen die Gleichgewichtseigenschaft nicht nur für das Gesamtspiel, sondern für alle seine Teilspiele. In der Abbildung „Teilspielperfektheit - Ultimatumspiel” ist nur die Anweisung J im Teilspiel nach H sowie j im Teilspiel nach L gleichgewichtig. Von den drei Gleichgewichten s1, s2 und s3 ist also nur s1 teilspielperfekt.
Vgl. auch Spieltheorie.