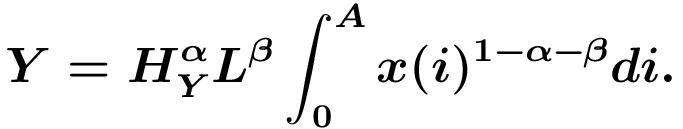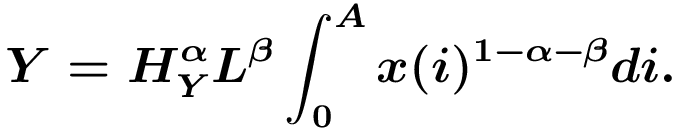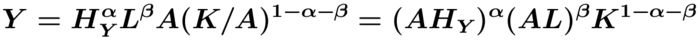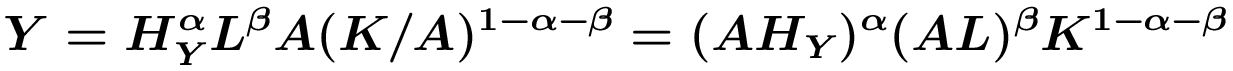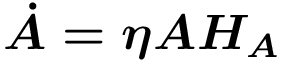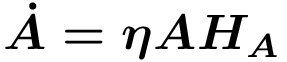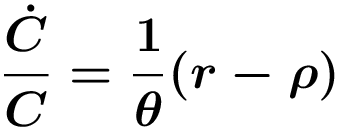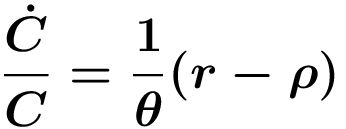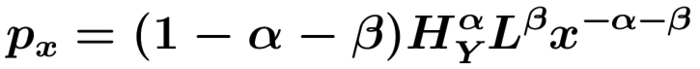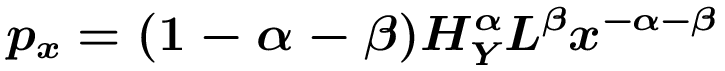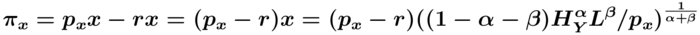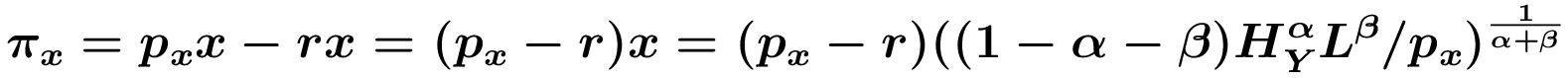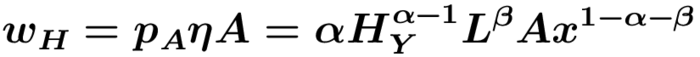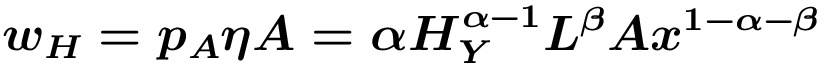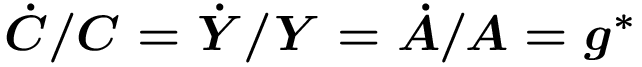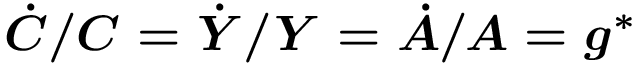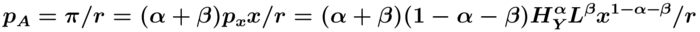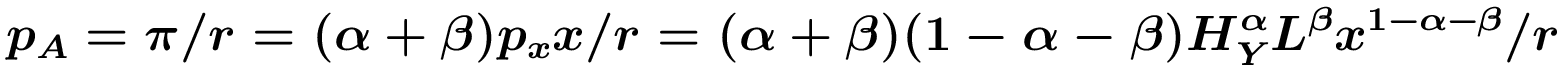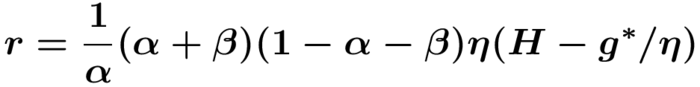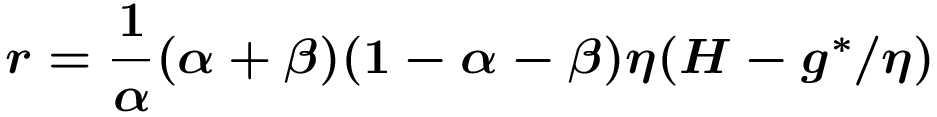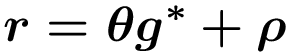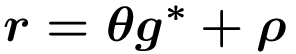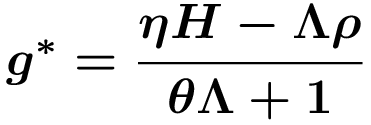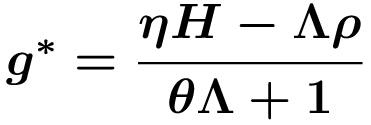Romer-Modell
GEPRÜFTES WISSEN
Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon
Übersicht
zuletzt besuchte Definitionen...
auf den Ökonomen Paul Romer (1990) zurückgehendes endogenes Wachstumsmodell. Anders als in der neoklassischen Wachstumstheorie, welche fortwährendes Wachstum des Outputs pro Kopf nur durch exogenen technischen Fortschritt generieren kann, wird dieser hier erstmals endogenisiert. Technischer Fortschritt ist das Ergebnis von gewinnorientierten Investitionen in Forschung und Entwicklung (F&E), mit dem Ziel die Variitäten von Inputs (Maschinen) zu vergrößern. Mit zunehmender "Ausdifferenzierung" des Maschinenbestandes steigt die Arbeitsteilung und damit die Produktivität der Arbeit. Da die Herstellung eines bestimmten Typs einer Maschine zunächst deren Entwicklung voraussetzt, fallen Fixkosten an, die bei vollständiger Konkurrenz nicht gedeckt werden könnten. Infolgedessen muss die Annahme der vollständigen Konkurrenz bei den Maschinenproduzenten (Zwischenproduktsektor) aufgegeben werden.
1. Struktur des Modells: Im Endproduktsektor wird ein homogenes Gut Y durch Arbeit L, Humankapital HY und einer Menge von Maschinen x(i) (= Kapital) vom Typ i, der insgesamt A(t)>0 zum Zeitpunkt t zur Verfügung stehenden Typen produziert, d.h.
Im (symmetrischen) Gleichgwicht wird von jedem Typ dieselbe Menge an Maschinen beschäftigt, sodass x(i)=x und sich der aggregierte Maschinenbestand durch K=Ax ergibt. Damit folgt für den aggregierten Output:
Durch zunehmende Spezialisierung, die sich in einem zunehmenden Maschinenbestand (Anstieg von A) ausdrückt, steigt die Arbeitsproduktivität. Durch die Produktionsfunktion von Y ergibt sich, dass alle x(i) imperfekte Substitute sind. Damit unterliegt dieser Sektor der monopolistischen Konkurrenz, was erforderlich ist, um die F&E-Auslagen der Unternehmen decken zu können. Ferner wird eine Einheit x mit einer Einheit "rohem" Kapital (nicht konsumiertem Output) hergestellt, sodass die Grenzkosten dem Zinssatz r entsprechen. F&E ist durch freien Marktzutritt und keine Unsicherheiten bzgl. des Forschungserfolgs charakterisiert. Als Input dienen Arbeit HA und alle bisher entwickelten Ideen A. Damit verändert sich A im Zeitablauf wie folgt
wobei Vollbeschäftigung HA+HY=H impliziert. Auf der Haushaltsseite wird ein unendlich lange lebender repräsentativer Haushalt bei Abwesenheit von Bevölkerungswachstum betrachtet, der den Barwert seines Nutzenstroms aus Konsum maximiert (siehe Ramsey-Modelle), mit dem Ergebnis, dass sich der Konsum optimalerweise gemäß der Keynes-Ramsey-Regel entwickelt
2. Gleichgewicht Die Nachfrage nach x-Gütern (Maschinen) im Endproduktsektor ergibt sich im Gewinnoptimum der Y-Produzenten aus der Bedingung, dass die Kosten dem Wertgrenzprodukt entsprechen müssen, wobei der Preis von Y auf 1 normiert werden kann, sodass
Da der x-Sektor der monopolistischen Konkurrenz unterliegt, muss px von den Grenzkosten r abweichen. x-Produzenten maximieren ihre Profite durch optimale Preissetzung unter Berücksichtigung der Nachfrage nach ihren Gütern
sodass ∂πx/∂pxden gewinmmaximierenden Preis px=r/(1-α-β) impliziert, mit 1/(1-α-β)>1 als "mark-up" über die Grenzkosten r. Vollständige Konkurrenz auf dem Arbeitsmarkt impliziert gleiche Löhne wH im F&E- und Endproduktsektor, sodass
Entlang des gleichgewichtigen Wachstumpfades müssen Konsum, Output und Innovationen mit gleicher und konstanter Rate g* wachsen, sodass
Damit gilt HA = g*/η. Ferner muss bei freiem Markteintritt in F&E der Preis eines Patents pA dem Barwert der Profite entsprechen, also
Berücksichtigt man ferner HY=H-HA=H-g*/η , so gilt im Lichte voranstehender Gleichung und der Beziehung für wH für den Zins einerseits
und andererseits wegen der Keynes-Ramsey-Regel
Gleichsetzen der beiden letzten Gleichungen und Auflösen nach g* liefert die Wachstumsrate der Ökonomie entlang des gleichgewichtigen Wachstumspfades
mit Λ=α/[(α+β)(1-α-β)] und g*>0, wenn ηH>Λρ.
3. Implikationen: Damit unterliegt die Wachstumsrate der Ökonomie einem Skaleneffekt, d.h. die Wachstumsrate ist positiv von der Bevölkerungsgröße abhängig (siehe bzgl. Kritik: Jones-Modell). Ferner ist die Wachstumsrate kleiner als die sozial optimale Wachstumsrate, weil F&E die Produktivität von Forschern in der Zukunft erhöht, sich diese intertemporale Externalität aber nicht in pA widerspiegelt und die Nachfrage nach Maschinen wegen der monopolistischen Verzerrung geringer ausfällt als bei vollständiger Konkurrenz. Die Lösung liegt allerdings nicht in einer Zerschlagung der Monopole, sondern in entsprechender Subvention der Verkäufe von Maschinen und Patenten.
