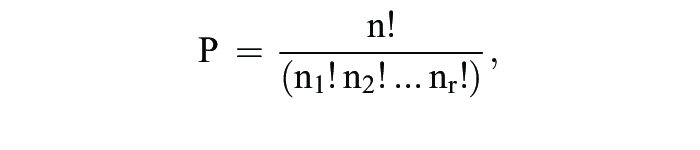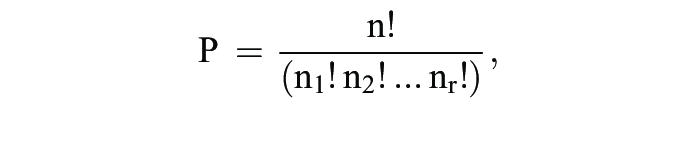Permutation
Übersicht
zuletzt besuchte Definitionen...
Ausführliche Definition im Online-Lexikon
Begriff aus der Kombinatorik. Darunter versteht man die verschiedenen Anordnungen von Elementen einer Grundmenge, wobei in jeder Anordnung alle Elemente der Grundmenge berücksichtigt werden müssen.
(1) Sind alle Elemente der Grundmenge verschieden, handelt es sich um Permutationen ohne Wiederholung:
P = n!.
(2) Lassen sich mind. zwei Elemente der Grundmenge nicht voneinander unterscheiden, handelt es sich um Permutationen mit Wiederholung. Hierbei werden die identischen Elemente der Grundmenge in r Teilmengen zusammengefasst und wird die Anzahl der Elemente aus der i-ten Teilmenge mit ni bezeichnet:
wobei: n = Anzahl der Elemente der Grundmenge, r = Teilmengen gleichartiger Elemente.
Vgl. auch Kombinatorik, Kombination, Fakultät.
Zur Zeit keine Literaturhinweise/ Weblinks der Autoren verfügbar.