Folge
(weitergeleitet von arithmetische Folge)
Übersicht
zuletzt besuchte Definitionen...
Ausführliche Definition im Online-Lexikon
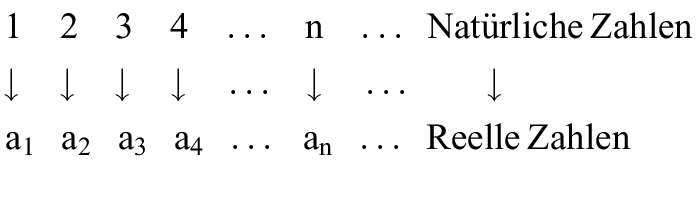
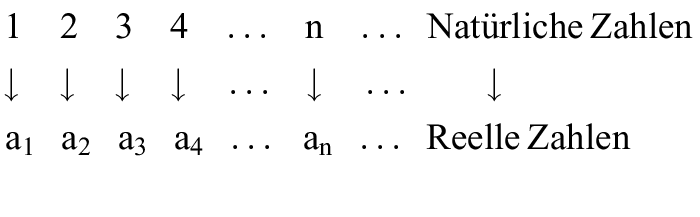
1. Begriff: Ordnet man den natürlichen Zahlen (1, 2, 3, 4, ...) durch eine beliebige Vorschrift je genau eine reelle Zahl zu, so entsteht eine Zahlenfolge. Man schreibt a1, a2, a3, ..., an, ... oder (an).
Durch die Zuordnung n → an ist eine Funktion definiert. Die an heißen Glieder der Folge.
2. Arten: a) Arithmetische Folge: Die Differenz an+1 - an = d zweier aufeinander folgender Glieder ist konstant. Das Bildungsgesetz lautet an = a1 + (n - 1) · d.
Beispiel: 10, 7, 4, 1, -2, -5, ... mit an = 10 - 3 · (n - 1).
b) Geometrische Folge: Der Quotient q = an+1/ an zwischen zwei aufeinander folgenden Gliedern ist konstant. Das Bildungsgesetz lautet:
an = a1 · qn–1.
Beispiel: 2, 4, 8, 16, ... mit an = 2 · 2n-1.
Zur Zeit keine Literaturhinweise/ Weblinks der Autoren verfügbar.