Kinky-Demand-Modell
Übersicht
zuletzt besuchte Definitionen...
1. Begriff: Oligopolmodell (Oligopol) der einfach geknickten Preisabsatzkurve (im Unterschied zur doppelt geknickten Preisabsatzkurve - vgl. Preisabsatzfunktion, monopolistische Konkurrenz), das die Preisstarrheit im Oligopol erklären soll.
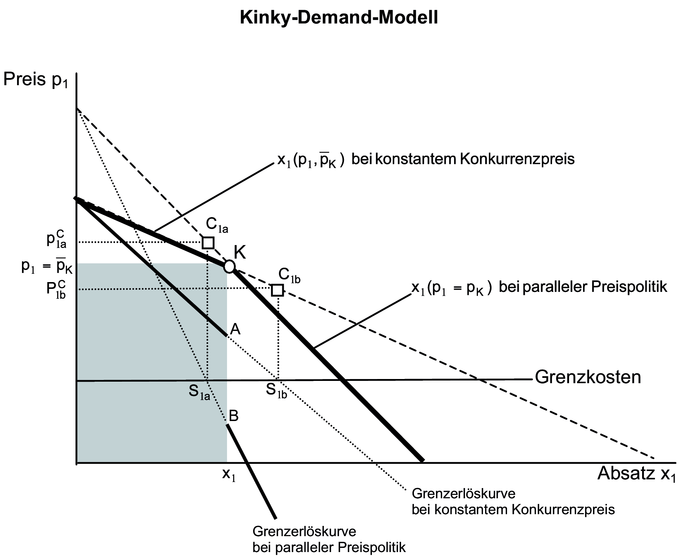
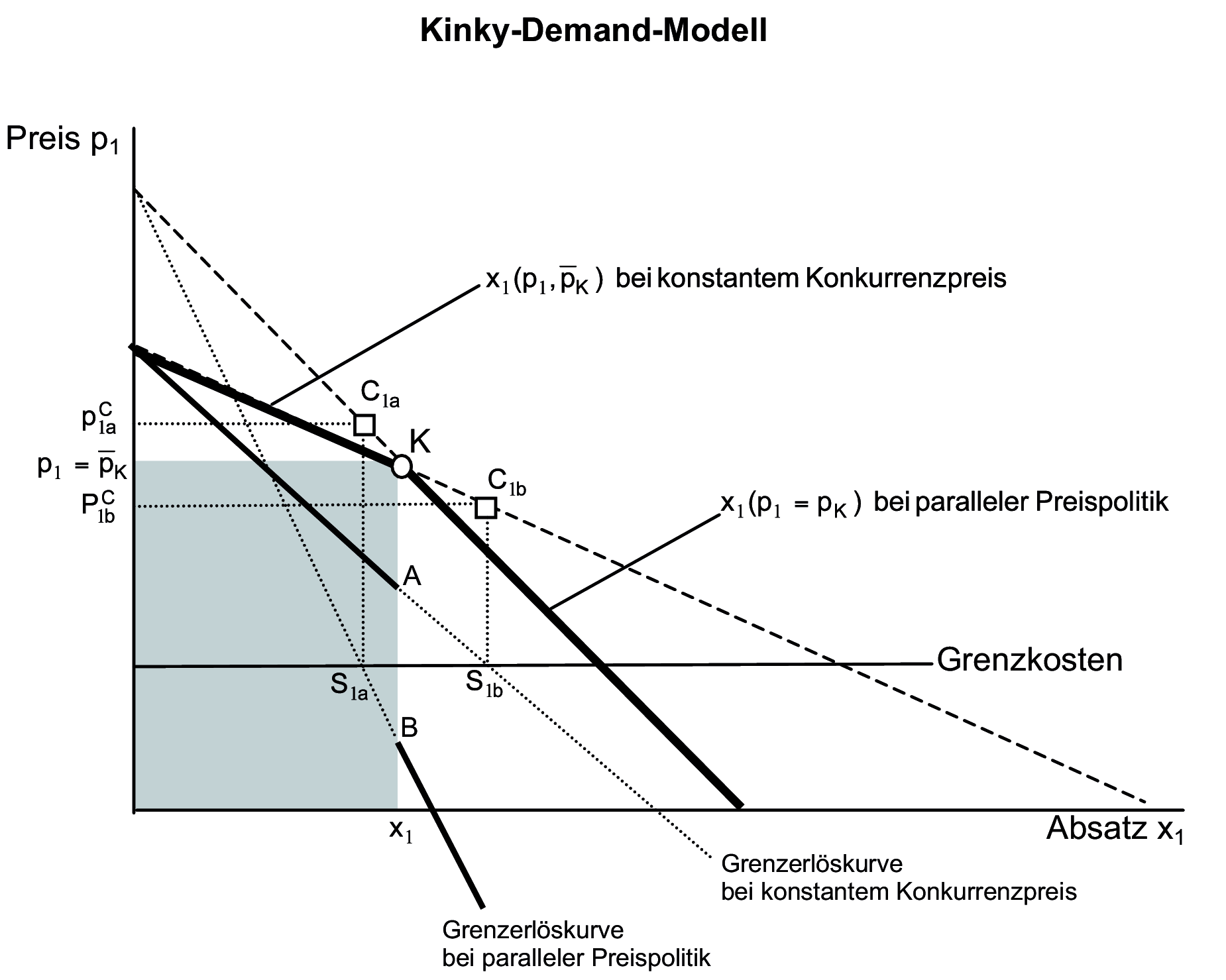
2. Begründung der Kinky-Dermand-Curve: Der Knick in „der” Preisabsatzkurve (vgl. Abb. Kinky-Demand-Modell) kommt dadurch zustande, dass bei Annahme heterogener Konkurrenz zwei verschiedene oligopolistische Preisabsatzfunktionen mit asymmetrischer Erwartung über das Konkurrenzverhalten kombiniert werden. Der betrachtete Anbieter 1 befindet sich in der Ausgangslage, die durch einen gleich hohen Konkurrenzpreis (p1= pK) chrakterisiert ist, in der Preis-Mengen-Kombination K(p1,x1).
a) Im Falle einer Preissenkung erwartet er, dass die Konkurrenz mitziehen wird, weil diese sonst je nach Preisunterbietung mehr oder weniger Absatz und Gewinn verlieren würde. Es gilt dann die Preisabsatzfunktion bei weiterhin gleich hohen Konkurrenzpreisen, mit anderen Worten die Preisabsatzfunktion bei „paralleler” Preispolitik:
.
b) Im Falle einer Preiserhöhung erwartet er umgekhrt, dass die Konkurrenz nicht mitziehen, sondern ihren Preis konstant halten wird, weil sie dann von seinen Absatzverlusten profitieren könnte. Es gilt in diesem Fall die Preisabsatzfunktion bei konstantem Konkurrenzpreis:
,
Da die Preisabsatzkurve bei paralleler Preispolitik wegen des ausbleibenden Käuferwechsels steiler verläuft als bei konstantem Konkurrenzpreis (auf letzterer verliert er im Alleingang bei Preiserhöhungen Käufer an die Konkurrenz, während er bei einer alleinigen Preissenkung von der Konkurrenz Käufer gewinnt) entsteht beim Ausgangspreis der besagte Knick.
3. Begründung der Preisstarrheit: Unterstellt man für den betrachteten Oligopolisten Gewinnmaximierung als Zielsetzung, wird an der Lage der Cournot-Punkte auf beiden (durchgängig betrachteten) Preisabsatzkurven sein ganzes Gewinndilemma deutlich. Bei paralleler Preispolitik liegt der gewinnmaximale Cournot-Punkt C1a- unerreichbar! - oberhalb von K auf der gestrichelten Weiterführung des unteren Astes der -geknickten Preisabsatzkurve. Bei konstantem Konkurrenzpreis im gewinnmaximalen Punkt C1b - ebenfalls unerreichbar! - unterhalb von K auf der gestrichelten Fortführung der Preisabsatzkurve bei konstantem Konkurrenzpreis. Quintessenz: Bei einer alleinigen Preiserhöhung würde er sich von C1b entfernen und bei einer parallelen Preissenkung von C1a, sodass er bei einer Preisveränderung in jedem Fall Gewinn einbüßen würde. Also kann er als second-best-Lösung nur den bisherigen Preis beibehalten. Dass es sich im erzwungenen Knickpunkt nicht um eine echtes Gewinnmaximum handelt, wird daran erkennbar, dass zwischen der (horizontalen) Grenzkostkurve und der zu der gekickten Preisabsatzkurve gehörenden Grenzerlöskurve kein Schnittpunkt existiert. Denn die Grenzkostenkurve verläuft senkrecht unterhalb von K zwischen A und B durch eine Sprungstelle. Infolgedessen kann die Gewinnmaximierunsbedingung (Grenzerlös = Grenzkosten) nicht erfüllt werden.
4. Kritik: Damit relativiert sich aber auch das Argument der Preisstarrheit: a) Schneiden die Grenzkosten die Grenzerlöskurve oberhalb von A, ergibt sich ein gewinnmaximierender Preiserhöhungsspielraum auch im Alleingang.
b) Schneiden die Grenzkosten die Grenzerlöskurve unterhalb von B eröffnet sich ein gewinnmaximierender Preissenkungsspielraum, selbst wenn die Konkurrenz mitzieht.
Auch wenn diese Alternativfälle nicht relevant werden, bleibt die Annahme fragwürdig, dass sich die Konkurrenz bei ihrer Preisentscheidung nur an den resultierenden Absatzgewinnen oder -verlusten orientiert. Unterstellt man auch für die Konkurrenz gewinnmaximierendes Verhalten, ergibt sich ein Desinteresse an einer Preisaktion oder -reaktion erst im Bertrand-Gleichgewicht.
Vgl. oligopolistische Preisbildung.