Bilanzgerade
Übersicht
zuletzt besuchte Definitionen...
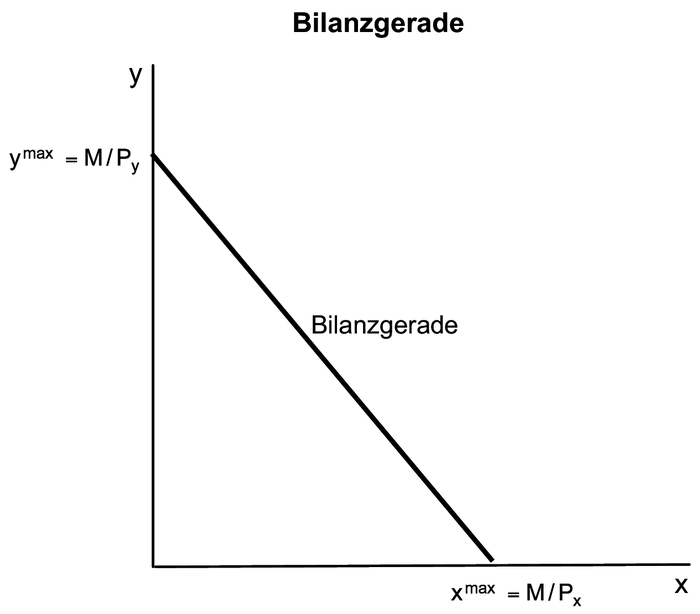
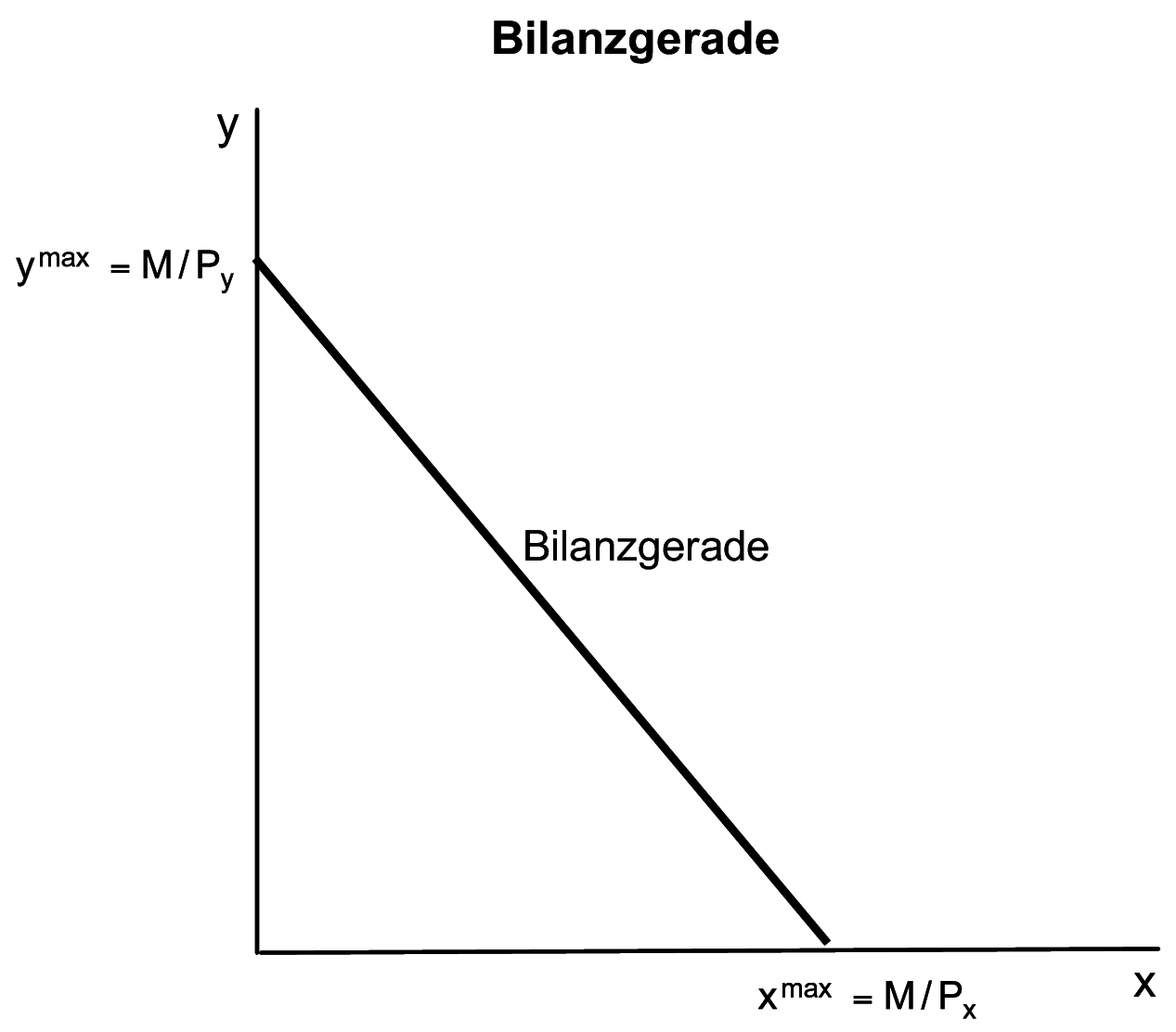
Budgetgerade, Haushaltsgerade; Begriff aus der Nachfragetheorie des Haushalts; gibt im Zwei-Güter-Modell den Zusammenhang zwischen dem geplanten Budget M, d.h. den für Konsumausgaben vorgesehenen Teil des Einkommens eines Haushalts, und den damit bei voller Ausschöpfung des Budgets realisierbaren Gütermengen x und y bei gegebenen Güterpreisen Px und Py wieder. Sie folgt aus der Budgetrestriktion xPx + yPy ≤ M, welche besagt, dass die Summe aller mit ihren Preisen multiplizierten Konsumgütermengen nicht größer sein darf als die budgetierte Ausgabensumme des Haushalts. Wird das zur Verfügung stehende Bugdget genau verausgabt, lässt sich aus der Budgetgleichung xPx + yPy = M durch Auflösung nach y die Funktion y(x) der Bilanzgeraden in der Mengenebene ermitteln:
Während die Steigung der Bilanzgeraden dy/dx=-Px/Py durch das negative Verhältnis der Güterpreise bestimmt wird, ergibt sich der Achsenabschnitt auf der y-Achse, d.h. der maximale y-Konsum bei Nichtkonsum des Gutes X (x = 0), durch ymax = M/Py.
Umgekehrt wird der Achsenabschnitt auf der x-Achse, also der maxmimale x-Konsum bei Nichtkonsum des Gutes Y (y = 0), durch xmax = M/Px bestimmt.
Bei der Ermittlung der optimalen (d.h. nutzenmaximalen) Konsumgütermengenkombination bildet die Bilanzgerade (vgl. Abbildung "Bilanzgerade") die rechte Grenze des Lösungsraumes für das Haushaltsgleichgewicht.