Angebotstheorie des Haushalts

1. Begriff: Im Rahmen der Haushaltstheorie die Theorie des Einkommenserwerbs durch das Faktorangebot des privaten Haushalts: Indem er Arbeitsleistungen anbietet, ist der Haushalt einerseits in der Lage, jenes Einkommen zu erzielen, welches Voraussetzung für die Entfaltung seiner Nachfrage nach Konsumgütern ist. Andererseits ist das Arbeitsangebot auch ein Beitrag zu jener Faktorausstattung, welche die Produktion der nachgefragten Endprodukte erst ermöglicht. Damit wird auch die Einbindung des Haushalts in den volkswirtschaftlichen Kreislauf sowie die Interdependenz von Angebots- und Nachfragetheorie des Haushalts deutlich.

2. Determinanten: Die Höhe des individuellen Arbeitsangebotes in der Planperiode (z.B. für einen Tag) hängt erstens von der Entscheidung des Haushalts über die Aufteilung der ihm max. zur Verfügung stehenden Zeit h^max (theoretisch 24 Stunden pro Tag) auf Arbeitszeit h_A und Freizeit h_F ab, sowie zweitens von der Realeinkommenserzielung y durch die Leistung von Arbeitsstunden zu einem gegebenen Reallohnsatz (W/P) pro Stunde (mit dem nominellem Stundenlohn W und dem Konsumgüterpreisniveau P). Beide Argumente - der mit dem realen Arbeitseinkommen erreichbare Güternutzen und der Freizeitnutzen - bestimmen gemeinsam die Nutzenposition U des Haushalts (U = U(y,h_F). Denn das nomininelle Einkommen ist durch seinen Einfluss auf das Haushaltsbudget (und damit auf die Budget- bzw. Bilanzgerade) die Grundlage für die Aufstellung des optimalen Konsumplans und bei gegebenem Konsumgüterpreisniveau auch für die Erzielung von Nutzen aus Konsumgütern. Mit der Zeitaufteilung wird gleichzeitig auch die Höhe des Freizeitnutzens bestimmt, der aus dem Genuss von Freizeit resultiert. Enthalten ist hier die Annahme, dass Arbeit keinen direkten Nutzen stiftet, sondern als „Arbeitsleid” zu charakterisieren ist.

Bild in Originalgröße zeigen

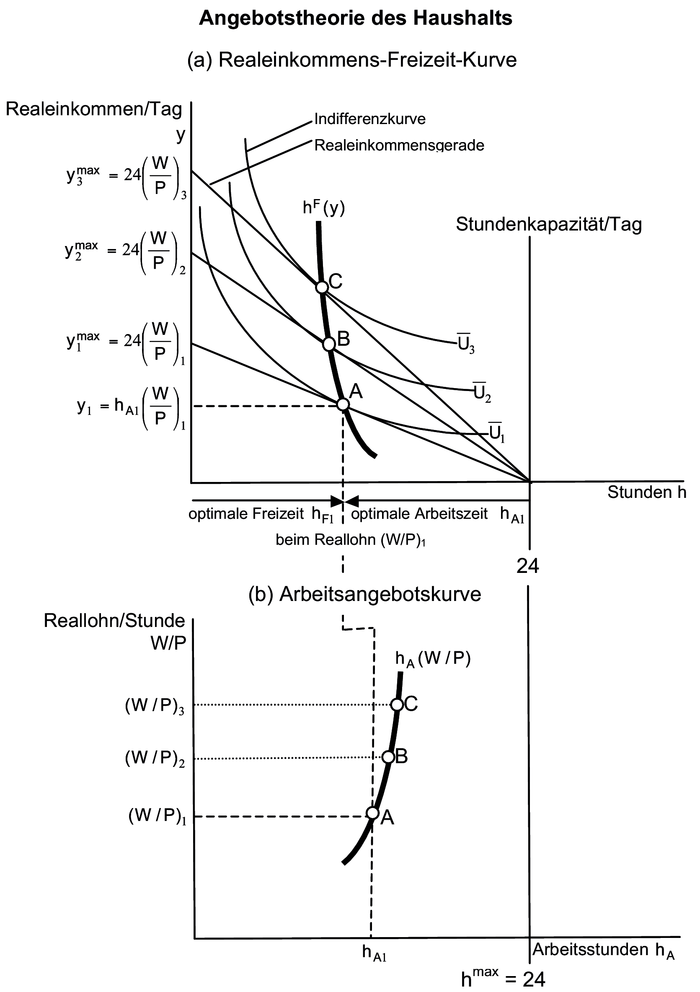
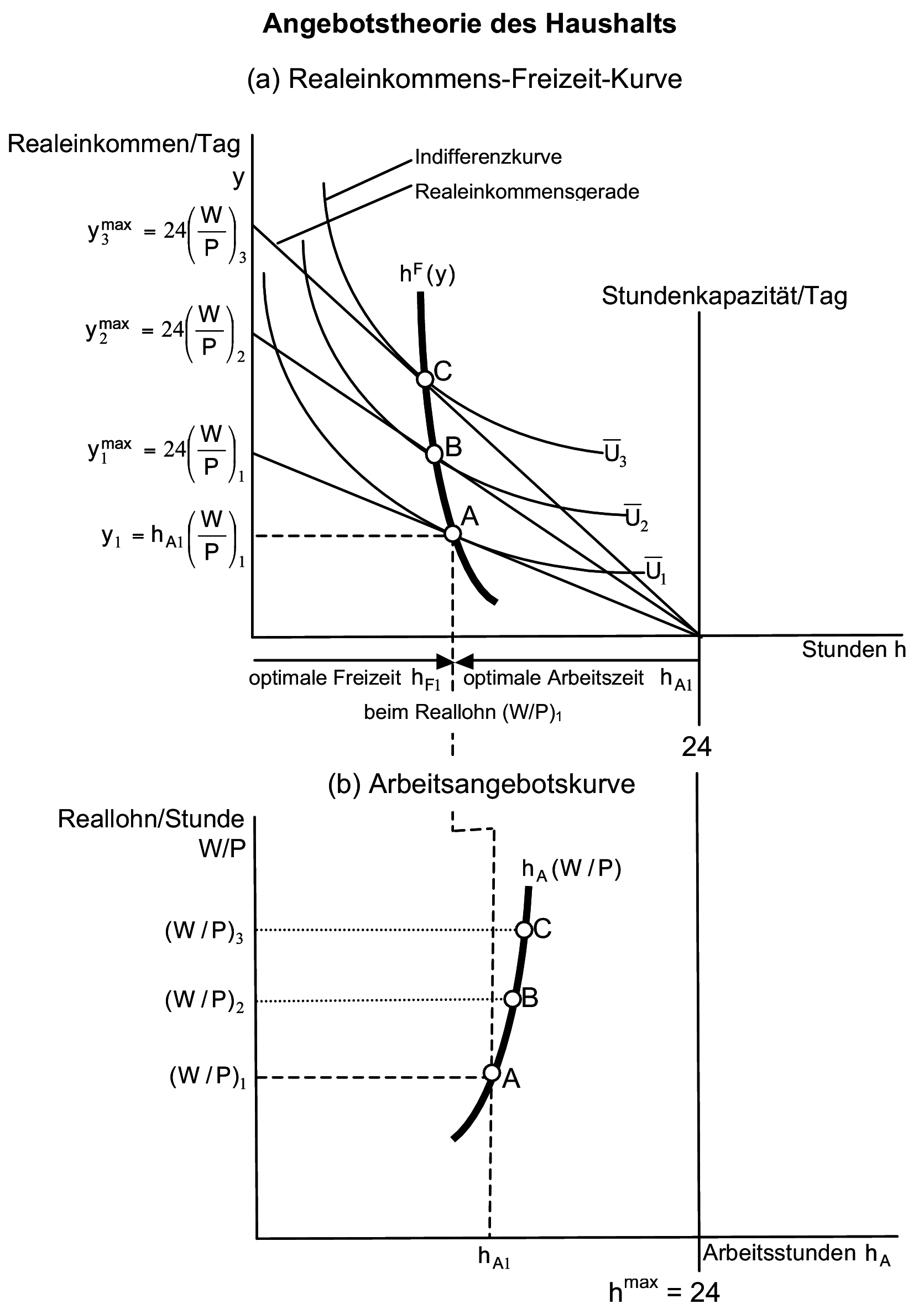
3. Grafische Darstellung: Die zu einem bestimmten Reallohn pro Stunde in Abhängigkeit von der Arbeitszeit erzielbaren Realeinkommen (y =(W/P)h_A) können in Form der Realeinkommensgeraden grafisch erfasst werden (vgl. Abb. (a) Realeinkommens-Freizeit-Kurve), deren Steigung durch den jeweiligen realen Stundenlohn (W/P) bestimmt wird. Das max. Realeinkommen/Tag y^max =24(W/P) wird (als Abschnitt jeder Realeinkommensgeraden auf der y-Achse ablesbar) erzielt, wenn ohne Freizeit „rund um die Uhr” gearbeitet würde. Die Präferenzordnung des Haushalts bez. Realeinkommen (=Konsumgüternutzen) und Freizeitnutzen wird durch die Schar hyperbelförmiger Indifferenzkurven mit nach rechts oben ansteigendem Nutzenindex abgebildet. Die optimale, d.h. nutzenmaximale Aufteilung des Zeitbudgets auf Arbeits- und Freizeit ergibt sich für jeden realen Stundenlohn dort, wo die zugehörige Realeinkommensgerade eine Indifferenzkurve tangiert, nämlich diejenige Indifferenzkurve mit dem höchsten erreichbaren Nutzenindex. Bspw. ergibt sich beim Reallohn (W/P)₁ der Tangentialpunkt A mit der optimalen Freizeit h_F1 und der optimalen Arbeitszeit h_A1 sowie dem realen Arbeitseinkommen y₁. Aus den Tangentialpunkten verschiedener Realeinkommensgeraden kann weiter die Realeinkommens- oder Lohn-Freizeit-Kurve ermittelt werden, aus der - unter der Annahme, der Haushalt könne sein Arbeitsangebot frei wählen - schließlich die Arbeitsangebotskurve ableitbar ist (vgl. Abb. (b) Arbeitsangebotskurve). Sie stellt den funktionalen Zusammenhang zwischen dem Reallohnsatz/Stunde (W/P) und dem Arbeitsangebot h_A dar. Ihr konkreter Verlauf beruht auf der Lage und Gestalt der Indifferenzkurven, d.h. der angenommenen Nutzenfunktion. Im Normalfall ist der Verlauf der Arbeitsangebotskurve umgekehrt s-förmig, d.h. für sehr niedrige Lohnniveaus invers, sodass bei fallendem Lohnsatz das Arbeitsangebot gesteigert werden muss, um das Existenzminimum zu sichern. Dabei können Veränderungen der Höhe des Arbeitsangebots mithilfe des Einkommenseffekts und des Substitutionseffektes betrachtet werden. Im Normalbereich (wie in der Abb. (b) nur dargestellt) wird aufgrund der zunehmenden Opportunitätskosten der Freizeit das Arbeitsangebot mit dem Reallohnsatz steigen, während es für höhere Lohnniveaus, bei denen der Nutzen der Freizeit höher als das zusätzlich erzielbare Realeinkommen bewertet wird, fällt.

4. Analytischer Lösungsansatz: Mathematisch lässt sich die Optimalbedingung der Tangentenlösung mithilfe der Lagrangemethode ermitteln. Für das Nutzenmaximierungsproblem des Haushalts hinsichtlich der Arbeitsangebotentscheidung gilt die Zielfunktion U=U(y,h_F)=max mit der Nebenbedingung yP-W(24-h_F)=0. Aus der entsprechenden Langrangefunktion L=U(y,h_F)-λ(yP-W(24-h_F)) folgt die Optimalbedingung:

In Worten: Im Optimum (Tangentialpunkt) muss die Grenzrate der Substitution zwischen Freizeit und Realeinkommen aus Arbeitszeit (d.h. die Steigung der Indifferenzkurve) dem Reallohn (der Steigung der Realeinkommensgeraden) entsprechen.