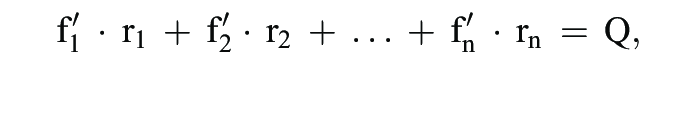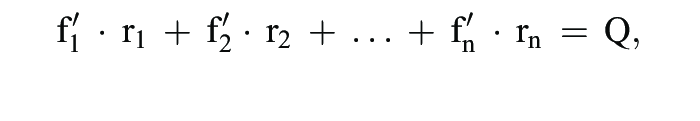SUCHE
1234
Suchformular schließen

Eulersches Theorem

GEPRÜFTES WISSEN
 Über 200 Experten aus Wissenschaft und Praxis.
Mehr als 25.000 Stichwörter kostenlos Online.
Das Original: Gabler Wirtschaftslexikon

Übersicht

zuletzt besuchte Definitionen...

    Ausführliche Definition im Online-Lexikon

    Euler-Theorem, Ausschöpfungstheorem, Adding-up-Theorem. Bei linear-homogenen Produktionsfunktionen (vgl. auch Linearhomogenität) gilt:

    wobei: f'i = partielle Grenzproduktivität des Faktors i, ri = gesamte Einsatzmenge des Faktors i, Q = Output.

    Bei vollständiger Konkurrenz ist das Wertgrenzprodukt p · f'i als Produkt aus Güterpreis p und partieller Grenzproduktivität gleich dem Faktorpreis qi. Multiplikation der obigen Relation mit dem Produktpreis P ergibt daher:

    q1 r1 + q2 r2 + ... + qn rn = Q · P.

    Die Summe der Kosten für die Produktionsfaktoren zehrt den gesamten Erlös auf, es bleibt kein Gewinn.

    Vgl. auch Wicksell-Cobb-Douglas-Produktionsfunktion.

    Übersicht

    zuletzt besuchte Definitionen...

      Mit Ihrer Auswahl die Relevanz der Werbung verbessern und dadurch dieses kostenfreie Angebot refinanzieren: Weitere Informationen

      Mindmap "Eulersches Theorem"

      Hilfe zu diesem Feature
      Mindmap Eulersches Theorem Quelle: https://wirtschaftslexikon.gabler.de/definition/eulersches-theorem-33283 node33283 Eulersches Theorem node45598 Produktionsfaktoren node33283->node45598 node42560 Produktionsfunktion node33283->node42560 node34046 Grenzproduktivität node33283->node34046 node31465 Arbeit node45598->node31465 node38061 Kapital node45598->node38061 node42560->node45598 node42560->node31465 node42560->node38061 node34046->node45598 node34046->node42560 node32438 Grenzproduktivitätstheorie node32438->node33283 node32438->node45598 node34979 Ertragsgesetz node32438->node34979 node36260 Homogenität node36260->node33283 node36260->node45598 node36260->node42560 node42118 Nutzentheorie node36260->node42118 node36260->node34979 node50317 technischer Fortschritt node50317->node32438 node46151 Produktivität node46151->node34046 node31119 Arbeitsmarkttheorien node31119->node34046 node36167 Economies of Scale node36167->node42560 node48087 Unternehmen node48087->node45598 node41897 Kennzahlen node41897->node45598 node31465->node32438
      Mindmap Eulersches Theorem Quelle: https://wirtschaftslexikon.gabler.de/definition/eulersches-theorem-33283 node33283 Eulersches Theorem node45598 Produktionsfaktoren node33283->node45598 node42560 Produktionsfunktion node33283->node42560 node34046 Grenzproduktivität node33283->node34046 node32438 Grenzproduktivitätstheorie node32438->node33283 node36260 Homogenität node36260->node33283

      News SpringerProfessional.de

      Autoren der Definition und Ihre Literaturhinweise/ Weblinks

      Zur Zeit keine Literaturhinweise/ Weblinks der Autoren verfügbar.

      Literaturhinweise SpringerProfessional.de

      Bücher auf springer.com

      Sachgebiete

      Eulersches Theorem

      is assigned to the following subject groups in the lexicon:

      BWL

      Allgemeine BWL > Produktion > Produktions- und Kostentheorie

      VWL

      Wirtschaftstheorie > Mikroökonomie > Preis- und Markttheorie

      Weiterführende Schwerpunktbeiträge

      Produktionsplanung und -steuerung

      Die Produktionsplanung und -steuerung (PPS) als Teilbereich des operativen Produktionsmanagements hat für die wirtschaftliche Gestaltung und den reibungslosen Ablauf der Produktionsprozesse zu sorgen. Dieser Beitrag beschreibt die im Rahmen der Produktionsplanung und -steuerung durchzuführenden Planungsschritte.... mehr >

      Interne Verweise