Neukeynesianische Makroökonomik, statisches Zwei-Länder-Modell
Übersicht
zuletzt besuchte Definitionen...
1. Charakterisierung: Das statische neukeynesianische Modell für die kleine offene Volkswirtschaft (Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell) lässt sich zu einem analogen Modell für große offene Volkswirtschaften erweitern, indem dieses zu einem Zwei-Länder-Modell ausgebaut wird. Das neukeynesianische Zwei-Länder-Modell besteht aus zwei realzins- und relativpreisabhängigen IS-Gleichungen, der Bedingung für die ungedeckte Zinsparität, zwei Zinsregeln und zwei Inflationsgleichungen vom Philips-Kurven-Typ. Wird von zwei strukturell vollkommen symmetrischen Ländern ausgegangen, lässt sich das Zwei-Länder-Modell in ein Summensystem, welches die Welt als Ganzes beschreibt, und in ein davon unabhängiges Differenzensystem, das Unterschiede in der Entwicklung beider Volkswirtschaften aufzeigt, transformieren. Dabei entspricht die Struktur des Summensystems dem neukeynesianischen Grundmodell geschlossener Volkswirtschaften (Neukeynesianische Makroökonomik geschlossener Volkswirtschaften, statisches Grundmodell), während das Differenzensystem formal zu dem neukeynesianischen Grundmodell offener Volkswirtschaften (Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell) äquivalent ist. Aus den komparativ-statischen Wirkungen, die von Schocks auf das Summen- und Differenzensystem ausgehen, lassen sich durch Übergang zur arithmetischen Mittelbildung der Wirkungen auf die einander entsprechenden Summen- und Differenzvariablen die Wirkungen in den einzelnen Ländern ermitteln (Neukeynesianisches Zwei-Länder-Modell, Wirkungen von Schocks). Eine analoge Lösungsmethode lässt sich auch für die Analyse symmetrischer neukeynesianischer Modelle einer Zwei-Länder-Währungsunion anwenden (Neukeynesianische Makroökonomik, statisches Modell einer Währungsunion).
2. Gesamtmodell: a) Unter Zugrundelegung der Notation für das statische neukeynesianische Modell einer kleinen offenen Volkswirtschaft besteht das analoge Zwei-Länder-Modell nachfrageseitig aus den beiden symmetrischen IS-Gleichungen (in logarithmisch-linearer Formulierung)
In der inländischen IS-Gleichung (1) hängt der Output () bzw. die Outputlücke (
) negativ vom Realzins (
) und vom internationalen Preisverhältnis - ausgedrückt in Änderungsraten (
) – sowie positiv von der Outputlücke des Auslands (
) und einem Nachfrageschock (
) ab. Wird für die Ausgangslage von absoluter Kaufkraftparität ausgegangen, kann das (logarithmierte) Preisverhältnis
durch die Inflationsratendifferenz
ersetzt werden; dabei steht
für den flexiblen nominalen Wechselkurs in Preisnotierung (Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Modell). Mit den Abkürzungen
für die in- bzw. ausländische Outputlücke (d.h. die Differenz zwischen tatsächlichem und natürlichem Output),
für den in- bzw. ausländischen Realzins (Fisher-Gleichung)
für den natürlichen Realzins und
für die Terms of Trade (mit ) können die IS-Gleichungen auch in der kompakten Form
dargestellt werden.
b) Es wird von vollkommener Kapitalmobilität zwischen den beiden Volkswirtschaften ausgegangen, sodass die Bedingung für die ungedeckte Zinsparität (Uncovered Interest Parity-Bedingung UIP)
gilt. Dabei steht bzw.
für den in- bzw. ausländischen Nominalzins,
für die erwartete Wechselkursänderungsrate und
für einen Risikoaufschlag für inländische Bonds. Die UIP-Bedingung (9) lässt sich mithilfe der Realzinsdefinition (4) in eine reale UIP-Bedingung der Form
überführen; dabei wird unterstellt, dass die Anleger mit einer schnellen Rückkehr ins Kaufkraftparitätengleichgewicht der Ausgangslage rechnen:
c) Für die Zinssteuerung der in- bzw. ausländischen Zentralbank wird eine Zinsregel vom Taylor-Typ (Taylor Rule TR) unterstellt, die der entsprechenden Regel im Fall der kleinen offenen Volkswirtschaft (Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell) entspricht:
Dabei gilt (Taylor-Prinzip) und
. Die angestrebte Zielinflationsrate der in- bzw. ausländischen Zentralbank wird mit
bzw.
bezeichnet. Durch die Zinsregel wird das Steuerungsinstrument der Zentralbank – der Nominalzins – an die Inflations- und Outputlücke gekoppelt. Alternativ wäre auch ein Regime der diskretionären Zinssteuerung vorstellbar. Die Taylorregeln TR und TR* lassen sich auch mithilfe des durch (4) gegebenen Realzinses
bzw.
ausdrücken:
Diese stellen Realzinsregeln dar, falls die in- bzw. ausländische Inflationserwartung mit dem Target Level bzw.
übereinstimmt.
d) Die Angebotsseite der in- bzw. ausländischen Volkswirtschaft ist durch Inflationsgleichungen vom Phillips-Kurven-Typ (Phillips Curves PC) gegeben:
mit und
. Die inländische Inflationsrate wird bestimmt durch die Inflationserwartung (
), die Outputlücke (
), importierte Inflation (
) und durch Kostenschocks (
). Importierte Inflation tritt dann auf, wenn für die Produktion heimischer Güter Importprodukte aus dem Ausland benötigt werden und diese durch Preis- oder Wechselkurssteigerungen teurer werden. Eine analoge Inflationsgleichung gilt dann auch für die ausländische Volkswirtschaft. Die Phillips-Kurven PC und PC* lassen sich mithilfe der Terms-of-Trade-Gleichung (6) auch in der Form
darstellen. Das Gesamtmodell besteht dann aus den IS-Gleichungen (7) und (8), der UIP-Bedingung (10), den Taylorregeln (14) und (15) sowie den PC-Gleichungen (18) und (19). Das symmetrische Zwei-Länder-Modell lässt sich in zwei Teilsysteme kleinerer Dimension (ein Summensystem und ein Differenzensystem) überführen, die jeweils unabhängig voneinander lösbar sind und grafisch in einem - bzw.
-Diagramm veranschaulicht werden können. Diese Vorgehensweise entspricht der Lösungsmethode eines symmetrischen neukeynesianischen Modells einer Zwei-Länder-Währungsunion (Neukeynesianische Makroökonomik, statisches Modell einer Währungsunion).
3. Summensystem: a) Das Summensystem beschreibt die Zwei-Länder-Modell als Ganzes und entsteht aus der Summation der einander entsprechenden Gleichungen (IS+IS*, TR+TR*, PC+PC*). Es beschreibt eine geschlossene (insbes. wechselkursunabhängige) Volkswirtschaft und enthält nur Summenvariablen (wie ,
,
). Für das Summensystem gelten die Gleichungen
Setzt man für die Aggregatvariablen abkürzend
wird deutlich, dass das System (20)-(22) dem statischen neukeynesianischen Grundmodell geschlossener Volkswirtschaften (Neukeynesianische Makroökonomik geschlossener Volkswirtschaften, statisches Grundodell) entspricht und im Sonderfall (d.h. bei Vernachlässigung einkommensabhängiger Exporte sowie importierter Inflation) sogar mit diesem identisch ist.
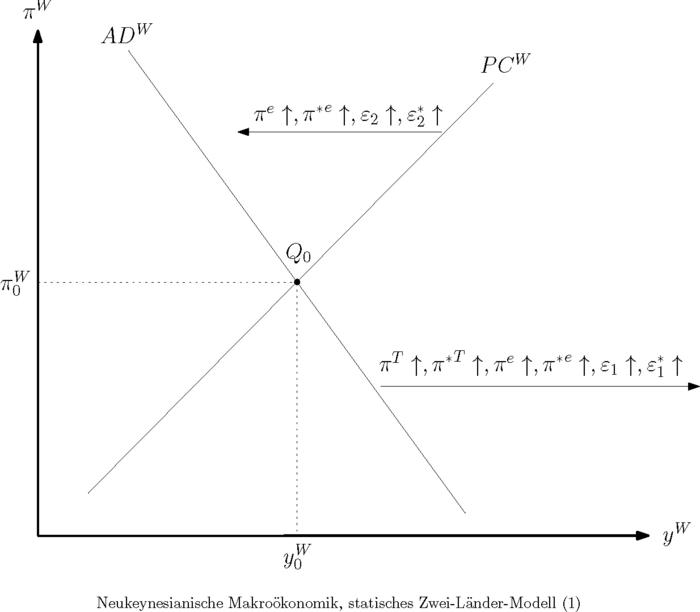
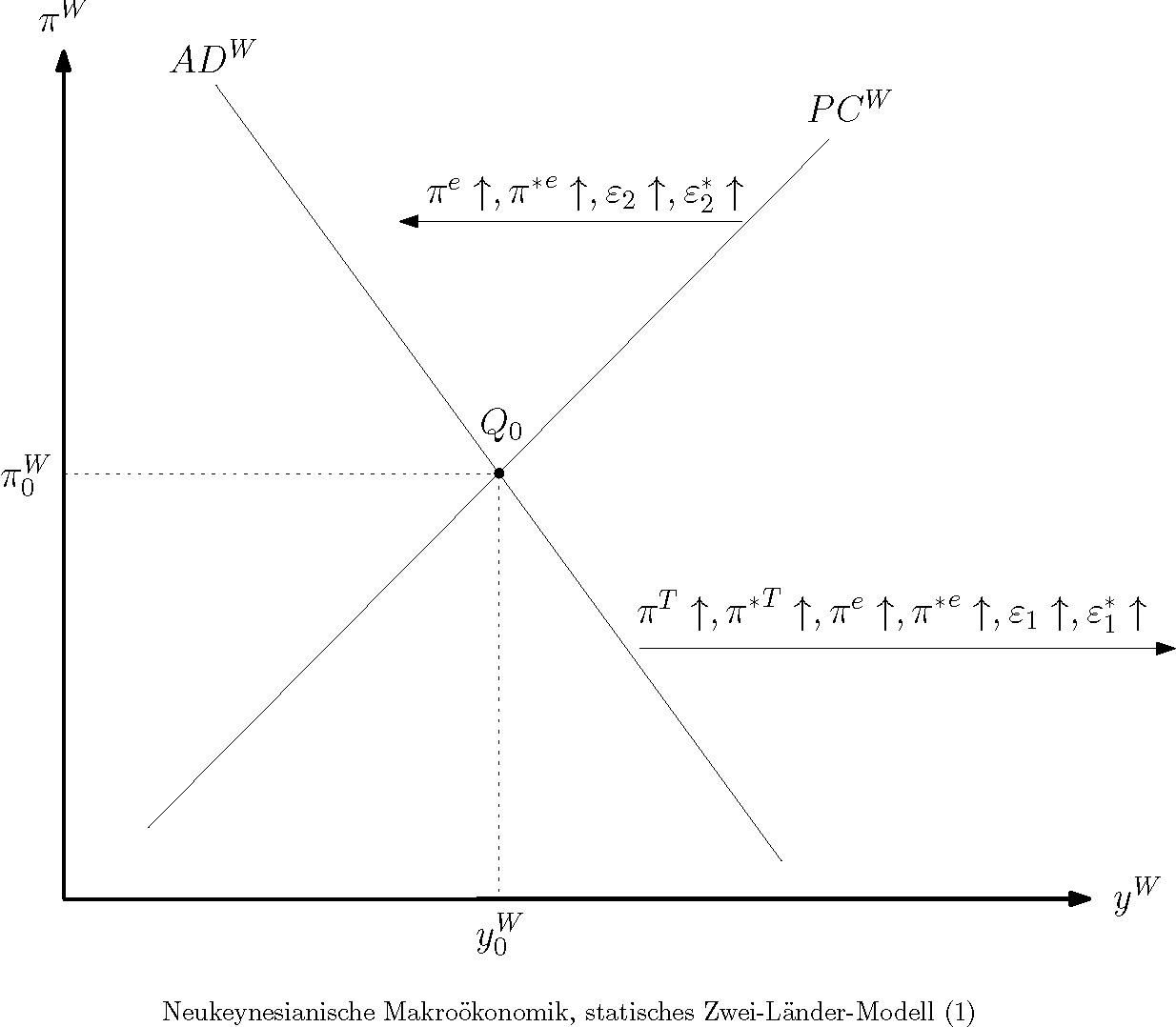
b) Grafisch ist das Summensystem in einem -Diagramm darstellbar (vgl. Abbildung "Neukeynesianische Makroökonomik, statisches Zwei-Länder-Modell (1)").
Dabei steht für den Weltoutput. Die Abbildung entspricht der grafischen Darstellung des statischen neukeynesianischen Grundmodells geschlossener Volkswirtschaften. Es enthält die fallend verlaufende aggregierte Nachfragekurve (Aggregate Demand) der Welt als Ganzes (ADW), die sich aus der Kombination der aggregierten IS-Kurve IS+IS* und der aggregierten Taylorregel TR+TR* ergibt. Für die ADW-Kurve gilt dann die Gleichung
oder gleichwertig dazu
Die ADW-Kurve enthält die Target Levels und
, die Inflationserwartungen
und
sowie die Störterme
und
als expansiv wirkende Lageparameter. Das
-Diagramm enthält außerdem die mit positiver Steigung verlaufende aggregierte Phillips-Kurve für die Welt als Ganzes (PCW). Diese ist durch die Gleichung
gegeben. Lageparameter sind die Inflationserwartungen und
sowie die Störterme
und
. Erhöht sich eine der beiden Inflationserwartungen oder eine der beiden Störgrößen, kommt es zu weltweiter Inflation, sodass sich die PCW-Kurve nach links verlagert.
c) Für die komparativ-statische Analyse inländischer Nachfrage- oder Angebotsschocks ( oder
) gilt, dass diese in Bezug auf das Summensystem die gleichen Wirkungen entfalten wie im statischen neukeynesianischen Grundmodell für die geschlossene Volkswirtschaft (Neukeynesianische Makroökonomik geschlossener Volkswirtschaften, statisches Grundmodell). Ein expansiver Nachfrageimpuls
verlagert die ADW-Kurve nach rechts und erhöht den Weltoutput
und die aggregierte Inflationsrate
. Gleichzeitig ist hiermit nach den Zinsregeln eine Steigerung des aggregierten Nominal- und Realzinssatzes verbunden, wodurch die durch den Nachfrageimpuls induzierte Steigerung von
und
wieder etwas abgedämpft wird. Ein Kostenschock (
) verschiebt die PCW-Kurve nach links und bewirkt Stagflation, d.h. erhöht die aggregierte Inflationsrate
bei gleichzeitigem Rückgang des Weltoutputs
. Nachfrageseitig ist die Outputkontraktion nur mit einer Realzinssteigerung erklärbar, die wiederum bei gegebenen Inflationserwartungen aus einer Zunahme des aggregierten Nominalzinssatzes resultiert. Nach der aggregierten Zinsregel (21) fällt dann aber die zinssteigernde Wirkung der Erhöhung der aggregierten Inflationsrate stärker aus als der zinssenkende Effekt, der aus der weltweiten Outputkontraktion resultiert.
d) Betrachtet man die Wirkungen einer (isolierten oder simultanen) Steigerung der Zielinflationsrate auf die Aggregatgrößen und
, so sind diese davon abhängig, ob damit eine parallele Anpassung der Inflationserwartungen verbunden ist oder nicht. Bleiben die Inflationserwartungen
und
unverändert, kommt es über die Realzinssenkung zu einer Rechtsverschiebung der ADW-Kurve, während die PCW-Kurve in der Lage unverändert bleibt. Es ergibt sich dann eine Erhöhung der weltweiten Inflation und des weltweiten Outputs. Die Outputsteigerung resultiert dabei aus einem Rückgang des aggregierten Realzinses
, welcher bei gegebenen Erwartungen gleichbedeutend mit einer Senkung des aggregierten Nominalzinses ist. Da das Taylor-Prinzip
unterstellt wurde, geht von der Anhebung des Target Levels
(oder
) nach der Zinsregel (12) (bzw. (13)) ein zinssenkender Effekt aus. Dieser fällt dann stärker aus als die zinssteigernden Wirkungen, die nach der Taylorregel von der Zunahme der Inflationsrate und des Outputs erzeugt werden. Andere Ergebnisse erhält man, wenn die Anhebung der Zielinflationsrate mit einer gleich großen Korrektur der Inflationserwartung nach oben verbunden ist. Es gilt jetzt
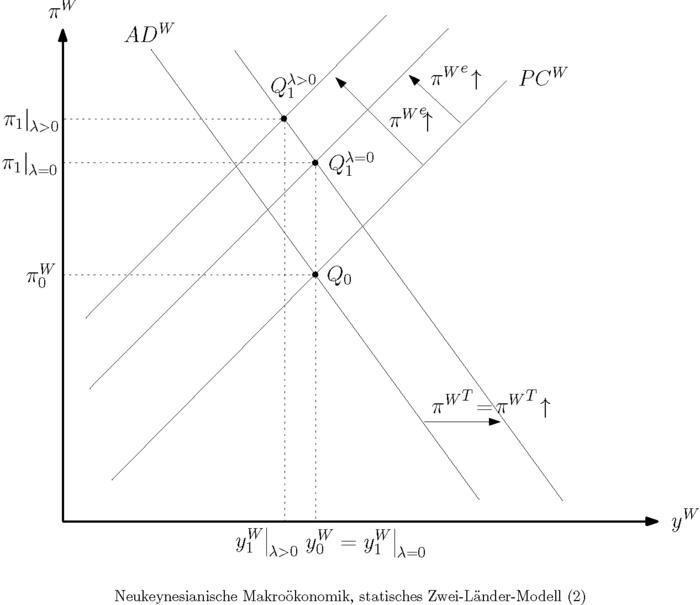
sodass es nach (25) über die damit verbundene Senkung des aggregierten Realzinses zu einer (im Vergleich zum Fall stärkeren) Rechtsverschiebung der ADW-Kurve kommt und gleichzeitig infolge der Anpassung der Inflationserwartung auch eine Linksverlagerung der PCW-Kurve stattfindet (vgl. "Abbildung Neukeynesianische Makroökonomik, statisches Zwei-Länder-Modell (2)").
Es ergeben sich dann stärkere Inflationseffekte als im Fall konstanter Inflationserwartungen. Im Sonderfall (d.h. bei Vernachlässigung importierter Inflation in den Inflationsgleichungen (16) und (17)) bewirkt die geldpolitische Lockerung durch die Erwartungsanpassung klassische Resultate (Neukeynesianische Makroökonomik geschlossener Volkswirtschaften, statisches Grundmodell). Es kommt dann im Summensystem lediglich zu proportionalen Inflations- und Nominalzinseffekten, während das Outputniveau und der Realzins konstant bleiben. Es gilt also im Fall
sowie
:
und
In diesem Sonderfall liegt das Endgleichgewicht () im
-Diagramm vertikal über dem Ausgangsgleichgewicht
auf den neuen, nach rechts verschobenen Nachfragekurve ADW. Wird dagegen importierte Inflation in den Phillips-Kurven berücksichtigt (Fall
), findet neben der Erwartungsanpassung ein zusätzlicher (endogener) Kostenschock statt, der in jedem Land die Inflationsrate weiter ansteigen lässt, sodass sich – grafisch gesprochen – eine stärkere Linksverschiebung der aggregierten PC-Kurve ergibt als im Sonderfall
. Die Folge ist ein stagflationäres Resultat, d.h. eine überproportionale Steigerung der aggregierten Inflationsrate bei gleichzeitiger Senkung des Weltoutputs. Es gilt also im Fall
was grafisch einem Endgleichgewicht () nordwestlich des Gleichgewichts ohne Berücksichtigung importierter Inflation (
) entspricht. Es muss dann zu einer Realzinssteigerung (
) gekommen sein, um die Outputkontraktion nachfrageseitig erklären zu können. Nach der Realzinsdefinition gemäß der Fisher-Gleichung (4) tritt die Erhöhung von
genau dann auf, wenn der aggregierte Nominalzins stärker als die aggregierte Zielinflationsrate gestiegen ist.
4. Differenzensystem: a) Das Differenzensystem beschreibt Unterschiede in der Entwicklung beider Länder, die sich infolge asymmetrischer Schocks (wie z.B. eines einseitigen Nachfrageimpulses) ergeben. Es besteht aus der Differenz der IS-Gleichungen (IS-IS*), der ungedeckten Zinsparitätenbedingung (UIP), der Differenz der Taylorregeln (TR-TR*) und der Differenz der Inflationsgleichungen (PC-PC*). Es gilt dann das Gleichungssystem
Außerdem gilt nach Gleichung (6) für die Terms of Trade :
Setzt man für die Differenzvariablen abkürzend
wird deutlich, dass das System (31)-(35) dem statischen neukeynesianischen Grundmodell für die offene Volkswirtschaft (Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell) entspricht und im Sonderfall sogar mit diesem identisch ist. Im Fall
, d.h. bei Berücksichtigung importierter Inflation, ergibt sich ein (geringfügiger) Unterschied zum neukeynesianischen Grundmodell, der darin besteht, dass jetzt die Phillips-Kurven-Gleichung PCD vom nominalen Wechselkurs
abhängig ist. Durch Einsetzen der Terms of Trade-Gleichung (35) in (34) gilt nämlich
woraus die Wechselkursabhängigkeit der PCD-Gleichung im Falle ersichtlich wird.
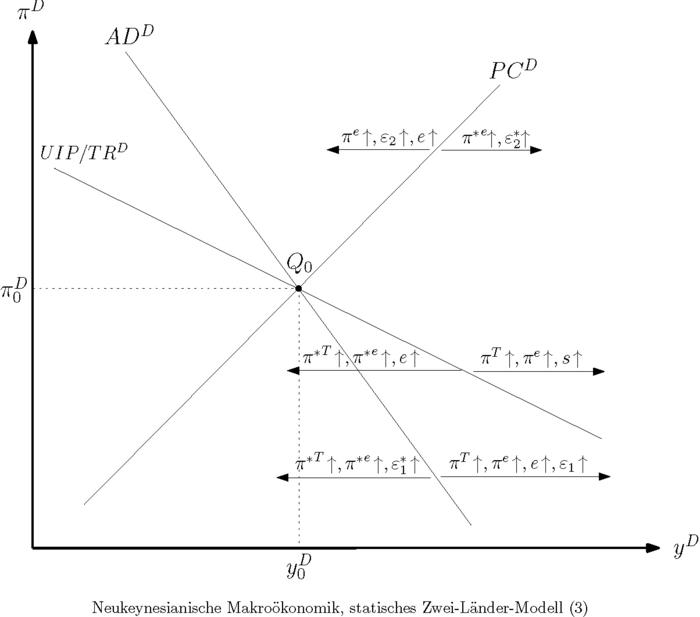
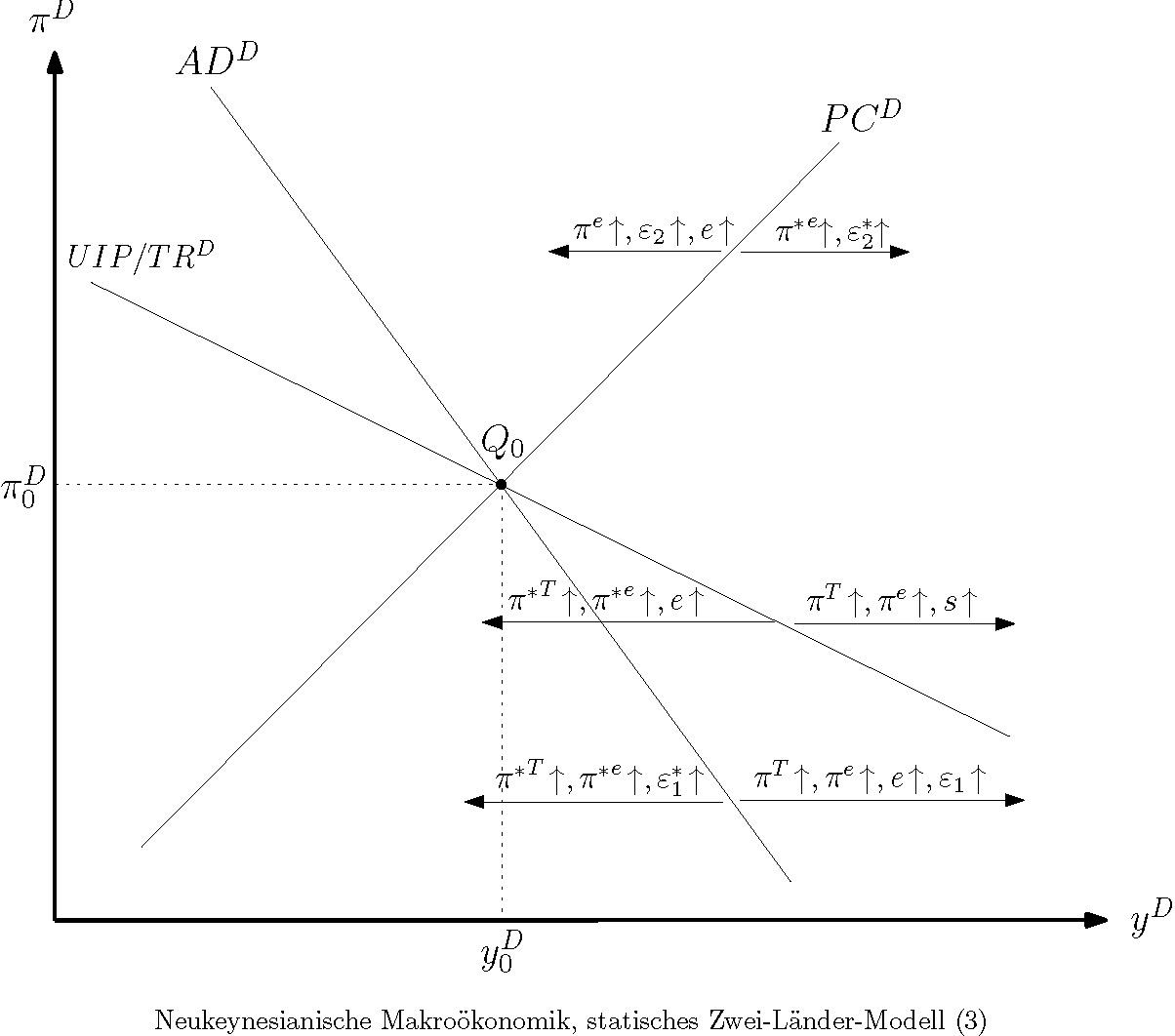
b) Grafisch ist das Differenzensystem in einem -Diagramm darstellbar (vgl. Abbildung "Neukeynesianischer Makroökonomik, statisches Zwei-Länder-Modell (3)").
Dabei steht für die Outputdifferenz. Die Abbildung entspricht im Wesentlichen der graphischen Darstellung des statischen neukeynesianischen Grundmodells offener Volkswirtschaften. Die fallend verlaufende aggregierte Nachfragekurve des Differenzensystems (ADD) ergibt sich aus der Kombination der (IS-IS*)- und (TR-TR*)-Gleichung und hat die Darstellung
oder gleichwertig dazu
Dabei kann , d.h. die Differenz der natürlichen Outputniveaus
und
, aufgrund der Symmetrieannahme gleich null gesetzt werden. Die ADD-Kurve enthält die Zielinflationsraten
und
, die Inflationserwartungen
und
, den nominalen Wechselkurs
und die Störterme
und
als Lageparameter. Eine Steigerung von
oder
senkt die Realzinsdifferenz
und erhöht die Outputdifferenz
, sodass sich die ADD-Kurve nach rechts verlagert. Ebenso wird durch eine Abwertung der Inlandswährung
oder durch einen expansiven inländischen Nachfrageimpuls (
) die ADD-Kurve nach rechts verschoben. Entsprechend ergibt sich eine Linksverlagerung der ADD-Kurve, wenn die Auslandsgrößen
,
und
zunehmen. Das
-Diagramm enthält weiter die ebenfalls fallend verlaufende UIP/TRD-Kurve, die aus der Kombination der UIP-Bedingung (32) und der Differenz der Taylorregeln (33) resultiert. Wegen der Gleichheit der natürlichen Realzinsen
und
(gemäß Gleichung (5)) ergibt sich zusammen mit der Terms of Trade-Gleichung (35) die Gleichung
bzw.
Lageparameter der UIP/TRD-Kurve sind – wie schon bei der Nachfragekurve ADD – die Target Levels und
, die Inflationserwartungen
und
, der nominale Wechselkurs
und zusätzlich der Risikoprämienschock
. Durch eine Steigerung von
,
oder
verlagert sich die UIP/TRD-Kurve nach rechts, während sich eine Linksverschiebung im Falle einer Erhöhung von
,
oder des Wechselkurses
ergibt. Es kann unterstellt werden, dass die UIP/TRD-Kurve flacher als die ADD-Kurve im
-Diagramm verläuft. Vergleicht man die Steigungen der UIP/TRD- und ADD-Kurve, die sich aus (41) und (39) ergeben, ergibt sich als Bedingung für einen flacheren Verlauf der UIP/TRD-Kurve die Ungleichung
welche erfüllt ist, wenn in den Taylorregeln der (über dem Wert eins liegende) Koeffizient im Vergleich zum zweiten Koeffizienten
hinreichend groß ausfällt. Ökonomisch legen dann die Zentralbanken ein relativ starkes Gewicht auf die Inflationsstabilisierung. Als dritte Kurve im
-Diagramm ist schließlich noch die mit positiver Steigung verlaufende und durch (37) gegebene PCD-Kurve zu berücksichtigen. Sie enthält als Lageparameter die Inflationserwartungen
und
, die Störvariablen
und
sowie im Fall
(d.h. bei Berücksichtigung importierter Inflation in den Inflationsgleichungen) den Wechselkurs
. Eine Steigerung von
,
und
führt zu einem positiven, eine Erhöhung von
und
zu einem negativen Inflationsgefälle. Daraus resultieren dann Verschiebungen der PCD-Kurve nach links bzw. rechts.
c) Hinsichtlich der komparativ-statischen Wirkungen isolierter inländischer Nachfrage- oder Angebotsschocks ( ,
) gilt, dass diese – bei Vernachlässigung importierter Inflation (
) – in Bezug auf das Differenzensystem mit den entsprechenden Wirkungen im statischen neukeynesianischen Modell für die offene Volkswirtschaft (Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell) übereinstimmen. Für den Sonderfall
gelten dann auch vollkommen analoge Abbildungen im
-Diagramm. Im Fall
(d.h. bei Berücksichtigung importierter Inflation) ist dagegen zusätzlich noch die wechselkursbedingte Verschiebung der PCD-Kurve zu berücksichtigen. Wird unterstellt, dass die durch Wechselkursänderungen induzierten Effekte auf die Inflationsdifferenz
vergleichsweise schwach sind, bleiben aus qualitativer Sicht die komparativ-statischen Wirkungen von Störungen im Differenzensystem durch den Übergang von
zu
unverändert. Überträgt man die Effekte, die von Störungen im Rahmen des statischen neukeynesianischen Modells für die kleine offene Volkswirtschaft ausgehen, auf das vorliegende Differenzensystem, ergeben sich folgende Resultate: Ein unilateraler Nachfrageimpuls (
) verlagert die ADD-Kurve nach rechts und bewirkt ein reales und nominales Konjunkturgefälle zwischen beiden Ländern:
Dieses entsteht trotz der Zunahme der Realzinsdifferenz und der realen Aufwertung der Inlandswährung
Durch die nominale Aufwertung der Inlandswährung () wird auch die UIP/TRD-Kurve nach rechts verschoben, während dadurch die ADD-Kurve wieder etwas zurückverlagert wird. Das Endgleichgewicht Q1 liegt dann nordöstlich vom Anfangsgleichgewicht Q0. Im Sonderfall
würde dabei der Punkt Q1 auf der in der Lage unveränderten PCD-Kurse liegen. Im Fall
wäre dagegen auch die durch Wechselkursänderungen hervorgerufene Verschiebung der PCD-Kurve zu berücksichtigen, die durch die Aufwertung der Inlandswährung etwas nach unten verschoben wird. Das Endgleichgewicht würde dann auf der neuen PCD-Kurve liegen. Das Inflationsgefälle (d.h. der Anstieg von
) wäre jetzt im Vergleich zum Fall
weniger stark ausgeprägt, während sich das Outputgefälle (d.h. die Zunahme der Outputdifferenz
) wegen der geringeren Steigerung der Realzinsdifferenz weiter verstärken würde. Tritt ein isolierter Kostenschock auf (
), ergibt sich für das Differenzensystem wieder ein stagflationäres Resultat, d.h. ein Rückgang der Outputdifferenz bei gleichzeitiger Steigerung der Inflationsdifferenz:
Das negative reale Konjunkturgefälle ist dabei auf die Erhöhung der Realzinsdifferenz und der damit verbundenen realen Aufwertung der Inlandswährung zurückzuführen. Verläuft die ADD-Kurve steiler als die UIP/TRD-Kurve (d.h. gilt Bedingung (42)), kommt es auch zu einer nominalen Aufwertung der inländischen Währung. Grafisch gesprochen wird dadurch im Fall die durch den Kostenschock hervorgerufene Linksverlagerung der PCD-Kurve wieder etwas abgeschwächt, sodass auch das Konjunkturgefälle zwischen beiden Ländern weniger stark ausgeprägt ist als im Fall
. Wird ein Anstieg der Risikoprämie für die Haltung inländischer Bonds betrachtet (
), ergibt sich über die Abwertung der Inlandswährung ein positives Output- und Inflationsgefälle. Da die Realzinsdifferenz gestiegen ist, lässt sich die Erhöhung der Outputdifferenz nur über eine reale Abwertung der Inlandswährung erklären. Es geht also insgesamt im Fall
:
,
Grafisch findet dann eine Verschiebung der ADD-Kurve nach rechts und insgesamt auch eine Rechtsverlagerung der UIP/TRD-Kurve statt. Bei Berücksichtigung importierter Inflation in den Phillips-Kurven (d.h. im Fall ) verlagert sich die PCD-Kurve abwertungsbedingt etwas nach oben mit der Folge einer im Vergleich zum Fall
Verstärkung der Inflations- und Abschwächung der Outputdifferenz.
d) Eine weitere Störung des Differenzensystems ist eine einseitige Anhebung der Zielinflationsrate , wobei zwischen dem Fall der gleichzeitigen Anpassung der zugehörigen Inflationserwartung (
) und dem Fall der Nichtanpassung der Inflationserwartung (
) zu unterscheiden ist. Ohne Erwartungsanpassung ergibt sich aus Sicht des aktiven Landes ein positives reales und nominales Konjunkturgefälle, welches aus dem Rückgang des Nominal- und Realzinsdifferenzials und der nominalen und realen Abwertung der Inlandswährung resultiert. Es gilt also im Fall
sowie
:
Grafisch wird die UIP/TRD-Kurve im -Diagramm durch die geldpolitische Lockerung weiter nach rechts verschoben als die ADD-Kurve, sodass eine nominale Abwertung (
) erforderlich ist, um ein simultanes Gleichgewicht zu erhalten. Bei Berücksichtigung importierter Inflation in den Phillips-Kurven (
) wird dadurch die PCD-Kurve etwas nach links verlagert, sodass im Vergleich zum Fall
das Inflationsgefälle verstärkt und das Outputgefälle abgeschwächt wird. Tritt zugleich mit der einseitigen Anhebung der Zielinflationsrate eine gleich große Korrektur der Inflationserwartung auf (
), wird das durch die einseitige geldpolitische Lockerung erzeugte Inflationsgefälle weiter verstärkt und das Outputgefälle weiter abgeschwächt. Im Sonderfall
ergeben sich dann für das Differenzensystem klassische Resultate, d.h.
und
Wird dagegen importierte Inflation in den Phillips-Kurven berücksichtigt (), verstärkt sich das Inflationsgefälle im Vergleich zum Fall
und wird das Outputdifferenzial negativ, sodass sich für das Differenzensystem ein stagflationäres Resultat ergibt:
Vgl. zugehöriger Schwerpunktbeitrag Neukeynesianische Makroökonomik.
Literaturhinweise SpringerProfessional.de
Bücher auf springer.com
Interne Verweise
Neukeynesianische Makroökonomik, statisches Zwei-Länder-Modell
Neukeynesianische Makroökonomik, statisches Zwei-Länder-Modell
- Fisher-Gleichung
- Fisher-Gleichung
- Neukeynesianische Makroökonomik
- Neukeynesianische Makroökonomik geschlossener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik geschlossener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik geschlossener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik geschlossener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik offener Volkswirtschaften, statisches Grundmodell
- Neukeynesianische Makroökonomik, statisches Modell einer Währungsunion
- Neukeynesianische Makroökonomik, statisches Modell einer Währungsunion
- Neukeynesianisches Zwei-Länder-Modell, Wirkungen von Schocks
- Phillips-Kurve
- Produktionslücke
- Zinsparität