Konsumfunktion
Übersicht
zuletzt besuchte Definitionen...
Darstellung der funktionalen Abhängigkeit der Konsumausgaben von verschiedenen Einflussfaktoren wie Einkommen, Preise, Vermögen, Zinsniveau.
1. Annahmen über die Bestimmungsgründe der Konsumnachfrage (Konsumhypothesen) stellen aufgrund der Aufteilung des Einkommens (Y) auf Konsum (C) und Sparen (S), d.h. Y = C + S, zugleich Hypothesen über das Sparverhalten dar. Die einfachste Konsumhypothese besagt, dass der Konsum vom laufenden Einkommen abhängt, und zwar so, dass mit steigendem Einkommen die Konsumnachfrage steigt:
C = C(Y),
mit 0 < dC/dY < 1. Die Ableitung dC/dY repräsentiert die marginale Konsumquote (c). Wegen Y = C + S folgt die Sparfunktion:
S = Y - C(Y) = S(Y).
2. Verläufe: a) Keynes unterstellte einen speziellen Verlauf der Konsumfunktion: Nach seinem „fundamentalen psychologischen Gesetz” nimmt der Konsum mit steigendem Einkommen zu, allerdings nur unterproportional. Ferner ging Keynes davon aus, dass die durchschnittliche Konsumquote (C/Y) mit steigendem Einkommen sinkt. Keynes betrachtete das Sparen als Luxus und nahm daher an, dass die Reichen einen höheren Anteil ihres Einkommens sparen können als die Armen.
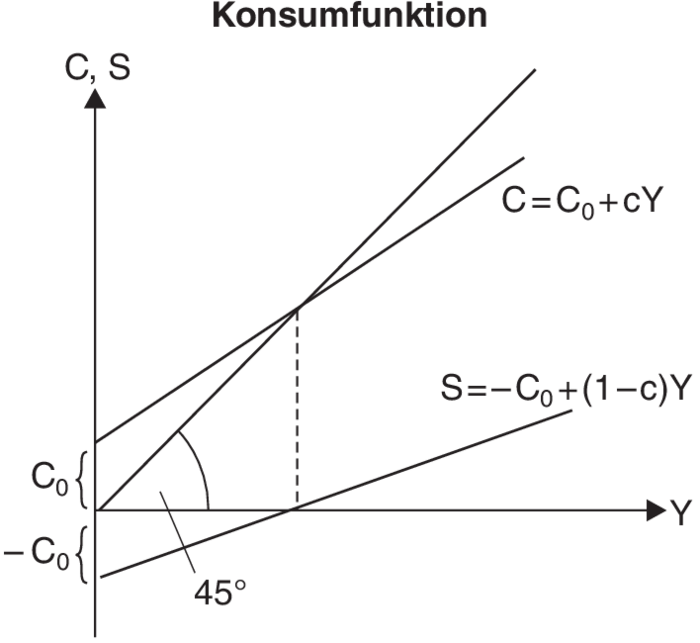
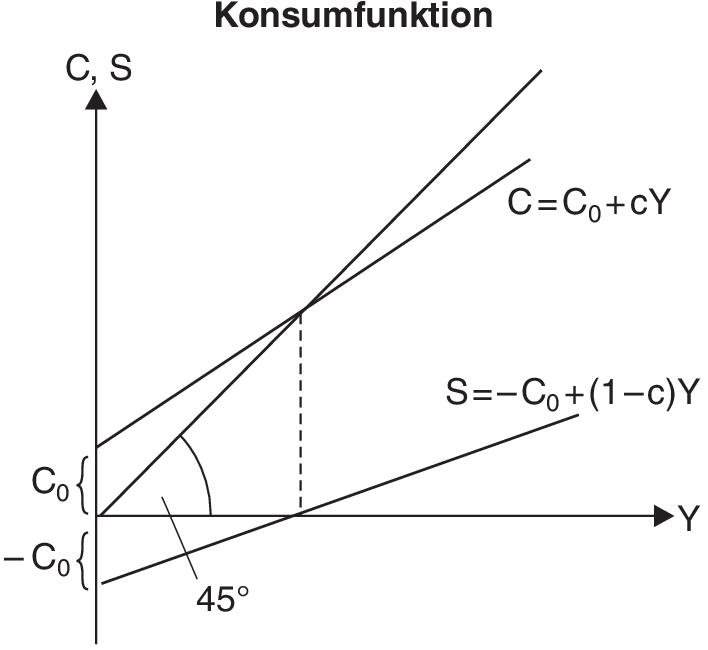
b) Vereinfachend wird für die grafische Analyse häufig mit einer linearen Konsumfunktion gearbeitet:
C = C0 + cY,
mit C0 = Basiskonsum oder autonomer Konsum > 0, 0 < c = konstant < 1. Diese Konsumfunktion ist mit dem psychologischen Gesetz von Keynes vereinbar, denn für die marginale Konsumquote gilt:
dC / dY = c < 1
und für die durchschnittliche
C / Y = C0 / Y + c.
Dabei nimmt C / Y bei positivem Basiseinkommen mit wachsendem Einkommen ab. Grafisch ergibt sich die Darstellung „Konsumfunktion”.
3. Empirische Untersuchungen (v.a. von Kuznets, 1946) zeigen eine langfristig konstante durchschnittliche Konsumquote. Erklärungen:
(1) Relative Einkommenshypothese;
(2) permanente Einkommenshypothese (permanentes Einkommen);
(3) Lebenszyklushypothese (Lebenszeit-Einkommenshypothese). Neben dem in den letzten Ansätzen als Konsumdeterminante berücksichtigten Vermögen wird in der Literatur darüber hinaus ein spezifischer realer Vermögenseffekt diskutiert, der das Konsumverhalten im Konjunkturverlauf stabilisiert (Pigou, 1941): Bei einem Anstieg des realen Vermögensbestandes durch eine Preissenkung (etwa im Abschwung) steigen die Konsumausgaben bei gegebenem Einkommen, weil das geplante Sparen reduziert werden kann. Dadurch wird der Abschwung gebremst.
4. Die Abhängigkeit der Konsumquote von der Einkommensverteilung wird auf Keynes zurückgeführt und wurde von Kaldor formalisiert. Die Konsumausgaben (C) bestehen aus:
(1) Ausgaben aus Lohneinkommen (CL = cL L) und
(2) Ausgaben aus Gewinneinkommen (CG = cG G); es gilt:
C = cL L + cG G.
Mit der Verteilungsgleichung Y = L + G folgt:
C = (cL - cG) L + cGY
C = [ (cL - cG) L / Y + cG] Y.
Dabei ist der Ausdruck in der eckigen Klammer die von der Lohnquote (L / Y) abhängige Konsumquote, wobei gilt:
0 < cG < cL < 1.
Mit steigender Lohnquote L/Y steigen die Konsumausgaben (Kaufkrafteffekt).
5. Dynamische Funktionen: In dynamischen Modellen (dynamische Makroökonomik) werden verschiedene zeitliche Verzögerungen (Lags) in die Konsumfunktion eingebaut. Zudem wird zwischen kurz- und langfristigen Funktionen unterschieden, wobei angenommen wird, dass die kurzfristige Konsumfunktion flacher als die langfristige verläuft, was der relativen Einkommenshypothese entspricht. Außerdem kann der laufende Konsum auch vom zukünftig erwarteten Konsum und vom Realzins abhängen, wenn die Konsumnachfrage aus einem intertemporalen Nutzenmaximierungsansatz abgeleitet wird.
Vgl. zugehöriger Schwerpunktbeitrag Makroökonomische Totalmodelle geschlossener Volkswirtschaften.
Literaturhinweise SpringerProfessional.de
Bücher auf springer.com
Interne Verweise
Konsumfunktion
- autonomer Konsum
- Einkommenshypothesen
- Konsumhypothesen
- Konsumquote
- makroökonomische Totalmodelle geschlossener Volkswirtschaften
- makroökonomische Totalmodelle geschlossener Volkswirtschaften, Nachfrageseite
- marginale Sparquote
- mikroökonomische Fundierung der makroökonomischen Theorie
- permanentes Einkommen
- psychologisches Gesetz
- Ratchet Effect
- relative Einkommenshypothese
- Sparfunktion
- Staatsausgabenmultiplikator
- Vermögenseffekt des Geldes