Neukeynesianische Makroökonomik, optimale geldpolitische Reaktion

1. Charakterisierung: Im Rahmen der dynamischen Grundmodells der Neuen Keynesianischen Makroökonomik (NKM) (Neukeynesianische Makroökonomik, dynamisches Grundmodell) lässt sich die Frage der in Bezug auf eine Wohlfahrtsverlustfunktion optimalen (verlustminimierenden) geldpolitischen Reaktion auf Kostenschocks analysieren. Dabei wird eine quadratische Verlustfunktion der Zentralbank zugrunde gelegt, die der Zielsetzung des flexible inflation targeting genügt:

wobei

V_t = Verlustindex in t

E_t = rationaler Erwartungsoperator

β = Diskontfaktor (0< β <1)

π_t = Inflationsrate,

π^T = Zielinflationsrate (Target Rule)

x_t = Outputlücke

λ = Gewichtungsfaktor (λ ≥ 0).

Die Zentralbank verfolgt als primäres Ziel die Stabilisierung der Inflationsrate π auf dem Target Level π^T (welche in numerischen Simulationen immer gleich null gesetzt wird). Im Falle λ>0 strebt sie auch eine geschlossene Outputlücke (x_t = 0) an, was gleichbedeutend mit der Outputstabilisierung auf dem langfristigen (Flexpreis-)Outputniveau ist. Im Sonderfall λ = 0 wird nur die Stabilisierung der Inflationsrate (strict inflation targeting) als einziges Ziel angestrebt. In der intertemporalen Verlustfunktion (1) werden zukünftige quadratische Inflations- bzw. Outputlücken mit einem Diskontfaktor β auf die Gegenwartsperiode t diskontiert. Im Sonderfall β = 1 (keine Diskontierung) ist zur skalierten Verlustfunktion (1-β)V_t überzugehen, die im Unterschied zu V_t auch für β → 1 endliche Werte annimmt und gegen die gewichtete Summe der unbedingten Varianzen Var(π_t)+λVar(x_t) konvergiert. Außerdem bleiben durch die Skalierung mit 1-β die Bedingungen erster Ordnung für ein Verlustminimum unverändert. Diese resultieren aus der Minimierung von V_t unter Beachtung der IS- und Phillips-Kurven-Gleichung des dynamischen NKM-Modells (Neukeynesianische Makroökonomik, dynamisches Grundmodell). Solange die Zentralbank kein zusätzliches Zinsstabilisierungsziel verfolgt, stellt die IS-Gleichung nur eine Bestimmungsgleichung für den optimalen Instrumenteneinsatz dar, sodass nur die Inflationsgleichung

als einzige Nebenbedingung zu beachten ist. Über die zugehörige Lagrange-Funktion

mit dem Lagrange-Multiplikator (Schattenpreis, Multiplier) μ_t+k lassen sich dann die Bedingungen erster Ordnung (First Order Conditions (FOC)) angeben, indem diese nach π_t, x_t und μ_t abgeleitet wird und die partiellen Ableitungen jeweils gleich null gesetzt werden. Dabei wird eine optimale unrestringierte Geldpolitik unter timeless perspective commitment unterstellt, d.h. eine glaubwürdige Selbstverpflichtung auf die Regelbindung, die bereits in der weit zurückliegenden Vergangenheit getroffen wurde, sodass die Bedingung erster Ordnung in der Anfangsperiode vernachlässigt werden kann. Man erhält dann für k = 0, 1 aus (3) die FOC

Dann gilt mit Δμ_t=μ_t-μ_t-1 und Δ x_t = x_t-x_t-1 durch Elimination des Multiplikators die Zielregel (targeting rule)

bzw.

Die optimale geldpolitische Reaktion auf einen Kostenschock lässt sich im Regime Commitment durch eine Zielregel (eine Beziehung zwischen den Zielvariablen π und x) darstellen, die die Instrumentenregel vom Taylor-Typ

aus dem dynamischen NKM-Modell ersetzt. Dabei steht i_t für den Nominalzins (Nominal Interest Rate). Dadurch ergibt sich ein kleinerer Verlustindex (Wert der Zielfunktion V) als unter der Taylor-Regel (8). Die targeting rule (7) gilt im Falle der rein vorausschauenden Phillips-Kurve (2) und ist durch die Eigenschaft der history dependence gekennzeichnet. Das bedeutet, dass der optimale (verlustminimierende) Verlauf der Inflationsrate π_t in negativer Weise an die Outputlückenänderung (Δ x_t) gekoppelt ist und somit auch von der vergangenen Outputentwicklung abhängt. Da ein temporärer Kostenschock zunächst mit Stagflation (d.h. einer positiven Inflationsrate bei gleichzeitig negativer Outputlücke) verbunden ist und die Outputlücke im Zuge der Anpassung wieder ansteigt (d.h. x_t > x_t-1 für hinreichend großes t), muss nach der targeting rule (7) aus einer zunächst positiven eine negative Inflationslücke werden, sodass im Laufe der Anpassung Deflation auftritt und dann das Preisniveau (Price Level)

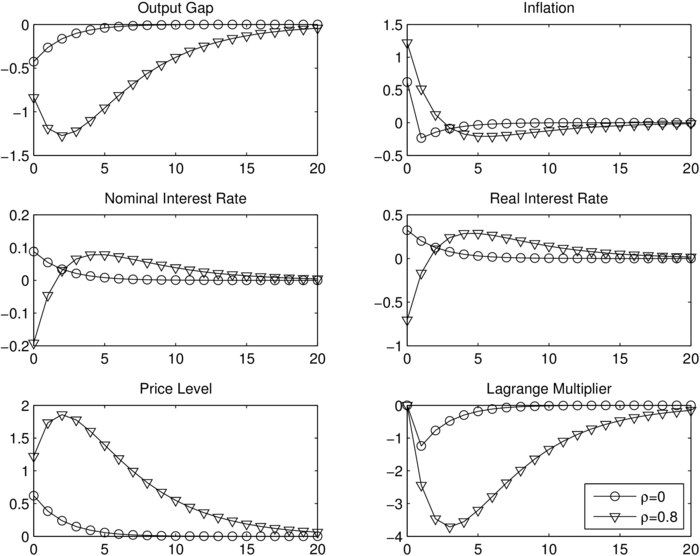
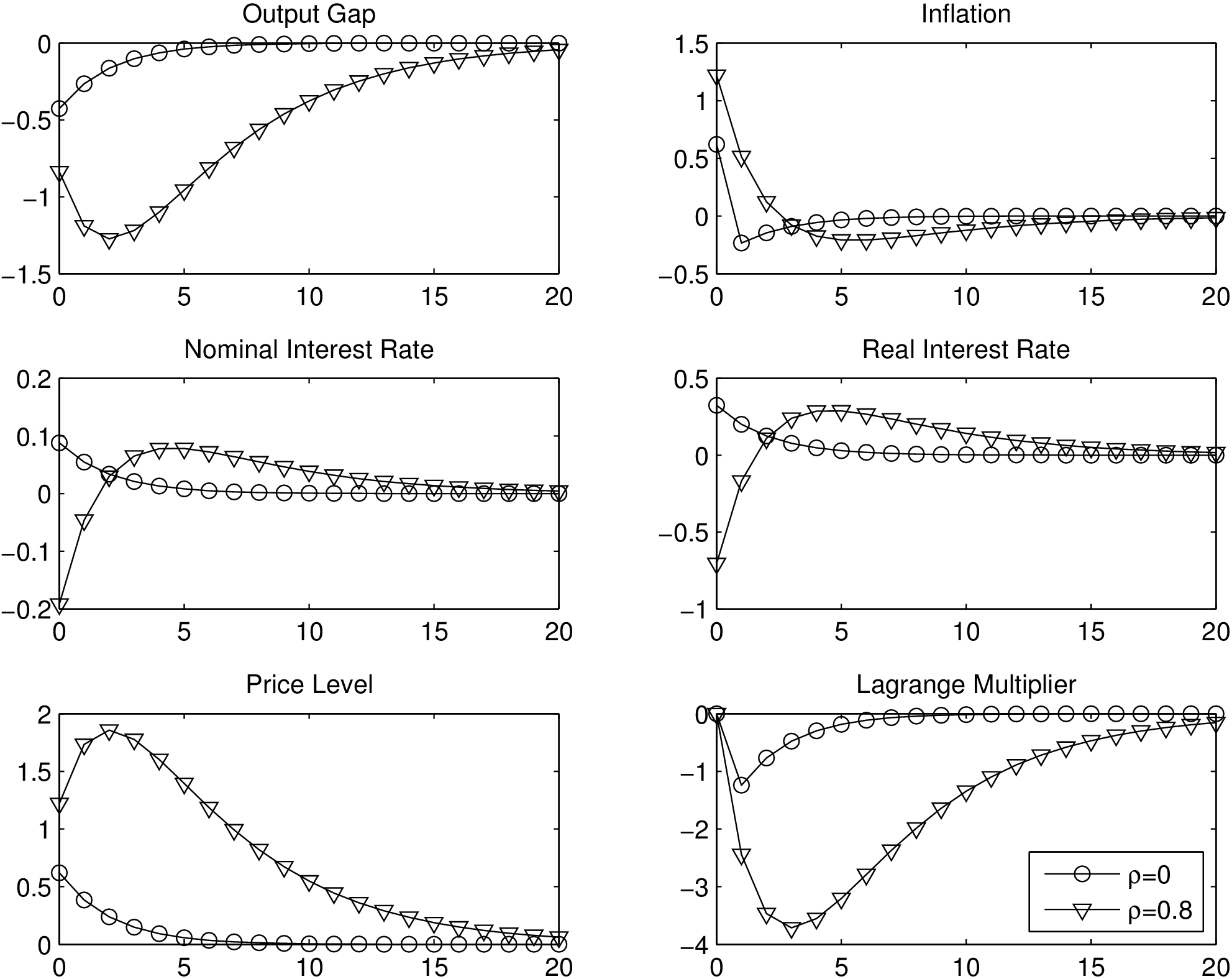
langfristig in seinen Anfangszustand zurückkehrt, also nicht dauerhaft durch den Kostenschock ansteigt (vgl. Abbildung „Kostenschock und optimale geldpolitische Reaktion im NKM-Modell“).

Bild in Originalgröße zeigen

„Kostenschock und optimale geldpolitische Reaktion im NKM-Modell“ 

Auch im Sonderfall, dass der Kostenschock keine Persistenz aufweist (One-off-Schock), ergibt sich – im Unterschied zur Zinsregel vom Taylor-Typ (Neukeynesianische Makroökonomik, dynamisches Grundmodell) – ein lang  anhaltender (persistenter) Anpassungsprozess in der Inflationsrate und Outputlücke. Dies ist auch daran erkennbar, dass sich das System unter optimaler Kontrolle, d.h. die Inflationsgleichung (2) in Kombination mit der Zielregel (7) in eine hybride Differenzengleichung in x_t überführen lässt, die neben einem instabilen auch einen stabilen Eigenwert enthält, sodass der Anpassungsprozess in π_t und x_t unter der optimalen unrestringierten Geldpolitik auch eine intrinsische Dynamik beinhaltet.

2. Optimale einfache Regeln: Da die optimale Geldpolitik unter Commitment durch eine targeting rule abgebildet werden kann, die die Eigenschaft der history dependence aufweist, ist es naheliegend, die optimale unrestringierte Geldpolitik durch Instrumentenregeln vom Taylor-Typ zu approximieren, die genau diese Eigenschaft reproduzieren können. Hierzu zählen Zinsregeln mit Glättung (smoothing), bei denen der aktuelle Zinssatz auch vom vergangenen Zinssatz abhängig ist:

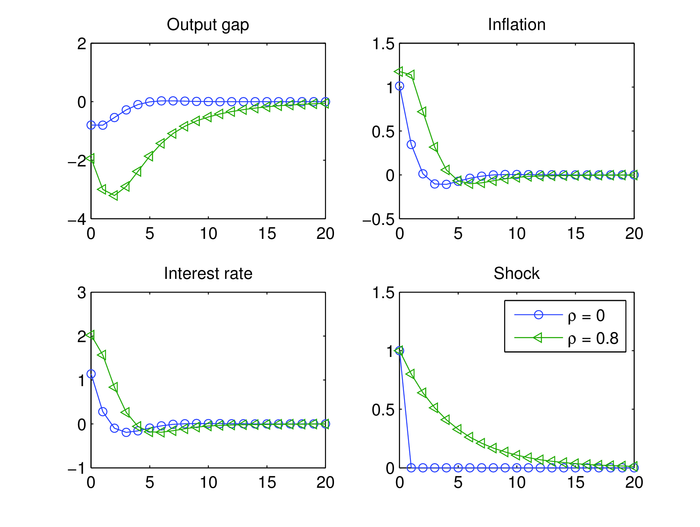
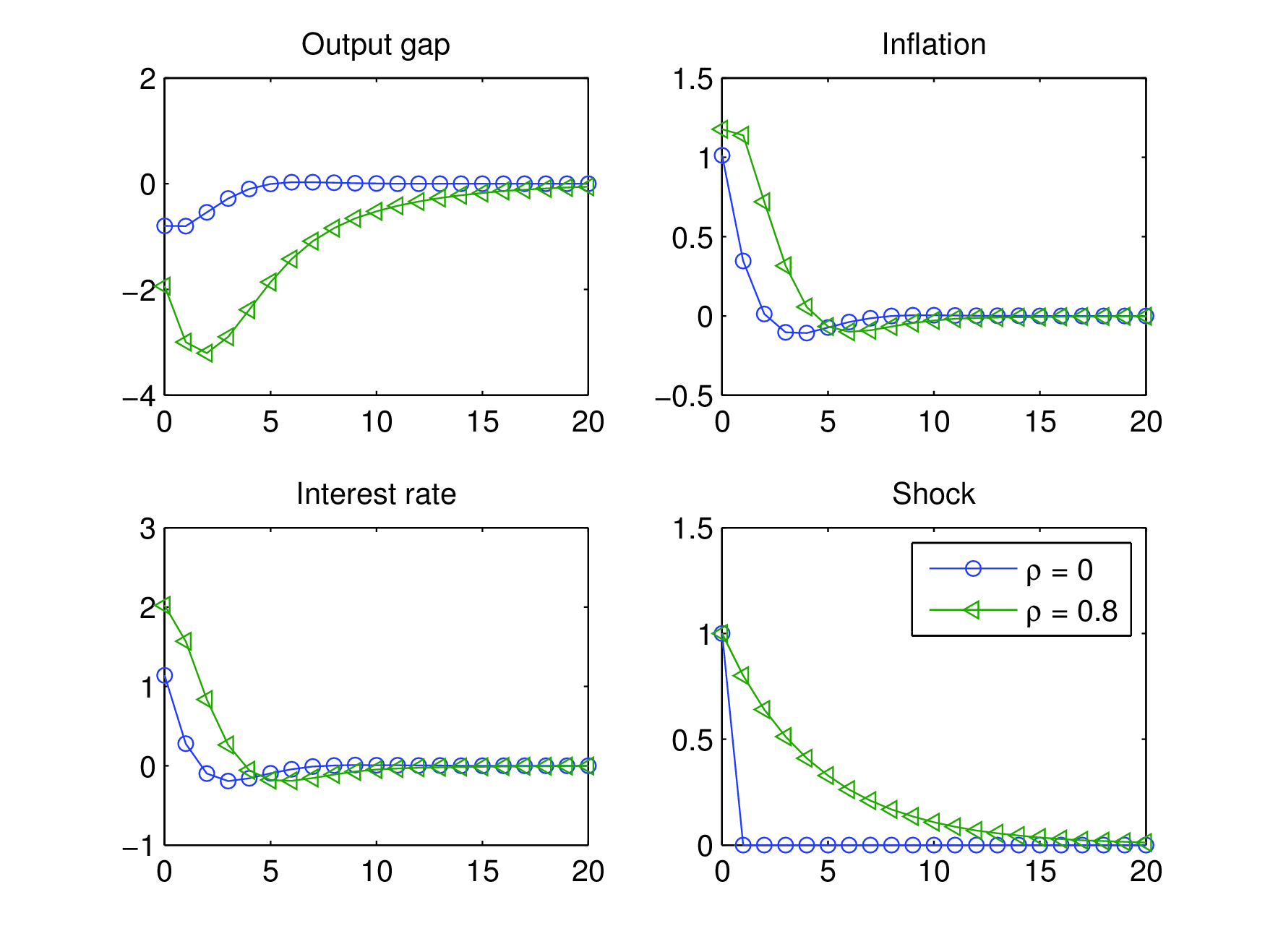
mit einem Glättungsparameter η, der zwischen null und eins liegt. Durch eine solche vergangenheitsorientierte Zinsregel vom Taylor-Typ wird ebenfalls Persistenz im rein vorausschauenden NKM-Grundmodell erzeugt, wenn ein One-off-Kostenschock vorliegt. Die modifizierte Taylor-Regel (10) stellt eine optimale einfache Regel (optimal simple rule (OSR)) dar, wenn die Bestimmung der Koeffizienten η, δ_π und δ_x über die Minimierung der Verlustfunktion (1) unter Beachtung der Gleichungen des NKM-Modells (IS-Gleichung, Phillips-Kurve und Taylor-Regel (10)) erfolgt. Eine derartige optimal simple rule mit smoothing liefert nahezu den gleichen  Verlust  wie unter der optimalen unrestringierten Geldpolitik und generiert Verläufe in den modellendogenen Variablen, die genau denen im Fall der optimalen unrestringierten Geldpolitik entsprechen (vgl. Abbildung „Kostenschock ohne Persistenz und optimale enfache Regel mit und ohne Glättung“). Ohne Zinsglättung (η = 0) würden sich wieder zweiperiodige Anpassungsprozesse wie im Grundmodell bei Vorliegen von Kostenschocks ohne Persistenz ergeben (Neukeynesianische Makroökonomik, dynamisches Grundmodell).

Bild in Originalgröße zeigen

„Kostenschock ohne Persistenz und optimale enfache Regel mit und ohne Glättung“

3. Optimale Geldpolitik im Hybrid-Fall: Die Eigenschaft der history dependence der optimalen targeting rule ist zu modifizieren, wenn zur hybriden Phillips-Kurve (hybride Systeme)

mit 0 < θ_f , θ_b < 1, θ_f + θ_b = 1

übergegangen wird. Stellt man dann – unter Beibehaltung der Verlustfunktion (1) - die FOC für ein Verlustminimum unter timeless perspective commitment auf und fasst diese zu einer Gleichung zusammen, ergibt sich die Zielregel

Diese ist im Fall θ_b > 0, d.h. bei Vorliegen einer hybriden Phillips-Kurve, nicht nur zurückblickend (d.h. von x_t-1 abhängig), sondern auch vorausschauend (d.h. von E_t x_t+1 abhängig). Dabei nimmt der vorausschauende Grad der Zielregel zu, je stärker zurückblickend die privaten Wirtschaftssubjekte sind (d.h. je größer der Parameter θ_b ausfällt). Im Grenzfall θ_b = 1, in welchem die Phillips-Kurve vollständig zurückblickend ist, ist die targeting rule nicht mehr von x_t-1 abhängig, sondern nur noch eine Funktion von x_t und E_t x_t+1. Demzufolge sind in optimal simple rules vom Taylor-Typ auch vorausschauende Elemente (wie E_t π_t+1 und E_t x_t+1) zu berücksichtigen, um dem minimalen Verlustindex, der sich im Regime der unrestringierten Geldpolitik unter Commitment ergibt, möglichst nahe zu kommen. Im Sonderfall einer vollständig zurückblickenden Phillips-Kurve könnten Taylor-Regeln mit smoothing vom Typ (10) sogar zu einer Destabilisierung des Systems (starken Zunahme der Inflations- und Outputvarianz) führen und dann nicht mehr wie ein eingebauter Stabilisator wirken.

4. Optimale diskretionäre Politik: Eine Alternative zur optimalen unrestringierten Politik unter Commitment, die allerdings mit deutlich höheren Verlustindizes verbunden ist, stellt das Regime der diskretionären Geldpolitik (Discretion) dar, bei welcher die Zentralbank in einem Prozess der sequenziellen Optimierung in jeder Periode ihre optimale geldpolitische Reaktion auf Schocks neu bestimmt (Geldpolitik). Dies hat die Konsequenz, dass im Gegensatz zum Regime Commitment die privaten Inflationserwartungen nicht mehr durch die Politik der Zentralbank beeinflussbar sind und bei der Festlegung der optimalen diskretionären Geldpolitik eine Datenvariable darstellen. In diesem Fall ist unter der rein vorausschauenden Phillips-Kurve (2) die Inflationserwartung E_t π_t+1 eine für die Zentralbank gegebene Größe. Die FOC unter Commitment (5) ist dann durch die Bedingung

zu ersetzen, sodass sich zusammen mit der unveränderten FOC (4) die targeting rule im Regime Discretion

ergibt. Die optimale Geldpolitik im Regime Discretion ist dadurch gekennzeichnet, dass die Inflationslücke nicht mehr von der Änderung Δx_t der Outputlücke abhängig ist (wie unter Commitment bei rein vorausschauender Phillips-Kurve), sondern von ihrem Niveau x_t, wodurch die history dependence der targeting rule verloren geht. Dadurch ergeben sich Anpassungsprozesse, die ebenso wie im Fall der Standard-Zinsregel (8) keine Persistenz und intrinsische Dynamik mehr aufweisen, wenn ein One-off-Kostenschock vorliegt. Folgt der Kostenschock einem autoregressiven Prozess erster Ordnung, ergeben sich ebenfalls im Vergleich zur Standard-Taylorregel analoge Impuls-Antwort-Folgen (vgl. Neukeynesianische Makroökonomik, dynamisches Grundmodell). Insbesondere bleibt dann die Inflationslücke während der gesamten Anpassung positiv, sodass unter Discretion im Gegensatz zum Regime Commitment keine langfristige Stabilisierung des Preisniveaus auf seinem Anfangsniveau erfolgt. Vielmehr ergibt sich als Folge des temporären Kostenschocks eine dauerhafte Steigerung des Preisniveaus, sodass sich durch den Übergang von Commitment zu Discretion ein stabilization bias einstellt. Wird eine hybride Phillips-Kurve der Art (12) zugrunde gelegt, erhält man unter Discretion wiederum eine von x_t-1 unabhängige targeting rule, die im Vergleich zum Regime Commitment noch stärker vorausschauend ist. Auch im Hybrid-Fall erhöht sich der Verlust durch den Wechsel von Commitment zu Discretion deutlich. Nur im Sonderfall θ_b = 1, d.h. einer vollständig zurückblickenden Phillips-Kurve, sind die Regime Commitment und Discretion äquivalent, d.h. liefern die gleiche targeting rule und den gleichen Verlustindex. Die Zielregel im Fall θ_b = 1 folgt dabei aus (12) und ist durch die Gleichung

gegeben. 

Vgl. zugehöriger Schwerpunktbeitrag Neukeynesianische Makroökonomik.