Neukeynesianisches Grundmodell mit begrenzter Rationalität
Übersicht
zuletzt besuchte Definitionen...
1. Charakterisierung: Ausgangspunkt des neukeynesianischen Grundmodells mit begrenzter Rationalität ist das dynamische Grundmodell der NKM (Neukeynesianische Makroökonomik, dynamisches Grundmodell). Die in der neukeynesianischen IS- und Phillips-Kurven-Gleichung auftretenden rationalen Zukunftserwartungen (Erwartungen) Et xt+1 und Et πt+1 (mit Et = rationaler (statistischer) Erwartungsoperator, xt+1 = Outputlücke der Periode t+1, πt+1 = Inflationsrate der Periode t+1) werden im NKM-Modell mit begrenzter Rationalität durch einfache Erwartungshypothesen autoregressiver Bauart (in Form stationärer, statischer und extrapolativer Erwartungen) ersetzt. Dabei werden (in Bezug auf die Erwartungsbildung) heterogene Agenten unterstellt. Diese haben grundsätzlich die Möglichkeit, unter den verschiedenen zurückblickenden Erwartungsmechanismen zu wählen und – in Abhängigkeit der von ihnen beobachteten Prognosequalität (Attraktivität) – die bisher verwendete Erwartungshypothese durch eine andere autoregressive Erwartungsheuristik zu ersetzen. Dadurch wird im NKM-Modell eine neuartige (Wechsel-)Dynamik (Switching Dynamics) erzeugt, die zusammen mit den zurückblickenden Erwartungen für eine erhöhte Persistenz und Volatilität der modellendogenen Variablen sorgt.
2. Modellgleichungen: Es gelten weiterhin die Modellgleichungen des dynamischen neukeynesianischen Grundmodells (Neukeynesianische Makroökonomik, dynamisches Grundmodell) mit dem einzigen Unterschied, dass anstelle des statistischen (rationalen) Erwartungsoperators Et zu subjektiven (heuristischen) Erwartungen Ẽt übergegangen wird. Mit der Notation wie im dynamischen NKM-Grundmodell ergibt sich dann das Gleichungssystem
Für die Störterme ut, kt und νt wird vereinfachend angenommen, dass sie normalverteilt mit Erwartungswert null und konstanter Standardabweichung σu, σk und σν sind und einem White-Noise-Prozess (weißes Rauschen) folgen. Es wird also keine Autoregression bzgl. der Störgrößen unterstellt. Für die subjektiv gebildete Erwartung Ẽt wird in Analogie zur Theorie agenten-basierter Finanzmärkte (Finanzmarkttheoretische Ansätze) angenommen, dass die Agenten (Unternehmen, Haushalte) aus einer Menge einfacher Heuristiken wählen können. Bzgl. der für die Folgeperiode t+1 erwarteten Inflationsrate rechnet ein (variabler) Teil der Agenten damit, dass sich die angestrebte stationäre Zielinflationsrate (Target Level) der Zentralbank π* einstellen wird (Target- oder stationäre Erwartungen Ẽttar), während ein weiterer Anteil mit der Inflationsrate der Vorperiode (πt-1) rechnet (was statischen Erwartungen Ẽtsta entspricht). Außerdem sind extrapolative Inflationserwartungen Ẽtext möglich, bei denen entweder eine Weiterentwicklung des in der jüngsten Vergangenheit beobachteten Trends erwartet wird (απ > 0) oder aber mit einer Umkehr des Trends gerechnet wird (απ < 0):
Analoge Erwartungen können bzgl. der Outputlücke in t+1 (xt+1) unterstellt werden:
Dabei steht x̅ für den Steady-State der Outputlücke. Der Koeffizient απ (αx) misst in (6) (bzw. (9)) die Stärke der Extrapolation. Im Sonderfall απ=0 (αx=0) wird für die Folgeperiode mit dem Wert der laufenden Periode (πt bzw. xt) gerechnet. Im Unterschied zu rationalen (modellkonsistenten) Erwartungen sind die einfachen Erwartungsheuristiken zwar mit systematischen Erwartungsirrtümern verbunden und in gewisser Weise auch beliebig, dafür haben sie den großen Vorteil, dass sie intuitiv und realistisch sind (weil sie – im Unterschied zu rationalen Erwartungen – von einem unvollständigen Informationsstand ausgehen und auch das wahre ökonomische Modell nicht mehr bekannt sein muss) und außerdem mittels Experimentalstudien überprüft werden können. Sie werden neuerdings auch als begrenzt-rationale Erwartungen (BRE) bezeichnet, weil die kognitiven Fähigkeiten der Wirtschaftssubjekte begrenzt sind und aufgrund von Informationskosten immer nur ein unvollständiger Informationsstand für die Prognosebildung herangezogen werden kann. Es ist daher vollkommen rational, einfache Heuristiken für die Bildung von Erwartungen zu verwenden. Begrenzt-rationale Erwartungen sind so gesehen nicht mit irrationalen Erwartungen gleichzusetzen. Eine grundlegende Eigenschaft des NKM-Modells mit begrenzter Rationalität besteht darin, dass die Wirtschaftssubjekte zwischen den verschiedenen Erwartungsheuristiken bzgl. Inflationsrate bzw. Outputlücke wechseln können. Dabei müssen die von einem Wirtschaftssubjekt angewandten Erwartungshypothesen für Ẽt πt+1 und Ẽt xt+1 nicht identisch sein. Grundlage für die Wahl einer bestimmten Heuristik ist die vergangene und beobachtbare Prognosequalität aller Erwartungsmechanismen. Basierend auf dem Erwartungsfehler
wird als Auswahlkriterium die zu einer Heuristik gehörige Attraktivität Atj, j=tar, sta, ext, die sich aus dem quadrierten Erwartungsfehler der Vorperiode t-1 und dem Attraktivitätsverlust der Periode t-1 zusammensetzt, zugrundegelegt:
Dabei misst der Memory-Parameter ζ mit 0 ≤ ζ ≤ 1 das Gedächtnis der Wirtschaftssubjekte bei der Attraktivitätswahl, wodurch das Attraktivitätsniveau im Fall 0< ζ <1 von allen vergangenen Fehlern mit einer Gewichtungsstruktur, die einer abnehmenden geometrischen Reihe folgt, abhängt:
(mit j=tar, sta, ext; y=π, x und dem Ausgangswert A0j=0).
Da die Attraktivität einer Heuristik j in negativer Wise von den quadratischen Erwartungsfehlern der Vergangenheit abhängig ist, ist sie umso unattraktiver (stärker negativ), je größer diese Fehler sind. Im Sonderfall eines Memory-Parameters in Höhe von null hat nur der Erwartungsfehler der Vorperiode t-1 Einfluss auf die Attraktivität; weiter zurückliegende Fehler werden dann „vergessen“ (nicht berücksichtigt). Im anderen Grenzfall ζ=1 wird kein Fehler aus der Vergangenheit jemals vergessen und geht stets mit dem gleichen Gewicht eins in die Berechnung des Attraktivitätsniveaus ein. Wird der Regelfall 0< ζ <1 angenommen, haben weiter in der Vergangenheit liegende Fehler einen geringeren Einfluss auf die Attraktivität als die Fehler der jüngsten Vergangenheit. Mithilfe eines Discrete-Choice-Ansatzes (Discrete-Choice-Theory) lässt sich aus der Gesamtmenge aller Wirtschaftssubjekte genau derjenige Anteil (fraction) ωtj(y) ermitteln, der in Periode t eine bestimmte Erwartungsheuristik j zur Prognosebildung von yt+1 anwendet:
(mit j=tar, sta, ext und y=π, x). Dabei steht exp(·) für die Exponentialfunktion und Φ für den nichtnegativen Rationalitäts-oder Intensity-of-Choice-Parameter, welcher den Grad der „Rationalität“ der Wirtschaftssubjekte misst. Im Falle Φ=0 ergibt sich eine rein zufällige Wahl der Heuristik j; dabei sind die zugehörigen Anteile stets identisch und gleich ⅓:
Im anderen Extremfall Φ → ∞ wählen alle Agenten die gleiche Heuristik, und zwar die mit der höchsten Attraktivität (dem betragsmäßig kleinsten Attraktivitätsniveau). Generell gilt, dass für 0< Φ < ∞ die Anteile ωtj in der Zeit variieren und eine Wechseldynamik (Switching Dynamics) erzeugen. Dabei sind die Anteile in positiver Weise von der Attraktivität Atj abhängig. Je kleiner die in der Vergangenheit beobachteten Erwartungsfehler einer Heuristik j sind, desto größer ist ihre Attraktivität und desto größer ist der Anteil der Agenten, die diese Erwartungsheuristik für die Prognosebildung verwenden. Die Anteile aller Heuristiken müssen sich dabei stets zum Wert eins aufaddieren:
Die Markterwartung oder gesamtwirtschaftliche Erwartung Ẽt(yt+1) für die Inflationsrate bzw. Outputlücke in t+1 ergibt sich als gewichtete Summe der Einzelerwartungen Ẽtj(yt+1) mit den zugehörigen Anteilen ωtj(y) als Gewichte:
Je attraktiver eine Erwartungsheuristik Ẽtj(yt+1), desto mehr Agenten werden sie wählen, sodass der zugehörige Anteil ωtj(y) steigt und damit auch ihr Einfluss auf die Markterwartung. Im Unterschied zur rationalen Inflations- bzw. Outputlückenerwartung Etπt+1 bzw. Etxt+1 ist die begrenzt-rationale Erwartung Ẽtj(πt+1) bzw. Ẽtj(xt+1) nicht mehr vorausschauend, sondern von laufenden, vergangenen und exogenen Variablen, d.h. πt, πt-1 sowie dem Target Level π* bzw. xt, xt-1 und dem Steady-State-Niveau x̅ abhängig. Die zugehörigen Koeffizienten in den Zustandsgleichungen sind außerdem aufgrund der unterstellten Wechselmöglichkeit der gewählten Erwartungsheuristik zeitabhängig.
3. Dynamik des Modells: Die Dynamik des NKM-Modells mit begrenzt-rationalen Erwartungen lässt sich mithilfe der Zustandsgleichungen des Systems generieren. Analog zum dynamischen neukeynesianischen Grundmodell (Neukeynesianische Makroökonomik, dynamisches Grundmodell) wird dazu die IS-Gleichung (1) mit der Zinsregel (2) kombiniert, woraus die aggregierte Nachfragekurve resultiert. Zusammen mit der Phillips-Kurven-Gleichung (3) ergibt sich dann ein zweidimensionales dynamisches System in den Zustandsvariablen πt und xt, in welchem noch die Markterwartungen Ẽt(πt+1) und Ẽt(xt+1) durch die Definitionsgleichung (16) unter Berücksichtigung der Erwartungsheuristiken (4)-(9) zu ersetzen sind. Es gelten dann für πt und xt die Systemgleichungen
mit den Markterwartungen
Für numerische Simulationen werden die Konstanten i*, π* und x̅ auf den Wert null normiert (i*=π*= x̅=0), sodass aus (17)-(20) die Matrixform
mit den zeitabhängigen Systemmatrizen
und
resultiert. Durch Auflösen nach dem laufenden Zustandsvektor (πt, xt) ergeben sich dann die Zustandsgleichungen des NKM-Modells mit begrenzt-rationalen Erwartungen:
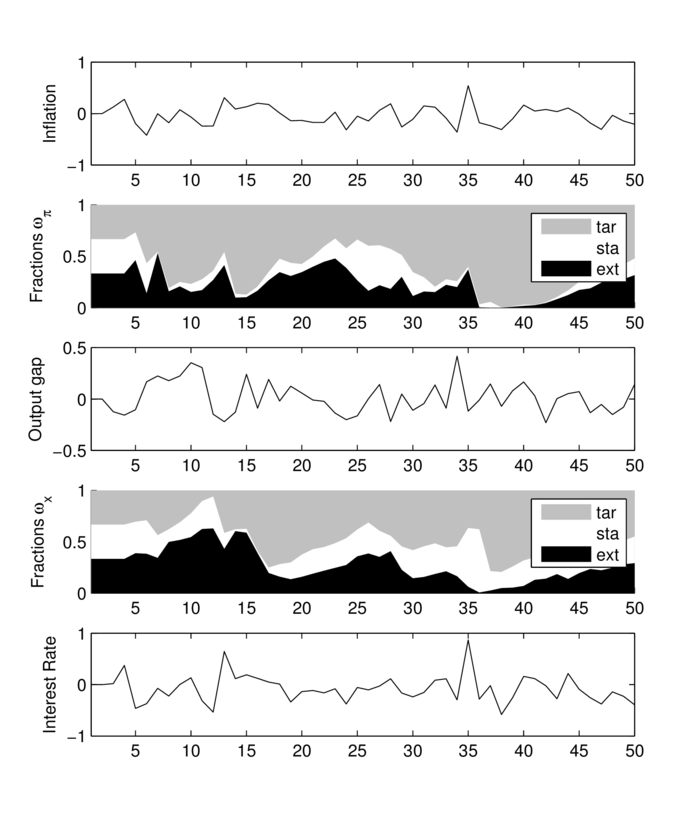
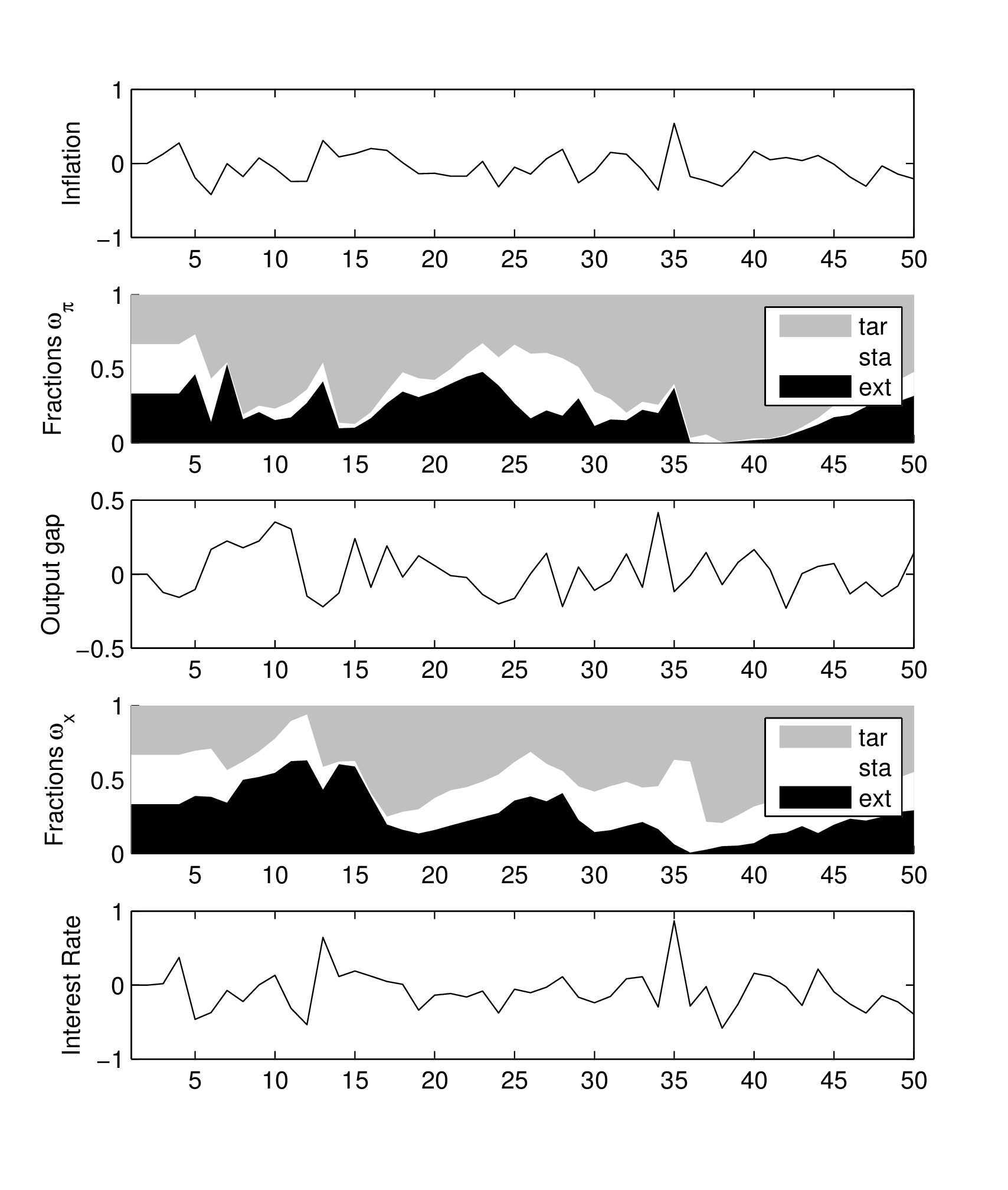
Diese beschreiben vollständig die Dynamik des neukeynesianischen Grundmodells, wenn von rationalen zu begrenzt-rationalen Erwartungen mit der Möglichkeit des Wechselns der Erwartungsheuristik übergegangen wird. Es ergibt sich dann anstelle eines vorausschauenden ein zurückblickendes dynamisches System mit zeitabhängigen Koeffizienten, das numerisch mithilfe eines geeigneten Computer-Algorithmus gelöst werden kann. Abbildung „NKM-Modell unter begrenzt-rationalen Erwartungen“ zeigt beispielhaft den Simulationsverlauf der Inflationsrate πt, der Outputlücke (output gap) xt und des Nominalzinssatzes (interest rate) it. Außerdem enthält
Abbildung „NKM-Modell unter begrenzt-rationalen Erwartungen"
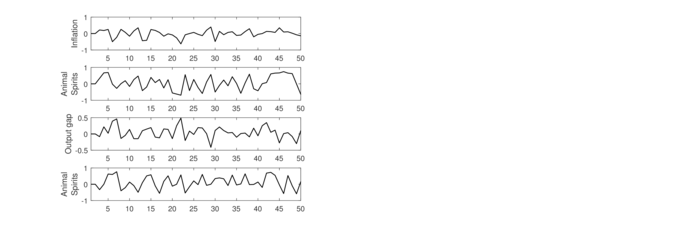
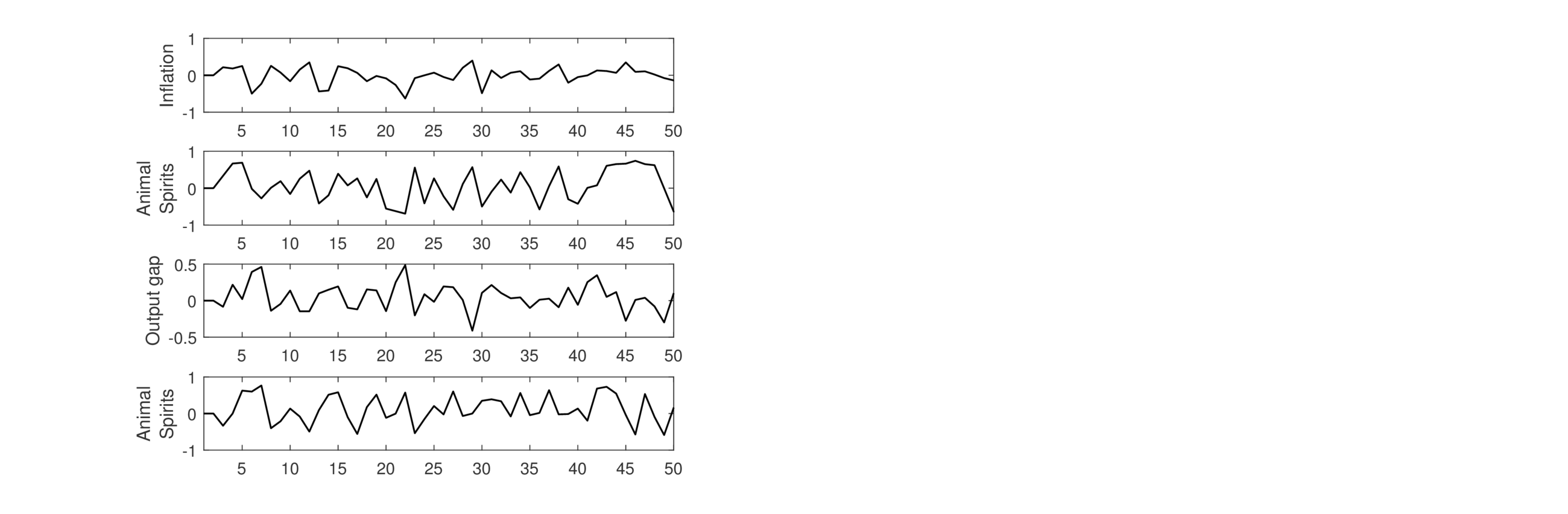
die Abbildung die zeitliche Entwicklung der Anteile (fractions) ωtj(π) und ωtj(x) (j=tar, sta, ext). Dem dargestellten simulierten Verlauf der Variablen über 50 Perioden liegt eine konkrete Realisation der Störgrößen νt, ut und kt zugrunde. Diese werden im Algorithmus als Pseudo-Zufallszahlen aufgefasst (die durch einen Zufallszahlengenerator mit seed initialisiert werden), sodass die Verläufe von πt, xt und it stochastisch sind. Sie stellen nur einen unter einer Vielzahl möglicher Verläufe dar. Würde man eine große Zahl unterschiedlicher Simulationen durchführen und dann daraus den mittleren Verlauf von πt, xt und it bestimmen (indem in jeder Periode t der zugehörige Mittelwert berechnet wird), ergäbe sich aufgrund der unterstellten Normalverteilungshypothese für die Störgrößen für jede der drei Variablen πt, xt und it der Wert null für jede Periode t. Der mittlere Verlauf der modellendogenen Variablen ist dann gleich null, da sich positive und negative Realisationen der Störgrößen im Mittel genau aufheben. Weiter zeigen die Plots den Einfluss der (willkürlich gewählten) Startbedingungen für den Verlauf von πt, xt und it. Die Inflationsrate πt liegt zunächst (d.h. für t=1 und t=2) beim Steady-State-Wert in Höhe von null. Für die zugehörigen Erwartungsheuristiken Ẽtj(πt+1), j = tar, sta, ext, liegen zu Beginn des Simulationslaufs noch keine (negativen) Attraktivitätswerte vor, sodass sich die Anteile ωtj(π) zunächst für einige Zeit in der Nähe von ⅓ befinden. Ein Lernverhalten der privaten Wirtschaftssubjekte setzt erst im Laufe der Zeit ein, da sie zunächst einige Realisationen von πt (und entsprechend auch xt und it) beobachten müssen, um ihre Erwartungsfehler und das daraus resultierende Attraktivitätsniveau zu berechnen und aus den Fehlern zu lernen. Für hinreichend großes t (ab der Periode t=11) kann man davon ausgehen, dass der Lernprozess so weit fortgeschritten ist, dass der Einfluss der (willkürlichen) Startbedingungen auf die weitere Entwicklung von πt, xt und it zu vernachlässigen ist. Diese sog. Burn-in-Phase ist im Grunde bei allen Simulationsläufen „abzuschneiden“ (zu vernachlässigen), sodass in der Abbildung „NKM-Modell unter begrenzt-rationalen Erwartungen“ von einer faktischen Simulationslänge von 40 Perioden auszugehen ist. Für die Entwicklung der Anteile ωtj(π) gilt, dass die Gruppe der Targeters, die sich bei ihrer Inflationserwartungshypothese am Target Level π*(=0) der Zentralbank ausrichtet, immer dann dominiert, wenn die Inflationsrate in der Nähe des Nullniveaus liegt. Ist dagegen ein Trend in der Entwicklung von πt erkennbar, nimmt der Einfluss der Extrapolierer und der Agenten mit statischen Erwartungen zu. Generell zeigt die Entwicklung der Anteile ωtj eine hohe Wechseldynamik (Switching Dynamics), die auch dafür verantwortlich ist, dass sich die Volatilität der modellendogenen Variablen durch den Übergang von rationalen zu begrenzt-rationalen Erwartungen erhöht. Ein weiterer Anspekt ist, dass sich die auf Keynes zurückgehenden Animal Spirits (d.h. der Wechsel von optimistischen zu pessimistischen Stimmungen (Erwartungen)) modelltheoretisch mithilfe heuristischer Erwartungsmechanismen erfassen lässt. Von optimistischen (pessimistischen) Erwartungen würde man – bezogen auf die Outputlücke x und die Inflationsrate π – dann sprechen, wenn unter der gewählten Erwartungsheuristik Ẽtj(yt+1) für die Folgeperiode t+1 mit einer positiven (negativen) Outputlücke bzw. Inflationsrate gerechnet wird. Unter optimistischen Erwartungen wird also für die Periode t+1 unterstellt, dass das Outputniveau über seinem Potenzialoutput liegt und – bezogen auf die Inflationsrate – keine Deflation eintritt. Man kann im nächsten Schritt den Agenten mit optimistischen (pessimistischen) Erwartungen den Wert +1 (bzw. -1) zuordnen und den Agenten, die eine Rückkehr ins Target Level (bzw. den Steady-State) erwarten, den Wert null, und dann unter Animal Spirits die mit ihren Anteilen gewichtete Summe der drei Zustände +1, -1 und 0 verstehen. Dadurch ergibt sich eine Zeitreihe für die endogen erklärten Animal Spirits, die stark um die Nulllinie schwankt und den häufigen Wechsel von optimistischen zu pessimistischen Erwartungen erfasst (vgl. die Abbildung „Animal Spirits im NKM-Modell mit begrenzt-rationalen Erwartungen“). Die Dynamik, die aus dem Wechsel von Stimmungen resultiert, wird auch als Sentiment Dynamics bezeichnet. Für den Konjunkturverlauf können diese wie ein Akzelerator wirken, d.h. die positive (negative) Entwicklung in den Zustandsvariablen, die sich als Folge eines zufälligen expansiven (kontraktiven) Impulses ergibt, verstärken.
Abbildung „Animal Spirits im NKM-Modell mit begrenzt-rationalen Erwartungen“
Animal Spirits wirken dann wie eine sich selbst erfüllende Prophezeiung. Nimmt die Attraktivität von Erwartungsheuristiken mit optimistischen Erwartungen zu, erhöht sich der Anteil der Wirtschaftssubjekte, die für die Folgeperiode mit einer positiven Outputlücke bzw. Inflationsrate rechnen. Über die Markterwartungen wirkt sich dieses Verhalten positiv auf den laufenden Konsum und die Outputlücke sowie die Inflationsrate aus. In der Folgeperiode t+1 kann es dann zu einem weiteren Anstieg der Erwartungen und der Outputlücke sowie der Inflationsrate kommen. Diese Akzeleratorfunktion optimistischer (bzw. pessimistischer) Erwartungen weist starke Ähnlichkeit mit dem Herdenverhalten von Agenten auf den Finanzmärkten auf.
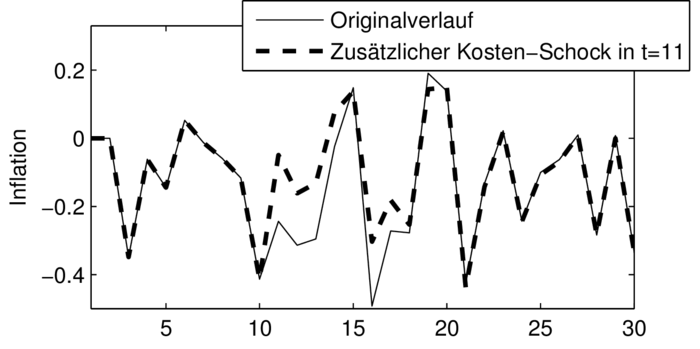
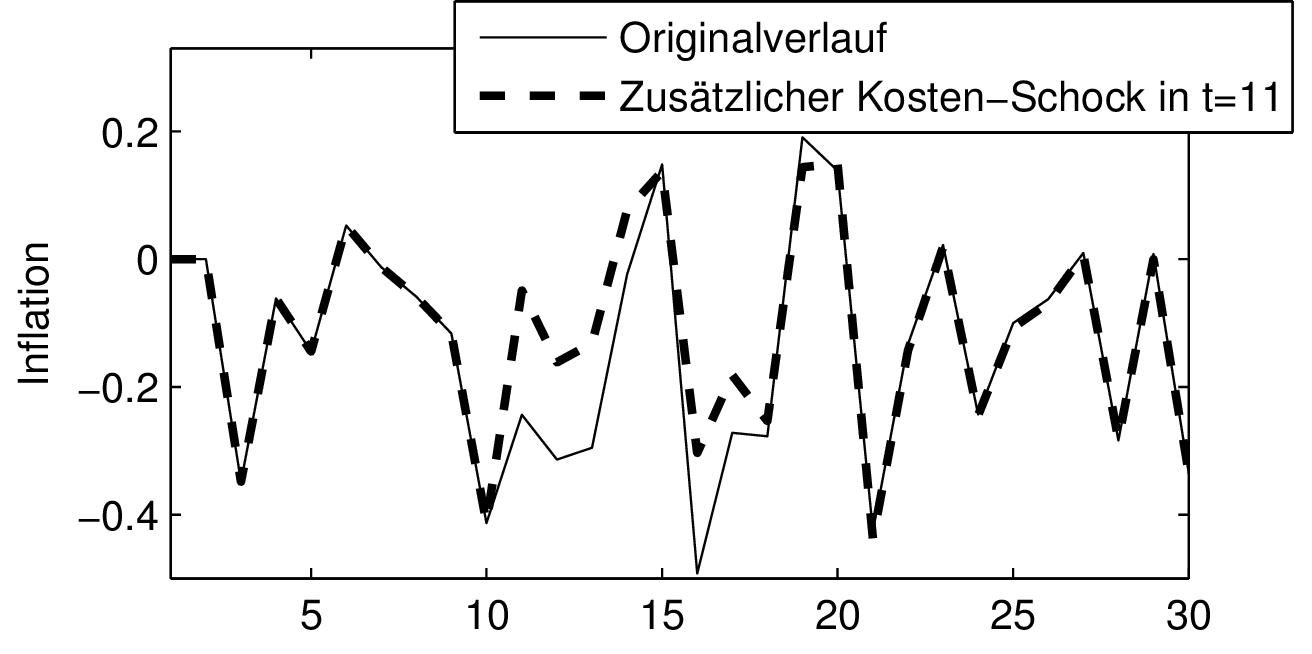
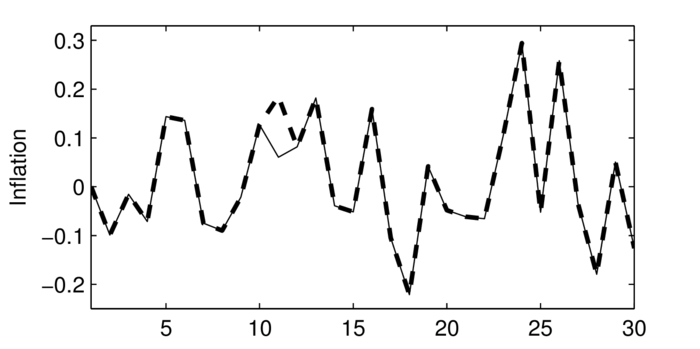
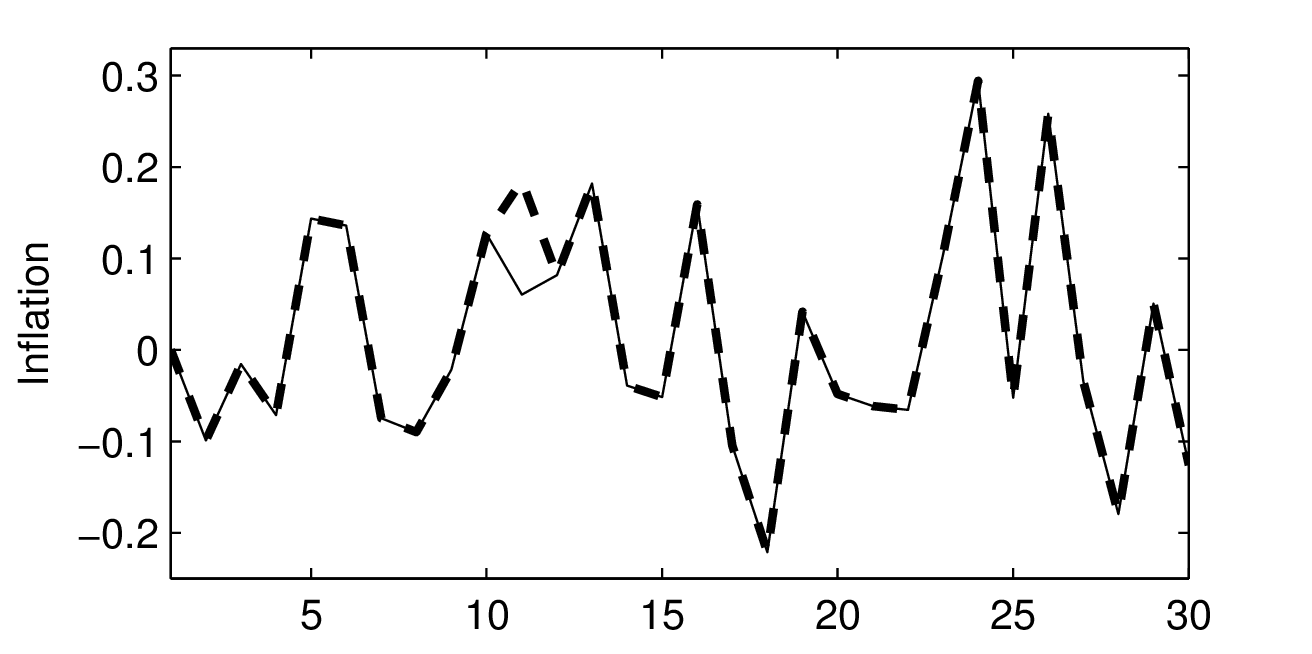
4. Impuls-Antwort-Folgen: Um die Modelldynamik des NKM-Modells unter begrenzt-rationaler Erwartungsbildung (BRE) mit der unter rationaler Erwartungsbildung (RE) zu vergleichen, wird den zufälligen stochastischen Impulsen ein zusätzlicher exogener Schock hinzugefügt. Und zwar wird unterstellt, dass im Anschluss an die Burn-in-Phase in Periode t=11 ein isolierter Kostenschock ohne Persistenz im Ausmaß seiner Standardabweichung σν auftritt. Die Auswirkungen des One-off-Schocks ν11= σν > 0 werden in der Abbildung „Inflationswirkungen einer exogenen Erhöhung der Störgröße ν11 unter BRE (links) und RE (rechts)“ veranschaulicht. Der ursprüngliche Simulationsverlauf wird durch die durchgezogene Linie dargestellt, während die gestrichelte Linie die Reaktion (Antwort) von πt unter BRE (links) und RE (rechts) zeigt, wenn zusätzlich in t=11 ein isolierter Kostenschock (Impuls) auftritt (Impuls-Antwort-Folgen). Unter BRE und RE sind die Inflationsverläufe bis zum Schockzeitpunkt jeweils identisch. In t=11 erhöht sich in beiden Fällen die Inflationsrate. Gleichzeitig würde die Outputlücke über den Anstieg des Realzinses sprunghaft zurückgehen. Da der Kostenschock keine Persistenz aufweist und unter rationalen Erwartungen ein rein vorausschauendes System vorliegt, beträgt die isolierte Wirkung dieses Schocks im RE-Fall lediglich zwei Perioden (vgl. Neukeynesianische Makroökonomik, dynamisches Grundmodell), sodass ab der Periode t=12 wieder der Originalverlauf von πt gilt. Im BRE-Fall liegt dagegen ein zurückblickendes System vor, das ähnlich wie ein hybrides NKM-Modell (hybride Systeme) eine längerfristige (persistente) Reaktion auch bei Vorliegen eines One-off-Schocks erzeugt, sodass sich in den Folgeperioden t=12,13,… weiterhin eine Abweichung vom ursprünglichen Verlauf ergibt. Im RE-Fall ist die Antwort des Impulses nur auf die Schockperiode begrenzt, während sie sich im BRE-Fall als Folge zurückblickender Erwartungen über eine Reihe von Perioden erstreckt und erst langfristig verschwindet. Außerdem hängt die Wirkung des Schocks auf den Verlauf des Systems für t≥11 im Fall begrenzt-rationaler Erwartungen vom Zustand des Systems im Schockzeitpunkt t=11 ab. Die quantitative Reaktion der modellendogenen Variablen auf den Kostenschock ist im BRE-Fall maßgeblich von der Ausgangs- bzw. Konjunkturlage in t=11 abhängig. Eine Volkswirtschaft, die sich im Schockzeitpunkt in einer Rezession befindet, reagiert unter begrenzt-rationalen Erwartungen anders auf einen Impuls als in der Boomphase. Um den
Abbildung „Inflationserwartungen einer exogenen Erhöhung der Störgröße ν11 unter BRE (links) und RE (rechts)“
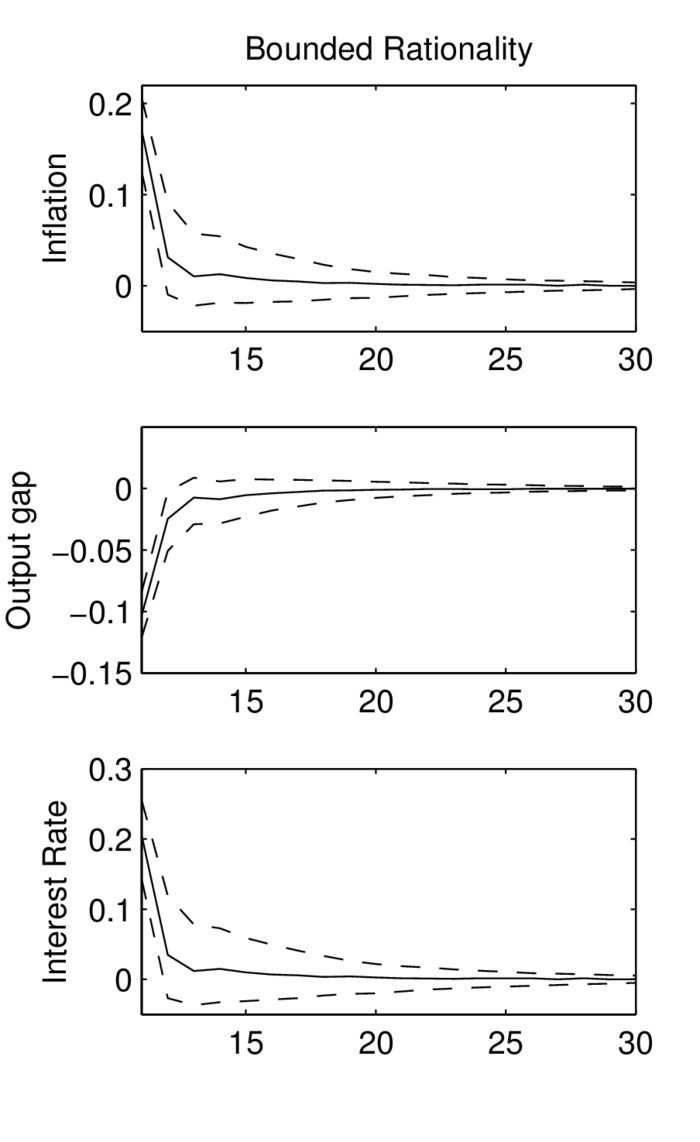
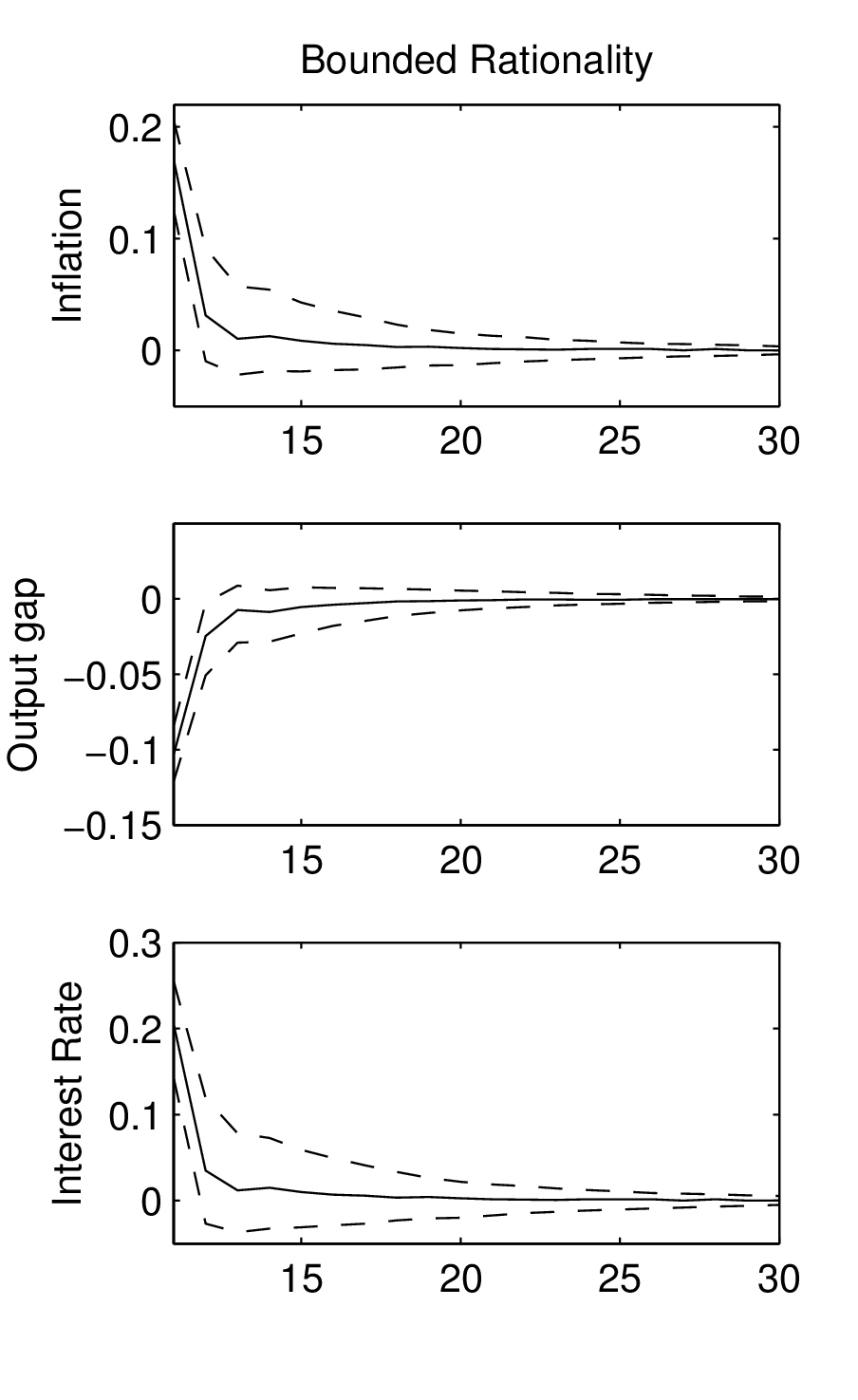
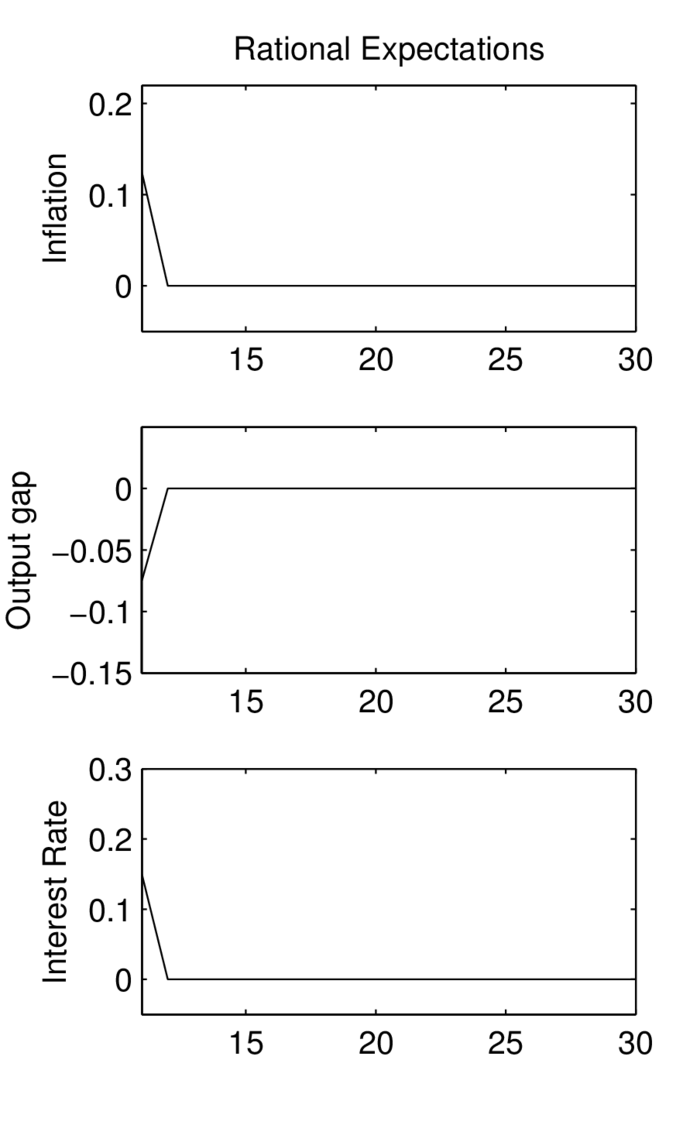
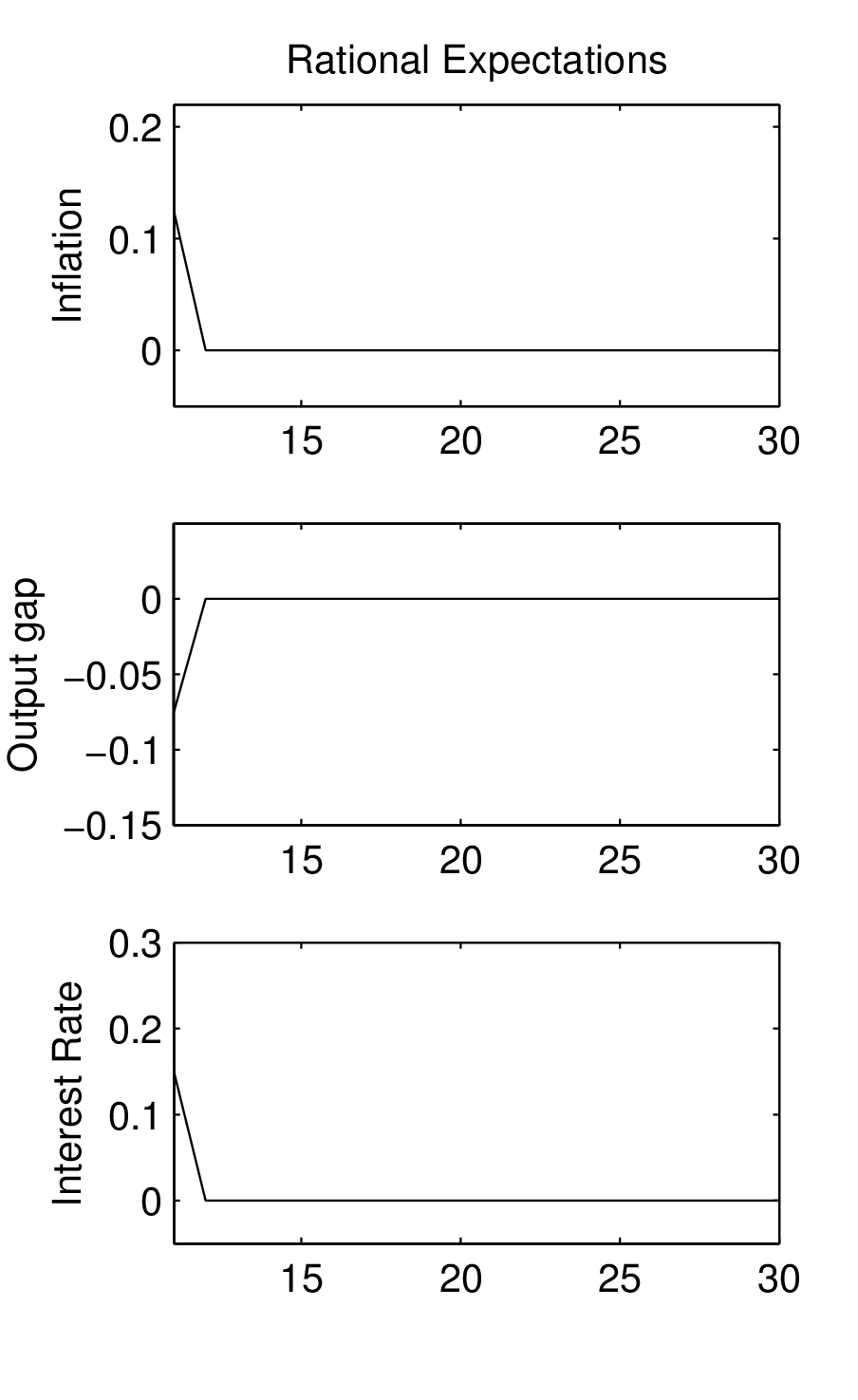
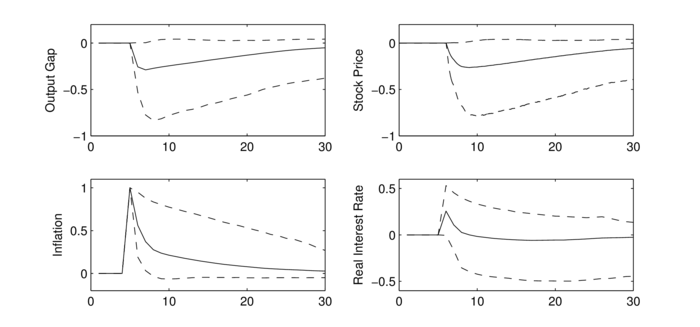
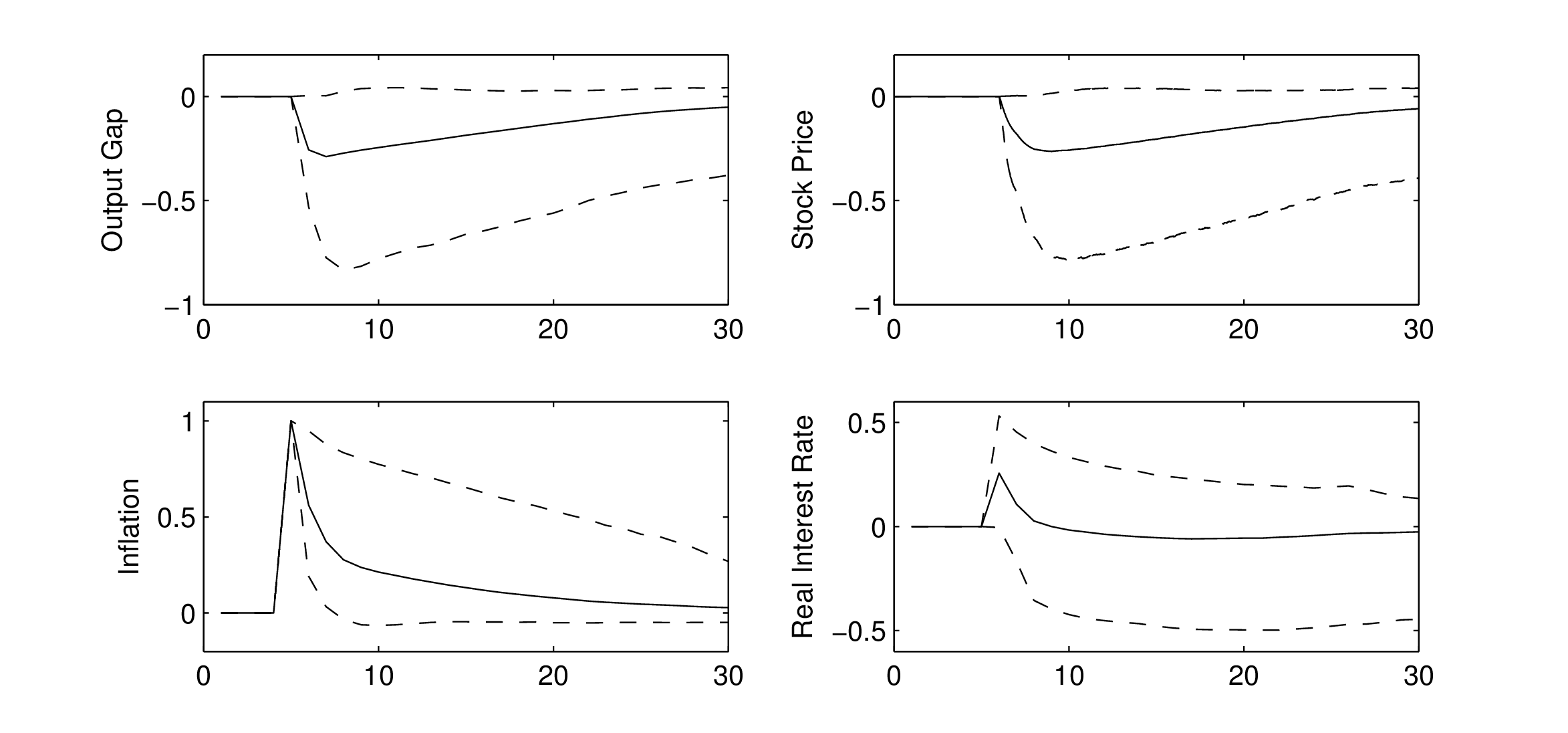
Einfluss des Ausgangszustandes der Ökonomie auf die Auswirkungen des Schocks zu vermeiden, kann man die Differenz der Inflationsverläufe mit und ohne zusätzlichen Kostenschock für zahlreiche Szenarien (seeds) simulieren und daraus den mittleren Inflationsverlauf berechnen. Entsprechend kann man mit der Outputlücke x und dem Nominalzins i verfahren. Es ergeben sich dann Impuls-Antwort-Folgen (Impulse Response Functions (IRF)), die in der Abbildung „Impuls-Antwort-Folgen eines Kostenschocks unter BRE (links) und RE (rechts)“ durch durchgezogene Linien veranschaulicht werden.
Abbildung „Impuls-Antwort-Folgen eines Kostenschocks unter BRE (links) und RE (rechts)“
Dabei wird der Zeitraum ab der Schockperiode t=11 betrachtet. Aus qualitativer Sicht ist die Reaktion des Systems unter BRE (Bounded Rationality) und RE (Rational Expectations) identisch (in beiden Fällen ergibt sich Stagflation, die mit einer Zinssteigerung verbunden ist). Im Unterschied zu rationalen Erwartungen sind die IRF unter BRE vom Zustand der Ökonomie im Schockzeitpunkt abhängig, welcher mit Unsicherheit behaftet ist. Dieser Unsicherheit wird durch Konfidenzbänder (gestrichelte Linien) in der Abbildung Rechnung getragen, innerhalb derer die Verläufe von πt, xt und it im Fall BRE mit 80%iger Wahrscheinlichkeit liegen. Dagegen ergeben sich unter RE keine Konfidenzbänder, da in diesem Fall die Reaktion des Systems immer identisch ist. Unter BRE dauert es eine Reihe von Perioden, bis die Wirkung des Kostenschocks vollkommen abgeklungen ist. Erst nach ca. 20 Perioden stellt sich ein sehr enges Konfidenzband ein, welches direkt am Mittelwert liegt. Im Fall rationaler Erwartungen ist dagegen die Wirkung des One-off-Schocks auf die modellendogenen Variablen auf die Schockperiode begrenzt. Bereits ab der Folgeperiode erfolgt die Rückkehr in den Anfangs-Steady-State (den Nullzustand). Im Fall begrenzt-rationaler Erwartungen kann die Reaktion der Variablen mit positiver Wahrscheinlichkeit sogar einem Vorzeichenwechsel unterliegen. Erkennbar ist dies an den unteren gestrichelten Linien, die verdeutlichen, dass nur wenige Perioden nach dem Schockeintritt negative Werte der Inflationsrate und des Zinssatzes auftreten können. Unter RE ist diese Möglichkeit dagegen ausgeschlossen.
5. Weiterentwicklungen: Das neukeynesianische Grundmodell mit begrenzt-rationalen Erwartungen lässt sich in mehrfacher Hinsicht weiterentwickeln: Berücksichtigung von rationalen Erwartungen, Erweiterung zu einem Macro-Finance-Dynamics-Modell, Übergang zu einem Agent-Based-Computational-Economics-Modell.
a) Grundsätzlich können im NKM-Modell mit heterogenen Erwartungen neben begrenzt-rationalen zusätzlich auch rationale Erwartungen berücksichtigt werden. Da die Bildung rationaler Erwartungen einen hohen Informationsstand erfordert und die Beschaffung und Verarbeitung prognoserelevanter Informationen mit Kosten verbunden ist, ist es naheliegend, in der zugehörigen Attraktivitätsgleichung vom Typ (11) Informations- oder Wechselkosten (switching costs) zu berücksichtigen:
Dabei sind cRE ≥ 0 konstante switching costs. Unter RE ist der Erwartungsfehler nur unsystematischer (zufallsabhängiger) Natur und im Mittel sogar gleich null. Durch die Berücksichtigung von Wechselkosten verliert diese Form der Erwartungsbildung allerdings an Attraktivität. Dies hat die Konsequenz, dass auch im langfristigen Gleichgewicht (Steady-State) die Attraktivität unter RE nicht auf den Wert null ansteigt (wie im Fall heuristischer Erwartungen, bei denen die Wechselkosten cj gleich null sind), sondern einen negativen Wert annimmt. Langfristig liegt dann keine Gleichverteilung der Anteile (d.h. ωj(y) = ¼ für j=tar, sta, ext, RE) vor; vielmehr dominieren dann die BRE. Auf der anderen Seite wirken RE aber stabilisierend, d.h. vermindern die Volatilität des Systems, da sie zu kleineren Varianzen der modellendogenen Variablen führen als unter BRE. Demzufolge nimmt die Volatilität des Systems zu, wenn die Wechselkosten cRE ansteigen. Für hinreichend hohe Werte von cRE geht der Anteil ωRE(y) sogar gegen null, sodass dann die Volatilität am größten ist. Numerische Simulationen zum BRE-Modell unter Berücksichtigung RE sind extrem zeitaufwendig (da für jeden Simulationslauf in jeder Periode ein statistischer Erwartungswert mittels numerischer Approximation zu berechnen ist) und in der Literatur kaum zu finden; gelegentlich begnügt man sich damit, mit der Extremform rationaler Erwartungen, d.h. mit perfekter Voraussicht, zu arbeiten. Dadurch werden unsystematische Fehler, die in einem stochastischen NKM-Modell auch unter RE auftreten, vernachlässigt, sodass sich die Attraktivität nur noch aus der Summe diskontierter switching costs zusammensetzt und im Sonderfall cRE = 0 stets den Wert null annimmt. Diese vereinfachende Vorgehensweise ist allerdings fragwürdig, da in stochastischen NKM-Modellen, die Varianten von DSGE-Modellen (dynamische stochastische allgemeine Gleichgewichtsmodelle) darstellen, rationale Erwartungen nicht mit perfekter Voraussicht gleichzusetzen sind.
b) Neukeynesianische Modelle bilden nur den realen Sektor einer Volkswirtschaft (Gütermarkt, Faktormärkte) ab; der monetäre Sektor (Geldmarkt, Kreditmarkt, Finanzmärkte) bleibt dagegen unberücksichtigt. Angesichts der jüngsten Finanzkrise 2007/2008 (Subprime-Krise) und die damit verbundene weltweite Tiefenrezession 2009 ist es naheliegend, finanzmarkttheoretische Ansätze in das NKM-Modell zu integrieren, also zu einer Macro-Finance-Dynamics überzugehen. Die Theorie künstlicher Finanzmärkte (finanzmarkttheoretische Ansätze) ist -bezogen auf den Aktienmarkt (stock market)- durch heterogene Agenten (Chartisten, Fundamentalisten) und heterogene Erwartungen bzgl. des zukünftigen Aktienpreises (stock price) gekennzeichnet. Während Chartisten extrapolative Erwartungen bilden und von einer Fortsetzung der jüngsten Stock-Price-Entwicklung ausgehen, unterstellen Fundamentalisten eine Rückkehr zum Fundamentalpreis. Für beide Akteure lässt sich dann die jeweilige Überschussnachfrage nach stocks in proportionaler Abhängigkeit der erwarteten Änderung des Aktienpreises definieren und darauf aufbauend die Attraktivität der Handelsstrategie der Chartisten bzw. Fundamentalisten in Abhängigkeit des damit erzielten vergangenen Profits festlegen. Außerdem können noch als weitere Agenten die passiven, die keine trading strategy verfolgen, berücksichtigt werden. Es können dann durch Anwendung der Discrete-Choice-Theory entsprechend Gleichung (13) die mit der Zeit variierenden Anteile der Finanzmarktagenten ermittelt werden, sodass die mit diesen Anteilen gewichteten Überschussnachfragemengen die Stock-Price-Änderung auf dem Finanzmarkt festlegen. Es lassen sich dann – analog zum NKM-Modell unter BRE – switching dynamics bzgl. der Entwicklung der Anteile der Chartisten, Fundamentalisten und passiven Agenten auf dem Finanzmarkt erzeugen. In einem weiteren Schritt ist das Finanzmarktmodell mit dem NKM-Modell durch Übertragungskanäle zu verknüpfen. So lässt sich in der Phillips-Kurve der Aktienpreis mit einem negativen Gewicht berücksichtigen, da mit steigendem Preis auch die unternehmerische Bonität zunimmt und Kredite dann mit geringeren Zinskosten verbunden sind, was sich wiederum dämpfend auf die Stückkosten auswirkt. Der Kostenkanal stellt dann einen Interaktionskanal zwischen Finanz- und Realmarkt dar. Auch in der IS-Kurve lässt sich der stock price als Verbindungskanal mit aufnehmen, und zwar in Form seiner erwarteten realen Änderungsrate, was sich mikrotheoretisch begründen lässt, indem man analog zur Realkassenhaltung unterstellt, dass die privaten Haushalte auch Aktien in ihrem Portfolio halten und somit die Nachfrage nach stocks nutzenstiftend ist und über eine nicht-separable Nutzenfunktion den Grenznutzen des Konsums steigert. Dann erhöht eine erwartete Zunahme des realen stock price den laufenden Konsum (weil dann der zukünftig erwartete Konsumgrenznutzen zurückgeht) (vgl. Euler-Gleichung des Konsums) und dann auch den Output und die Outputlücke. Eine weitere Interaktion zwischen Finanzmarkt und Gütermarkt tritt auf, wenn der Fundamentalwert des Aktienpreises, der Grundlage für die Kaufentscheidung der Fundamentalisten ist, an die Outputlücke (als Maß für das Wirtschaftswachstum) gekoppelt ist. Außerdem fragen auch die privaten Haushalte (neben den institutionellen Anlegern in Form von Fundamentalisten und Chartisten) Aktien nach (da diese nutzenstiftend sind), sodass in der aggregierten Nachfrage nach stocks auch die Nachfrage der Haushalte zu berücksichtigen ist, welche dann zusammen mit der Nachfrage der institutionellen Anleger die Stock-Price-Änderung determiniert. Insgesamt lassen sich dann vier Interaktionskanäle identifizieren. Schließlich ist noch in einem Macro-Finance-Dynamics-Modell zu berücksichtigen, dass einem isolierten Simulationslauf eines NKM-Modells mit BRE eine andere Zeitskala zugrunde liegt als einem entsprechenden Lauf eines Finanzmarktmodells, da die Handelsfrequenz auf Finanzmärkten deutlich höher ist als auf Gütermärkten. Empirisch gesehen sind Finanzmarktdaten täglich verfügbar, während für Realmarktdaten eine Quartalsbetrachtungsweise gilt. Üblicherweise wird in integrierten Finanzmarkt-Realmarkt-Modellen angenommen, dass ein Quartal aus 64 Tagen (in denen Finanzmarkttransaktionen getätigt werden) besteht und sich der in der IS-Gleichung und Phillips-Kurve auftretende Quartalswert des Aktienpreises als Durchschnitt der zugehörigen 64 Tageswerte zusammensetzt. Dabei können die Tageswerte auch gewichtet werden, wobei die Gewichtungsstruktur einer abnehmenden geometrischen Reihe folgt. Die Abbildung „Integriertes Macro-Finance-Dynamics-Modell“ zeigt einen Simulationslauf des integrierten Modells. Für den Gütermarkt werden dabei nur BRE unterstellt. Die Abbildung zeigt die hohe Volatilität von Output, Inflationsrate und stock price, außerdem Konfidenzbänder (gestrichelte Linien), die unter BRE auftreten. Insbesondere lassen sich mit einem solchen Modell das Entstehen und das Platzen von Blasen auf dem Finanzmarkt und die daraus resultierenden realwirtschaftlichen Auswirkungen abbilden.
Das integrierte Finanzmarkt-Realmarkt-Modell lässt sich auch aus geldpolitischer Sicht auswerten, indem nach der optimalen zinspolitischen Reaktion auf Schocks im Rahmen dieses Modells gefragt wird. In einem Modell mit BRE, die im Kern zurückblickend sind, geht die Eigenschaft der history dependence der optimalen unrestringierten Geldpolitik unter Commitment (die im Fall vorausschauender RE gilt) verloren (Neukeynesianische Makroökonomik, optimale geldpolitische Reaktion); vielmehr gilt der Grundsatz, dass je zurückblickender die privaten Agenten sind, desto vorausschauender sollten optimale Zinsregeln vom Taylor-Typ sein; anderenfalls verliert die Eigenschaft der Stabilisatorwirkung von Taylor-Regeln ihre Gültigkeit. In einem um den Finanzmarkt erweiterten NKM-Modell kann man zusätzlich zur geldpolitischen Zielsetzung des flexible inflation targeting (d.h. der Minimierung der gewichteten Summe der Inflations- und Outputlückenvarianz) ein Finanzstabilitätsziel (Minimierung der Stock-Price-Varianz) in der Verlustfunktion der Zentralbank berücksichtigen. Wird dann eine konventionelle Geldpolitik (im Sinne einer Standard-Taylor-Regel) betrieben, nimmt der Gesamtverlust im Vergleich zum flexible inflation targeting zu, jedoch verringert er sich, wenn die Zentralbank neben der Zinspolitik zusätzlich eine optimale unkonventionelle Geldpolitik (i.S. des Ankaufs bzw. Verkaufs von Assets) auf dem Finanzmarkt betreibt und sich bei ihren Kaufentscheidungen an der Stock-Price-Lücke, d.h. der Differenz zwischen aktuellem und Fundamentalwert ausrichtet.
c) Grundsätzlich lassen sich im NKM-Modell mit BRE weitere Heterogenitäten mit aufnehmen, die sich insbesondere auf das Konsumverhalten der privaten Haushalte und Preissetzungsverhalten der Unternehmen beziehen, sodass sich im Endergebnis ein echtes ACE-Modell (Agent-Based Computational Economics-Modell) ergibt (Agent-based-Modelle). Bspw. kann man bei den Haushalten zwischen Vermögensbesitzern und Wirtschaftssubjekten, die als einzige Einkommensquelle nur Lohneinkommen zur Verfügung haben, unterscheiden. Man erhält dann einzelwirtschaftliche Konsumfunktionen, die realzins- bzw. einkommensabhängig sind, sodass sich gesamtwirtschaftlich gesehen eine Konsumnachfrage ergibt, die vom Realzins und Einkommen abhängig ist. Ebenso kann man bei der Preissetzung der Unternehmen zwischen Wirtschaftssubjekten unterscheiden, die ihre Preise in Abhängigkeit der zukünftigen Grenzkosten setzen und solchen, die aufgrund von Preisindexierung oder Anpassungskosten eher zurückblickend sind. Weiter kann berücksichtigt werden, dass das Konsum- oder Preissetzungsverhalten auch vom entsprechenden Verhalten anderer Wirtschaftssubjekte beeinflusst wird (wie zum Beispiel external habit formation im Konsum). Darüber hinaus ist in ACE-Ansätzen die grundlegende Annahme allgemeiner Gleichgewichtsmodelle (DSGE-Modelle), wonach sich der Gütermarkt stets im Zustand des Gleichgewichts befindet, zu modifizieren, da jetzt auf das Verhalten einzelner Wirtschaftssubjekte und die Interaktionen, die zwischen ihnen bestehen, abgestellt wird, sodass im Rahmen einer solchen Bottom-up-Perspektive gesamtwirtschaftlich gesehen kein Gleichgewicht auf dem Gütermarkt mehr bestehen muss. Vielmehr muss sich dieses endogen durch die Interaktionen der Agenten (die sich als Matching-Prozess darstellen lassen) ergeben. In entsprechender Weise ist auch das Verhalten der Agenten auf dem Arbeitsmarkt (der im NKM-Grundmodell nur implizit bei der Mikrofundierung eine Rolle spielt und wie ein vollkommener Markt behandelt wird) zu modellieren. Das NKM-Modell mit BRE lässt sich in vielfältiger Weise zu einem ACE-Modell erweitern, allerdings gibt es diesbezüglich zwar zahlreiche Ansätze, aber noch kein allgemein akzeptiertes Konsensmodell.
Vgl. auch Agent-based-Modelle.
Abbildung: „Integriertes Macro-Finance-Dynamics-Modell“
Vgl. zugehöriger Schwerpunktbeitrag Neukeynesianische Makroökonomik.
Zeitschriften
Literaturhinweise SpringerProfessional.de
Bücher auf springer.com
Interne Verweise
Neukeynesianisches Grundmodell mit begrenzter Rationalität
Neukeynesianisches Grundmodell mit begrenzter Rationalität
- Agent-Based Computational Economics
- Agent-Based Computational Economics
- Agent-Based-Modelle
- Agent-Based-Modelle
- Akzelerator
- Animal Spirits
- Discrete-Choice-Theory
- Discrete-Choice-Theory
- DSGE-Modelle
- DSGE-Modelle
- Erwartung
- Euler-Gleichung des Konsums
- Finanzmarkttheoretische Ansätze
- Finanzmarkttheoretische Ansätze
- Finanzmarkttheoretische Ansätze
- flexible inflation targeting
- Geldpolitik
- hybride Systeme
- Impuls-Antwort-Folgen
- Impuls-Antwort-Folgen
- Macro-Finance Dynamics
- Macro-Finance Dynamics
- Neukeynesianische Makroökonomik
- Neukeynesianische Makroökonomik, dynamisches Grundmodell
- Neukeynesianische Makroökonomik, dynamisches Grundmodell
- Neukeynesianische Makroökonomik, dynamisches Grundmodell
- Neukeynesianische Makroökonomik, dynamisches Grundmodell
- Neukeynesianische Makroökonomik, optimale geldpolitische Reaktion
- Phillips-Kurve
- Sentiment Dynamics
- Stagflation
- Subprime-Krise
- Switching Dynamics
- Switching Dynamics
- Switching Dynamics
- Zinsregel vom Taylor-Typ
- Zustandsgleichungen
- Zustandsgleichungen