Neukeynesianische Makroökonomik, dynamisches Grundmodell
Übersicht
zuletzt besuchte Definitionen...
1. Charakterisierung: Das dynamische Grundmodell der Neukeynesianischen Makroökonomik ist ein sog. vorausschauendes makroökonomisches System, das sowohl nachfrage- als auch angebotsseitig durch rationale Zukunftserwartungen gekennzeichnet ist. Die Nachfrageseite wird durch eine dynamische, realzinsabhängige IS-Gleichung beschrieben, die aus der Euler-Gleichung des Konsums resultiert, während die Angebotsseite durch eine neukeynesianische Phillips-Kurve charakterisiert wird. In der IS-Gleichung wird üblicherweise die Outputvariable durch die Outputlücke
mit dem Flexpreis-Outputniveau
ersetzt. Bei konstanter Technologie kann dabei das Outputniveau bei völliger Preisflexibilität (
) wie eine exogene Variable aufgefasst werden. Die beiden Modellgleichungen lauten dann
mit xt = Outputlücke, πt = Inflationsrate, it = Nominalzins, Et = rationaler Erwartungsoperator, . Von der Mikrofundierung (optimale Preissetzung einer monopolistischen Unternehmung bei Vorliegen nominaler Rigiditäten) hängt die Steigung
der Phillips-Kurve negativ vom Grad der Preisrigidität sowie positiv von der Inversen der intertemporalen Substitutionselastizität des Konsums
sowie der inversen Arbeitsangebotselastizität ab.
ut und kt sind Störvariablen, die einen Nachfrage- bzw. Kostenschock kennzeichnen. Dabei wird typischerweise unterstellt, dass es sich um temporäre Schocks handelt, die einem autoregressiven Prozess erster Ordnung folgen. Im Unterschied zu traditionellen keynesianischen Totalmodellen (makroökonomische Totalmodelle geschlossener Volkswirtschaften, Totalmodelle offener Volkswirtschaften) wird anstelle der Geldmenge der Nominalzins it als geldpolitisches Steuerungsinstrument angesehen. Da dieser bereits in der IS-Gleichung (1) auftritt, kann auf eine eigenständige Geldmarktgleichung (LM-Gleichung) verzichtet werden. Für die geldpolitische Instrumentvariable it wird unterstellt, dass diese einer Regelbindung vom Taylor-Typ folgt. Dabei wird der Zins gemäß J.B. Taylor (1993, 1999) in linearer Weise an die Inflations- und Outputlücke gekoppelt:
Mit i* und werden angestrebte Zielwerte von
und
bezeichnet. In numerischen Simulationen werden diese der Einfachheit halber gleich null gesetzt. In der Zinsregel charakterisiert die Größe
einen Zinsschock, der im Grundmodell der Neukeynesianischen Makroökonomik dann von Relevanz ist, wenn die intertemporalen Wirkungen von monetären Schocks auf die vorausschauenden Variablen xt und
untersucht werden sollen. Für die positiven Koeffizienten
und
in (3) wird üblicherweise
unterstellt, sodass dem Inflationsziel ein stärkeres Gewicht als dem Outputziel beigemessen wird. Weiter wird für den Koeffizienten
das Taylor-Prinzip
angenommen. Eine Steigerung der Inflationsrate, die durch einen expansiven Nachfrageschock erzeugt wird, bewirkt dann gemäß
(3) eine im Vergleich dazu überproportionale Erhöhung des Nominalzinses, sodass auch der Realzins zunimmt, was sich wiederum dämpfend auf die Güternachfrage und die Inflationsrate auswirkt. Die Annahme ist damit gleichzeitig eine Stabilitätsbedingung. Sie stellt insbesondere sicher, dass die Zustandsgleichungen des neukeynesianischen Grundmodells, welche vollständig das dynamische Verhalten dieses Systems beschreiben, die Eigenschaft der Sattelpunktstabilität aufweisen. Setzt man die Zinsregel (3) (mit
) in die IS-Gleichung (1) ein, ergibt sich für die Zustandsgleichungen die matrizielle Darstellung
wobei
Bei Gültigkeit des Taylor-Prinzips hat die Systemmatrix zwei instabile Eigenwerte, d.h. zwei Lösungen
und
der charakteristischen oder quadratischen Gleichung in
(wobei det = Determinante und I2,2 = - Einheitsmatrix), welche außerhalb des Einheitskreises liegen. Diesen beiden Eigenwerten stehen die beiden Sprungvariablen oder vorausschauenden Variablen
und
gegenüber, sodass sich nach den Stabilitätsbedingungen von Blanchard und Kahn (1980) als Folge realer oder monetärer Schocks jeweils eindeutig bestimmte konvergente Anpassungsprozesse für die modellendogenen Variablen
,
,
und
ergeben. Algebraisch können diese über die sog. Vorwärtslösung des Differenzengleichungssystems (4) ermittelt werden. Dabei zeigt sich, dass die Lösungszeitpfade des rein vorausschauenden Systems allein durch die (exogen vorgegebenen) Persistenz- oder Autokorrelationsparameter der Schockvariablen ut,
und kt bestimmt werden, also eine extrinsische Dynamik aufweisen. So gilt bei einem (von den Privaten im Voraus nicht antizipierten) stochastischen Kostenschock, der einem autoregressiven Prozess erster Ordnung mit dem Autokorrelationsparameter
folgt, die Lösungsdarstellung für die Zustandsvariablen xt und
:
Wegen werden durch (7) konvergente Anpassungszeitpfade beschrieben, die langfristig gegen den Anfangs-Steady-State
konvergieren.
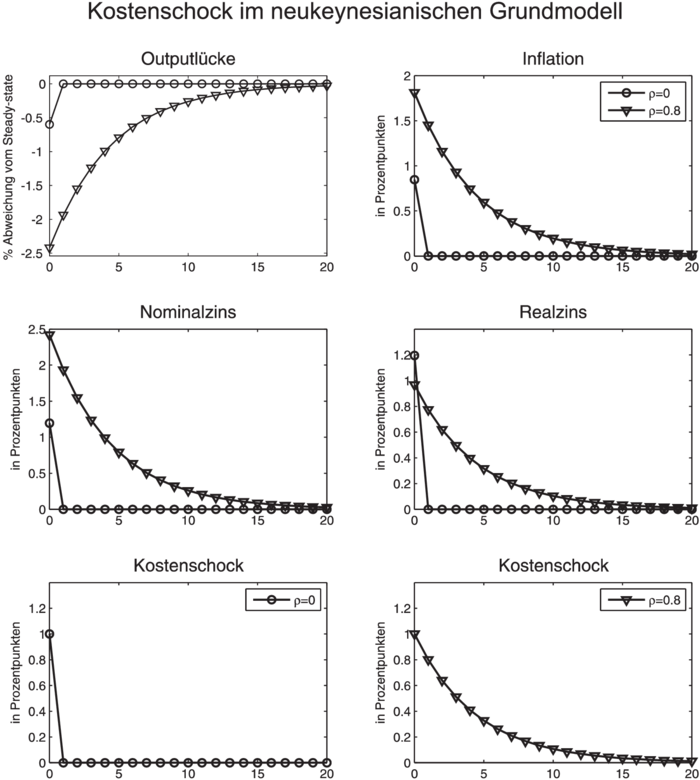
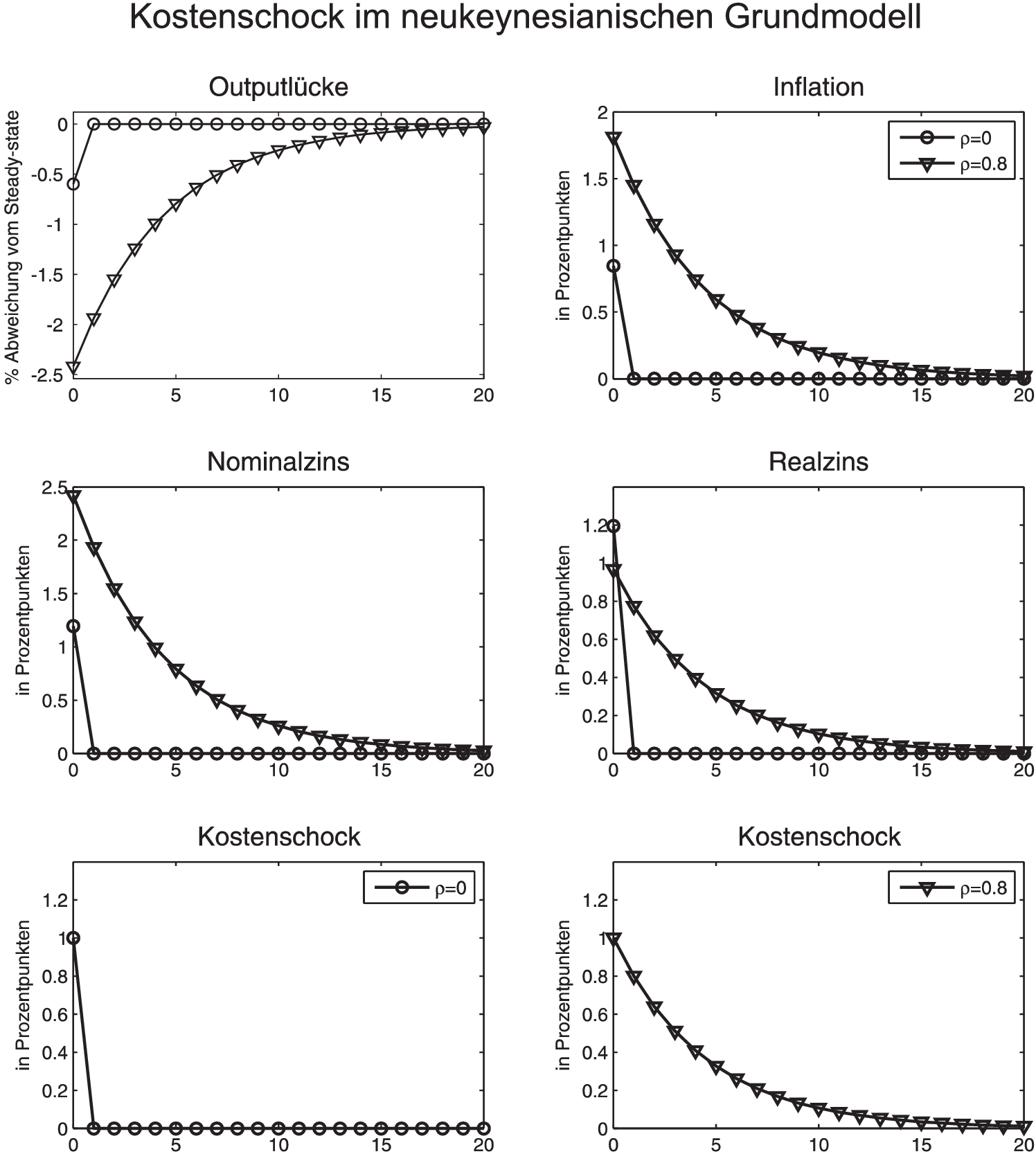
2. Wirkungen eines Kostenschocks: Die intertemporalen Wirkungen eines temporären Kostenschocks werden durch die Abbildung „Kostenschock im neukeynesianischen Grundmodell” veranschaulicht. Der Schock tritt im Zeitpunkt auf und entwickelt sich gemäß der Exponentialfunktion
,
sodass er im Fall langfristig verschwindet, d.h. in das Nullniveau zurückkehrt. Im Sonderfall, dass der Schock keine Persistenz aufweist (
), besteht sein Anpassungsprozess nur aus zwei Perioden. Gemäß der Lösungsdarstellung (7) beträgt dann die Anpassung der modellendogenen Variablen im Fall
ebenfalls nur aus zwei Perioden. Der Kostenschock erzeugt temporäre Stagflation (Outputsenkung bei gleichzeitiger Inflation), die mit Nominal- und Realzinssteigerungen verbunden ist. Der Kostenschock führt gemäß der Phillips-Kurve (2) zu unmittelbarer Inflation und wegen des unterstellten Taylor-Prinzips zu einem im Vergleich dazu stärkeren Anstieg des Nominalzinses, sodass auch der Realzins steigt, was Gegenwartskonsum in die Zukunft verlagert und nach der IS-Gleichung (1) einen Rückgang des Outputs und der Outputlücke induziert. Im Anschluss an die Schockperiode kehren alle Variablen in monotoner Weise in ihre Ausgangsniveaus zurück. – 3. Kritik und Weiterentwicklungen: Die Anpassungsprozesse sind dahingehend zu kritisieren, dass nach den Anfangssprüngen monotone Anpassungsprozesse zurück zum Anfangsgleichgewicht stattfinden. Die Abweichungen vom Anfangsgleichgewicht sind bereits in der Anfangsperiode maximal. Realistisch wären dagegen buckelförmige Verläufe, d.h. eine zunächst nur schwache Anfangsreaktion (im Beispiel Stagflation), die sich im Zuge der Anpassung weiter verstärkt, sodass die maximalen Abweichungen vom Anfangs-Steady-State nicht sofort, sondern erst nach einer gewissen Anpassungsdauer eintreten. Erst danach würde es zu einer Abschwächung der Stagflation und der Zinssteigerungen kommen.
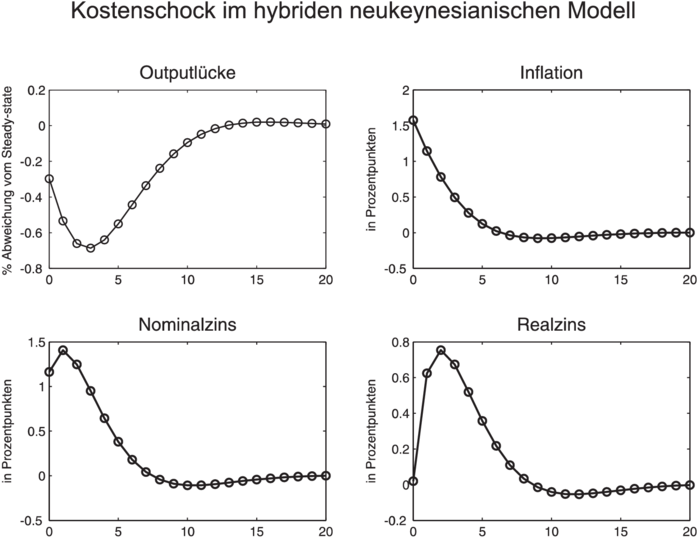
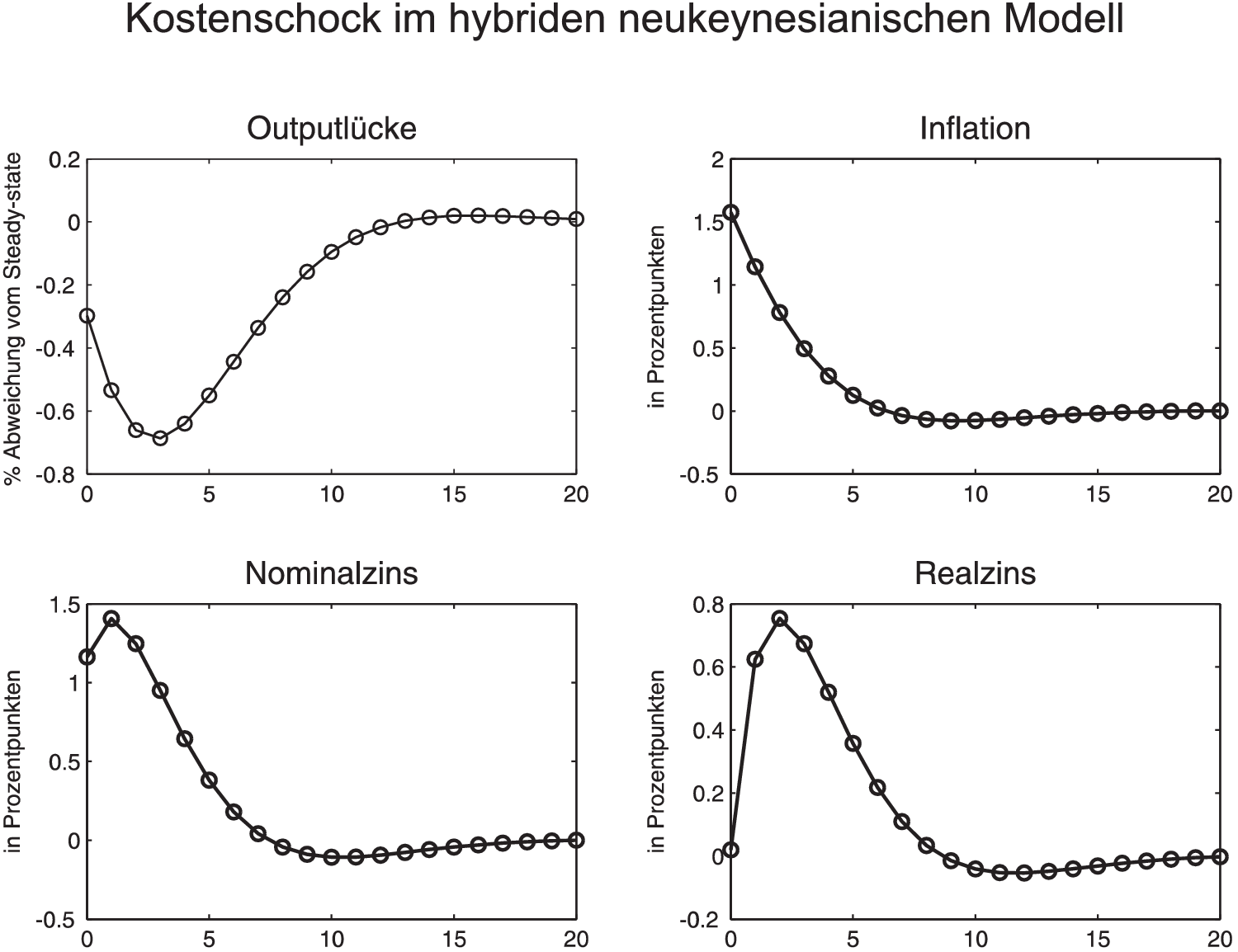
Solche buckelförmigen Anpassungsprozesse lassen sich durch sog. hybride Systeme erzeugen, die in der IS- bzw. Phillips-Kurven-Gleichung neben einem vorausschauenden ( bzw.
) gleichzeitig auch ein analoges zurückblickendes (
bzw.
) Element enthalten. Solche Lag-Terme in (1) bzw. (2) lassen sich mit gewohnheitsmäßigem Konsumverhalten (habit formation) bzw. Daumenregeln (rules of thumb) bei der Preisfestsetzung begründen. Als Folge davon treten in den Zustandsgleichungen dieses erweiterten neukeynesianischen Modells jetzt auch vorherbestimmte Variablen und endogene stabile Eigenwerte auf, die dann zusammen mit den exogenen Persistenzparametern das dynamische Anpassungsverhalten der endogenen Modellvariablen bestimmen. Dieses ist jetzt neben extrinsischer auch durch intrinsische Dynamik gekennzeichnet. Es ergeben sich dann buckelförmige Verläufe, wie durch die Abbildung „Kostenschock im hybriden neukeynesianischen Modell” verdeutlicht werden.
Das dynamische Grundmodell der Neukeynesianischen Makroökonomik lässt sich auch dahingehend kritisieren, dass alle Agenten homogen in der Erwartungsbildung sind, d.h. dass ausschließlich rationale Erwartungen unterstellt werden. Eine Alternative wäre ein Mix aus vorausschauenden (rationalen) und zurückblickenden (autoregressiven) Erwartungen, der dann ebenfalls auf ein hybrides System und buckelförmige Anpassungsprozesse führen würde.
Die zyklische Dynamik und Volatilität im Anpassungsverhalten der modellendogenen Variablen würden sich noch weiter erhöhen, wenn bei den Wirtschaftssubjekten ein Lernverhalten und die Möglichkeit des Wechselns der Erwartungshypothese gemäß der Discrete-Choice-Theory unterstellt werden. Dadurch lassen sich auch die von Keynes betonten Animal Spirits, d.h. der häufige Wechsel von optimistischen zu pessimistischen Stimmungen und die damit verbundenen Schwankungen realer Größen, modelltheoretisch erfassen.
Vgl. zugehöriger Schwerpunktbeitrag Neukeynesianische Makroökonomik.
Bücher
Zeitschriften
Literaturhinweise SpringerProfessional.de
Bücher auf springer.com
Interne Verweise
Neukeynesianische Makroökonomik, dynamisches Grundmodell
- Agent-Based-Modelle
- Angebotsschock
- dynamische Makroökonomik
- Dynamische makroökonomische Systeme
- Dynamisches System
- Eigenwert
- Euler-Gleichung des Konsums
- extrinsische Dynamik
- flexible inflation targeting
- Gap
- gestaffelte Preissetzung
- hybride Systeme
- intrinsische Dynamik
- Neuer Keynesianismus
- Neukeynesianische Makroökonomik
- Neukeynesianische Makroökonomik, optimale geldpolitische Reaktion
- Neukeynesianisches Grundmodell mit begrenzter Rationalität
- Output Gap
- Outputlücke
- Sattelpunktstabilität
- Sentiment Dynamics
- Zinsregel vom Taylor-Typ
- Zustandsgleichungen
Neukeynesianische Makroökonomik, dynamisches Grundmodell
- Animal Spirits
- AR(p)-Prozess
- Discrete-Choice-Theory
- Eigenwert
- Euler-Gleichung des Konsums
- extrinsische Dynamik
- hybride Systeme
- IS-Gleichung
- Lag
- LM-Gleichung
- makroökonomische Totalmodelle geschlossener Volkswirtschaften
- Neukeynesianische Makroökonomik
- Phillips-Kurve
- Sattelpunktstabilität
- Stagflation
- Totalmodelle offener Volkswirtschaften
- Zustandsgleichungen
- Zustandsgleichungen