Normalform

Spieltheorie

Die Normalform (S₁, ..., S_n; u₁, ..., u_n) eines n-Personen-Spiels mit den Spielern 1, ..., n beschreibt ein Spiel rein statisch. Für Spieler i = 1, ..., n bezeichnet S_i = {s_i¹, s_i², s_i³, ... } die Menge seiner Strategien s_i und u_i seine Auszahlungsfunktion. Allen Strategienvektoren s = (s₁, ..., s_n) mit s_i S_i für i = 1, ..., n ordnet die Auszahlungsfunktion u_i kardinale Nutzenwerte u_i(s) zu, die angeben, wie Spieler i die durch s implizierten Ergebnisse bewertet.

Bild in Originalgröße zeigen

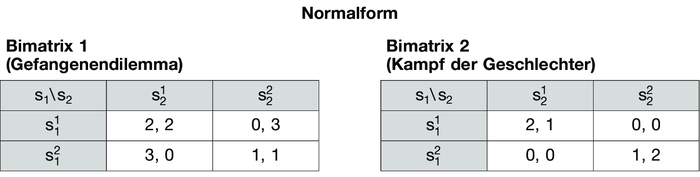
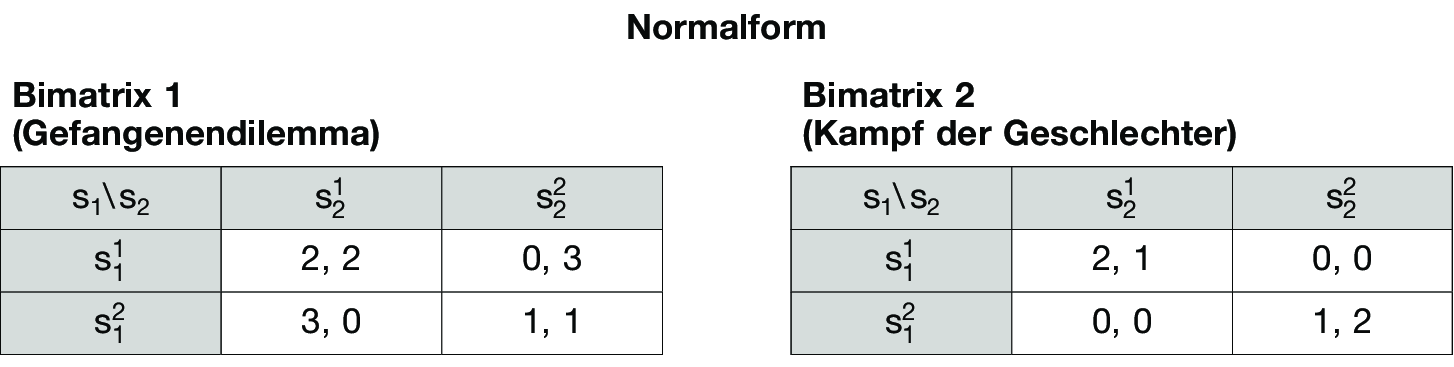
Bekannte Spiele mit zwei Spielern (n = 2), die über jeweils zwei Strategien verfügen, sind das Gefangenendilemma (vgl. Bimatrix 1 in der Abbildung „Normalform”) sowie der Kampf der Geschlechter (vgl. Bimatrix 2 in der Abbildung „Normalform”). Sind Spiele wie die Bimatrixspiele 1 und 2 symmetrisch, so genügt es, wegen u_i(s_i^k, s_j^l) = u_j(s_i^l, s_j^k) nur eine Nutzenbewertung anzugeben. Das Gleiche gilt für die sog. 2-Personen-Nullsummenspiele mit u₁(s) + u₂(s) = 0 für alle Strategievektoren s = (s₁, s₂), da u₂(s) = - u₁(s).

Vgl. auch Spieltheorie.

Wirtschaftsinformatik

1. Begriff: In der Datenorganisation ein Zustand einer Relation (bzw. einer Datei), der i.Allg. durch Normalisierung erzeugt wird.

2. Arten: Man unterscheidet bis zur fünften Normalform. Die Normalformen bauen aufeinander auf; d.h. eine Relation in dritter Normalform ist automatisch auch in zweiter Normalform (und damit auch in erster Normalform) etc.; von praktischer Bedeutung sind  v.a. die Normalformen bis hin zur dritten. Die erste Normalform fordert, dass in Attributen stets nur eine Information gespeichert wird. Die zweite Normalform postuliert die Minimalität des Primärschlüssels einer Relation im Hinblick darauf, dass keine überflüssigen Attribute darin verwendet werden. Über die dritte Normalform werden sog. transitive Abhängigkeiten ausgeschlossen, die dadurch entstehen, dass eine abhängige Relation in eine andere integriert wurde.